三角比の相互関係と値の求め方

こんにちは、リンス(@Lins016)です。
今回は三角比の相互関係と値の求め方について学習していこう。

三角比の相互関係から値を求めよう

三角比の\(\small{ \ \sin \theta \ }\)、\(\small{ \ \ \cos \theta \ }\)、\(\small{ \ \ \tan \theta \ }\) のうち\(\small{ \ 1 \ }\)つの値が与えられていると、相互関係から残りの\(\small{ \ 2 \ }\)つの値を求めることができる。

だから相互関係の式は必ず覚えておかないといけないからね。この単元の中で一番重要な公式って言ってもいいと思う。

でも相互関係の式以外にも余角や補角の関係式もよく利用する式だからきちんと覚えておこう。

三角比の平方の関係式

\(\small{ \ \triangle \mathrm{ABC} \ }\)が\(\small{ \ \angle \mathrm{C}=90^{\circ} \ }\)の直角三角形のとき三平方の定理から\(\small{ \ a^2+b^2=c^2 \ }\)が成り立つ。
これを両辺\(\small{ \ c^2 \ }\)で割ると\(\small{ \ \left(\displaystyle \frac{a}{c}\right)^2+\left(\displaystyle \frac{b}{c}\right)^2=1 \ }\)
\(\small{ \ \sin \theta=\displaystyle \frac{a}{c} \ }\)、\(\small{ \ \cos \theta=\displaystyle \frac{b}{c} \ }\)だから\(\small{ \ \sin^2 \theta +\cos^2 \theta=1 \ }\)が成り立つよね。
この式の両辺を\(\small{ \ \cos^2 \theta \ }\)で割ると、\(\small{ \ 1+ \tan^2 \theta =\displaystyle \frac{1}{\cos^2 \theta} \ }\)が導ける。
また、両辺を\(\small{ \ \sin^2 \theta \ }\)で割ると\(\small{ \ 1+\displaystyle \frac{1}{\tan^2 \theta}=\displaystyle \frac{1}{\sin^2 \theta} \ }\)が導けるよね。

三角比の余角の関係式

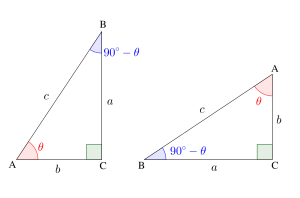
\(\small{ \ \triangle\mathrm{ABC} \ }\)が\(\small{ \ \angle \mathrm{C}=90^{\circ} \ }\)の直角三角形のとき、\(\small{ \ \angle \mathrm{A}=\theta \ }\)とすると、\(\small{ \ \angle \mathrm{B}=90^{\circ}-\theta \ }\)になるよね。

だから回転させた三角形と元の三角形を比較することで余角\(\small{ \ (90^{\circ}-\theta) \ }\)の関係式を求めることができるんだ。
\(\small{ \ \displaystyle \frac{a}{c}=\sin \theta=\cos (90^{\circ}-\theta) \ }\)
\(\small{ \ \displaystyle \frac{b}{c}=\cos \theta=\sin (90^{\circ}-\theta) \ }\)
\(\small{ \ \displaystyle \frac{a}{b}=\tan \theta=\displaystyle \frac{1}{\tan (90^{\circ}-\theta)} \ }\)

三角比の補角の関係式

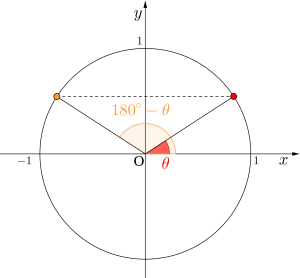
単位円を書いて\(\small{ \ \theta \ }\)と\(\small{ \ 180^{\circ}-\theta \ }\)の位置を比較してみよう。
図から
\(\small{ \ \sin(180^{\circ}-\theta)=\sin \theta \ }\)
\(\small{ \ \cos(180^{\circ}-\theta)=-\cos \theta \ }\)
\(\small{ \ \tan(180^{\circ}-\theta)=-\tan \theta \ }\)
がいえるよね。

数学Ⅱの三角関数で加法定理って公式を覚えるんだけど、この公式を覚えてしまって、余角や補角はこれを使って値を求めてもいいよ。

加法定理を使わずにきちんと覚えられればいいけど、たまにしか出てこない式って忘れちゃうから、なかなか覚えられなかったりするんだ。

それだったら加法定理を覚えてそれに代入してほうがいい。数学Ⅱの三角関数では加法定理を覚えてなかったら、ほぼ\(\small{ \ 0 \ }\)点だからね。必ず覚えないといけない式なんだ。

\(\small{ \ \sin(90^{\circ}-\theta)=\sin90^{\circ}\cos \theta+\cos90^{\circ}\sin \theta=\cos \theta \ }\)

三角比の逆数の関係式

この式はほとんど使うこともないけど、せっかくだから一応書いておくね。

三角比っていうのは全部で\(\small{ \ 6 \ }\)つの比があって、高校数学では正弦、余弦、正接の\(\small{ \ 3 \ }\)つを学習するんだけど、それ以外にも\(\small{ \ 3 \ }\)つの比が定義されているんだ。

余割\(\small{ \ \csc \theta=\displaystyle \frac{1}{\sin \theta} \ }\)
正割\(\small{ \ \sec \theta=\displaystyle \frac{1}{\cos \theta} \ }\)
余接\(\small{ \ \cot \theta=\displaystyle \frac{1}{\tan \theta} \ }\)

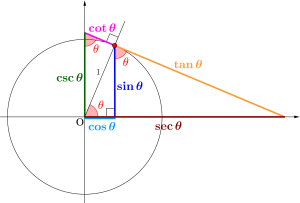
高校数学では出てこないけど、大学で数学を勉強すると出てくるから、大学で数学を勉強するって人は一応こんな値もあるってことを知っておこう。

三角比の値の求め方

三角比のうち\(\small{ \ 1 \ }\)つの値が与えられているとき、残りの値を相互関係から求めることができる。ただ、相互関係の二乗の式を利用するから、求めた答えには正負の\(\small{ \ 2 \ }\)通りの答えが出る。

だから\(\small{ \ \theta \ }\)の範囲に注意して答えを求めよう。

①\(\small{ \ \sin \theta \ }\)か\(\small{ \ \cos \theta \ }\)が与えられてるとき
このときは最初に\(\small{ \ \sin^2 \theta +\cos^2 \theta=1 \ }\)を使って、次に\(\small{ \ \tan\theta =\displaystyle \frac{\sin \theta}{\cos \theta} \ }\)から\(\small{ \ \tan \theta \ }\)を求めよう。

②\(\small{ \ \tan \theta \ }\)が与えられてるとき
このときは最初に\(\small{ \ 1+ \tan^2 \theta =\displaystyle \frac{1}{\cos^2 \theta} \ }\)から\(\small{ \ \cos \theta \ }\)を求めて、\(\small{ \ \tan\theta =\displaystyle \frac{\sin \theta}{\cos \theta} \ }\)から\(\small{ \ \sin \theta \ }\)を求めよう。

この手順を常に守って\(\small{ \ 3 \ }\)つの三角比を求めよう。

\(\small{ \ \sin \theta \ }\)が根号を含まない分数の場合、\(\small{ \ \cos \theta \ }\)を求めるときは次のように計算しよう。
\(\small{\begin{eqnarray} \ \cos \theta&=&\sqrt{1-\sin^2 \theta}\\
&=&\sqrt{1-\left(\displaystyle \frac{a}{b}\right)^2}\\
&=&\displaystyle \frac{\sqrt{b^2-a^2}}{b}\\
&=&\displaystyle \frac{\sqrt{(b-a)(b+a)}}{b} \ \end{eqnarray}}\)
こうすることで、\(\small{ \ 2 \ }\)乗の計算をしなくてすむし、\(\small{ \ (b-a)(b+a) \ }\)は因数分解されてるから、根号の外に括り出せる数も見つけやすいよね。

Point　三角比の相互関係と値の求め方

①相互関係の式はきちんと覚えておこう
②三角比の求め方や余角や補角の求め方をきちんと押さえておこう