こんにちは、リンス(@Lins016)です。
今回は三角関数のグラフ(2)\(\small{ \ y=\tan x \ }\)の形のグラフについて学習していこう。
三角関数のグラフのポイント
これは前回学習した三角関数のグラフ(1)と同じで、\(\small{ \ \tan x \ }\)のグラフも押さえるべきポイントがあるんだ。
それは波の周期と平行移動の二つ。実際は振幅もあるけど、\(\small{ \ \tan \ }\)のグラフだと振幅はグラフにうまく書きづらい。
だから周期と平行移動の二つをきちんと理解していればグラフを書いたり、読み取ったりすることが簡単にできるから、今回の勉強でしっかりと押さえておこう。
\(\small{ \ y=\tan x \ }\)のグラフ
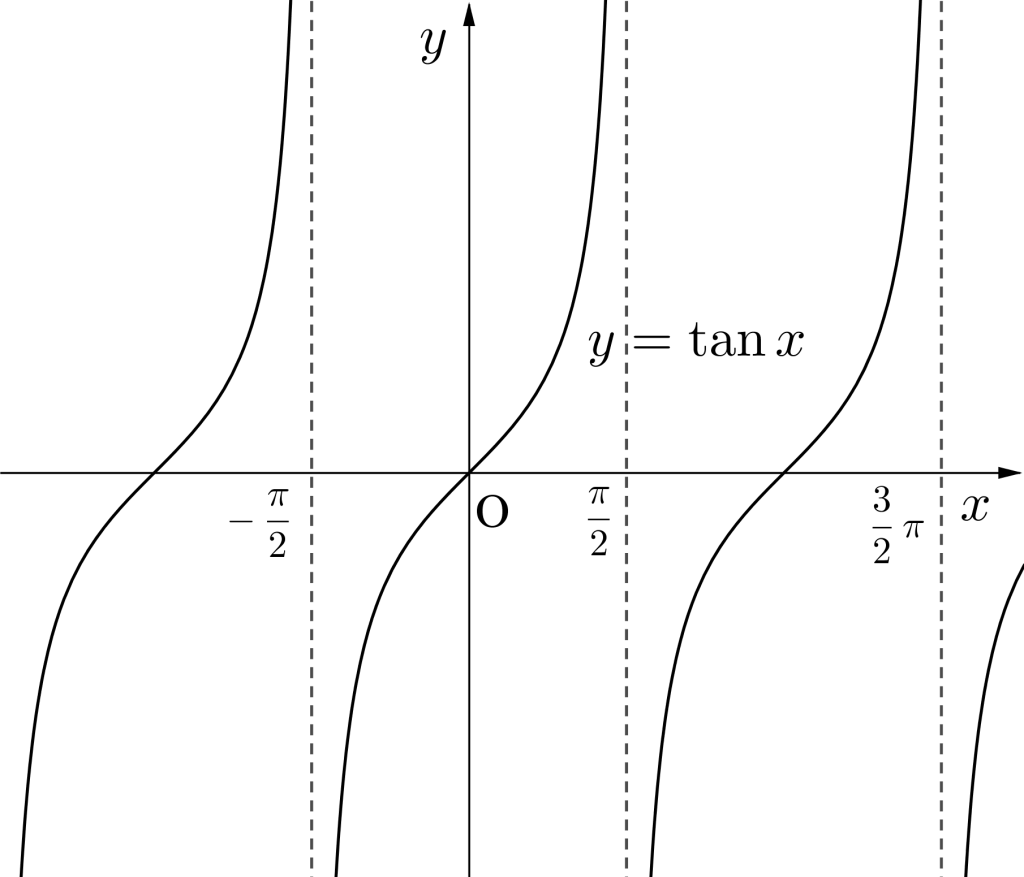
各値とグラフの関係
今回学習するのは\(\small{y=\mathrm{A}\tan k(x-\alpha)+\beta}\)のグラフ。
\(\small{ \ A, \ k, \ \alpha, \ \beta \ }\)の値によってグラフがどのように変化するのか考えてみよう。
グラフ(波)の周期と漸近線
\(\small{ \ y=\tan x \ }\)のグラフは\(\small{ \ x=\displaystyle\frac{\pi}{2}+n\pi \ }\)(\(\small{ \ n \ }\)は整数)の値は存在しないよね。
この\(\small{ \ x=\displaystyle\frac{\pi}{2}+n\pi \ }\)(\(\small{ \ n \ }\)は整数)が漸近線になることを覚えておこう。
\(\small{ \ y=\sin x \ }\)や\(\small{ \ y=\cos x \ }\)のグラフに漸近線は存在しないけど、\(\small{ \ y=\tan x \ }\)のグラフには存在するからね。
\(\small{ \ y=\tan x \ }\)の場合、漸近線の間隔が\(\small{ \ \pi \ }\)で、これが周期になる。
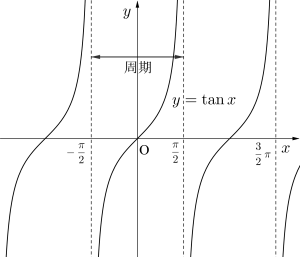
\(\small{ \ y=\tan 2x \ }\)の場合、\(\small{ \ 2x=\displaystyle\frac{\pi}{2}+n\pi \ }\)(\(\small{ \ n \ }\)は整数)の値は存在しないから、\(\small{ \ x=\displaystyle\frac{\pi}{4}+\displaystyle\frac{n\pi}{2} \ }\)(\(\small{ \ n \ }\)は整数)が漸近線になる。
つまり漸近線の間隔の\(\small{ \ \displaystyle\frac{\pi}{2} \ }\)が周期になる。
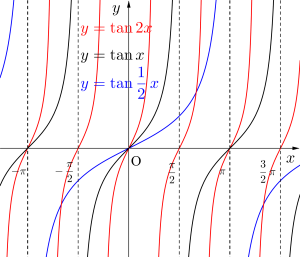
これを一般化すると\(\small{ \ y=\tan kx \ }\)の場合、漸近線は\(\small{ \ kx=\displaystyle\frac{\pi}{2}+n\pi \ }\)を解いた、\(\small{ \ x=\displaystyle\frac{\pi}{2k}+\displaystyle\frac{n\pi}{k} \ }\)(\(\small{ \ n \ }\)は整数)で、周期は\(\small{ \ x=\displaystyle\frac{\pi}{2k}+\displaystyle\frac{n\pi}{k} \ }\)の\(\small{ \ n \ }\)の係数\(\small{ \ \displaystyle\frac{\pi}{k} \ }\)になる。
\(\small{ \ y=\tan x \ }\)のグラフを書く時はまず漸近線から考えるようにしよう。
グラフの平行移動
平行移動は他の関数と同じで、\(\small{ \ x \ }\)を\(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)を\(\small{ \ y-\beta \ }\)に変更することで、\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動したグラフになる。
だから\(\small{ \ y= \mathrm{A}\tan x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ +\alpha \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +\beta \ }\)平行移動したグラフは\(\small{ \ y-\beta= \mathrm{A}\tan(x-\alpha) \ }\)になるからね。

ただ、注意しておきたいのが、前回学習したのと同様に\(\small{ \ y=\tan\left(2x- \displaystyle \frac{\pi}{3}\right) \ }\)のグラフ。
これは\(\small{ \ y=\tan2x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に \(\small{ \ \displaystyle \frac{\pi}{3} \ }\)平行移動したグラフって言いたくなるけど違うからね。
\(\small{ \ y=\tan2\left(x- \displaystyle \frac{\pi}{6}\right) \ }\)って変形して、\(\small{ \ y=\tan2x \ }\)のグラフを\(\small{ \ x \ }\)軸方向に\(\small{ \ \displaystyle \frac{\pi}{6} \ }\)平行移動したグラフってことになるからね。
三角関数グラフの書き方まとめ
\(\small{y=\mathrm{A}\tan k(x-\alpha)+\beta}\)のとき、
・\(\small{ \ k(x-\alpha)=\displaystyle\frac{\pi}{2}+n\pi \ }\)から漸近線を求める
・\(\small{ \ \alpha、\beta \ }\)は平行移動
になるからね。
\(\small{ \ y=\tan \left(\displaystyle\frac{2}{3}x-\displaystyle\frac{\pi}{2}\right) \ }\)のグラフを書け。
\(\small{\begin{eqnarray} \ y&=&\tan \left(\displaystyle\frac{2}{3}x-\displaystyle\frac{\pi}{2}\right)\\[5pt]
&=&\tan \displaystyle\frac{2}{3}\left(x-\displaystyle\frac{3}{4}\pi\right) \ \end{eqnarray}}\)
つまり\(\small{ \ y=\tan \displaystyle\frac{2}{3}x \ }\)を\(\small{ \ \displaystyle\frac{3}{4}\pi \ }\)平行移動したグラフ。
また、
\(\small{ \ \displaystyle\frac{2}{3}x-\displaystyle\frac{\pi}{2}=\displaystyle\frac{\pi}{2}+n\pi \ }\)(\(\small{ \ n \ }\)は整数)
これを解くと
\(\small{ \ x=\displaystyle\frac{3}{2}(n+1)\pi \ }\)(\(\small{ \ n \ }\)は整数)
よって漸近線は
\(\small{ \ n=-2 \ }\)のとき、\(\small{ \ x=-\displaystyle\frac{3}{2}\pi \ }\)
\(\small{ \ n=-1 \ }\)のとき、\(\small{ \ x=0 \ }\)
\(\small{ \ n=+1 \ }\)のとき、\(\small{ \ x=\displaystyle\frac{3}{2}\pi \ }\)
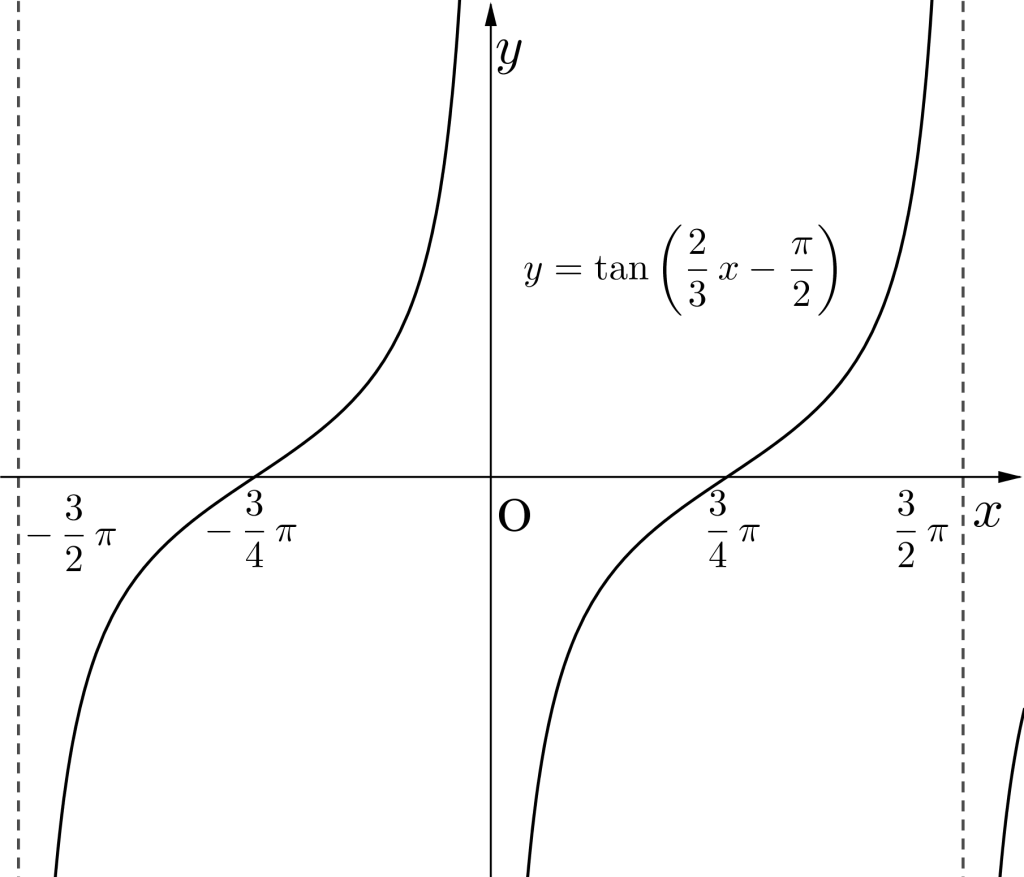

Point 三角関数のグラフ(2)
①\(\small{ \ \tan \ }\)のグラフは周期・平行移動に注意しよう
②周期は漸近線を調べて求めよう

