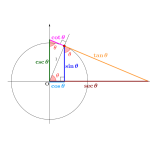
こんにちは、リンス(@Lins016)です。
今回は三角関数の性質の公式について学習していきましょう。
三角関数の性質の公式
三角関数は覚える公式が多すぎてホント嫌になるよね。
でもたくさん公式が教科書に出てくるけど、そんなにたくさん覚える必要があるかっていうとそんなことないんだ。
覚えるべきものだけしっかりと覚えてしまえばいいから、教科書に書いてある公式を全て暗記しなくてもいいからね。
たくさん覚えられてればいいけど、時間がたつと忘れちゃったりするからね。
最低限のものだけきちんと覚えるようにしよう。
今回はその最低限のものが何かってところも学習していくよ。
・三角関数の相互式
\(\small{ \ \sin^2\theta+\cos^2\theta=1 \ }\)
\(\small{ \ \displaystyle\frac{\sin\theta}{\cos\theta}=\tan\theta \ }\)
\(\small{ \ \tan^2\theta+1=\displaystyle\frac{1}{\cos^2\theta} \ }\)
・\(\small{ \ -\theta \ }\)
\(\small{ \ \sin(-\theta)=-\sin\theta \ }\)
\(\small{ \ \cos(-\theta)=\cos\theta \ }\)
\(\small{ \ \tan(-\theta)=-\tan\theta \ }\)
・\(\small{ \ \theta+\pi \ }\)
\(\small{ \ \sin(\theta+\pi)=-\sin\theta \ }\)
\(\small{ \ \cos(\theta+\pi)=-\cos\theta \ }\)
\(\small{ \ \tan(\theta+\pi)=\tan\theta \ }\)
・\(\small{ \ \pi-\theta \ }\)
\(\small{ \ \sin(\pi-\theta)=\sin\theta \ }\)
\(\small{ \ \cos(\pi-\theta)=-\cos\theta \ }\)
\(\small{ \ \tan(\pi-\theta)=-\tan\theta \ }\)
・\(\small{ \ \displaystyle\frac{\pi}{2}-\theta \ }\)
\(\small{ \ \sin\left(\displaystyle\frac{\pi}{2}-\theta\right)=\cos\theta \ }\)
\(\small{ \ \cos\left(\displaystyle\frac{\pi}{2}-\theta\right)=\sin\theta \ }\)
\(\small{ \ \tan\left(\displaystyle\frac{\pi}{2}-\theta\right)=\displaystyle\frac{1}{\tan\theta} \ }\)
・\(\small{ \ \theta+\displaystyle\frac{\pi}{2} \ }\)
\(\small{ \ \sin\left(\theta+\displaystyle\frac{\pi}{2}\right)=\cos\theta \ }\)
\(\small{ \ \cos\left(\theta+\displaystyle\frac{\pi}{2}\right)=-\sin\theta \ }\)
\(\small{ \ \tan\left(\theta+\displaystyle\frac{\pi}{2}\right)=-\displaystyle\frac{1}{\tan\theta} \ }\)
三角関数の相互関係の式
さすがに次の三つの式は重要だからきちんと覚えておこう。
\(\small{ \ \sin^2\theta+\cos^2\theta=1 \ }\)
\(\small{ \ \displaystyle\frac{\sin\theta}{\cos\theta}=\tan\theta \ }\)
\(\small{ \ \tan^2\theta+1=\displaystyle\frac{1}{\cos^2\theta} \ }\)
この式は三角比の相互関係で学習しているから一度チェックしておこう。
-

三角比の相互関係と値の求め方
余角や補角の三角比や三角比の値の求め方について詳しく解説しています。
続きを見る
単位円を利用した性質の確認
単位円を利用して性質を一つずつ確認してみよう。
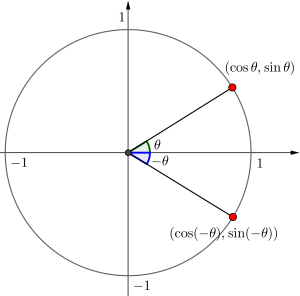
\(\small{ \ -\theta \ }\)を単位円に書き込むと
\(\small{ \ \sin(-\theta)=-\sin\theta \ }\)
\(\small{ \ \cos(-\theta)=\cos\theta \ }\)
になるのが分かるよね。
この二つを利用すると
\(\small{ \ \tan(-\theta)=-\tan\theta \ }\)になるからね。
次に\(\small{ \ \theta+\pi \ }\)を単位円に書き込むと
\(\small{ \ \sin(\theta+\pi)=-\sin\theta \ }\)
\(\small{ \ \cos(\theta+\pi)=-\cos\theta \ }\)
になるのがわかるよね。
この二つの式を利用すると
\(\small{ \ \tan(\theta+\pi)=\tan\theta \ }\)になるからね。

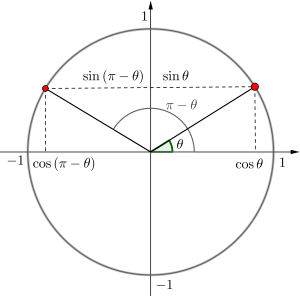
次に\(\small{ \ \pi-\theta \ }\)を単位円に書き込むと
\(\small{ \ \sin(\pi-\theta)=\sin\theta \ }\)
\(\small{ \ \cos(\pi-\theta)=-\cos\theta \ }\)
になるのがわかるよね。
この二つの式を利用すると
\(\small{ \ \tan(\pi-\theta)=-\tan\theta \ }\)になるからね。
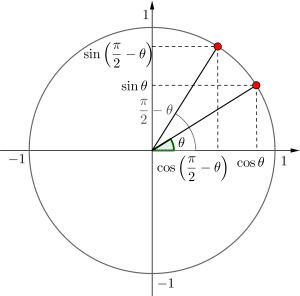
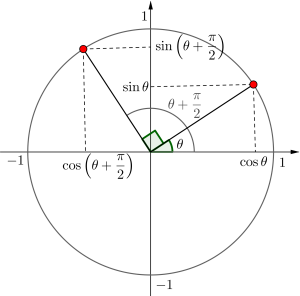
次に\(\small{ \ \displaystyle\frac{\pi}{2}-\theta \ }\)を単位円に書き込むと、少し確認しにくいけど
\(\small{ \ \sin\left(\displaystyle\frac{\pi}{2}-\theta\right)=\cos\theta \ }\)
\(\small{ \ \cos\left(\displaystyle\frac{\pi}{2}-\theta\right)=\sin\theta \ }\)
になるのがわかるよね。
この二つの式を利用して\(\small{ \ \tan\left(\displaystyle\frac{\pi}{2}-\theta\right)=\displaystyle\frac{1}{\tan\theta} \ }\)になるからね。
最後に\(\small{ \ \theta+\displaystyle\frac{\pi}{2} \ }\)を単位円に書き込むと
\(\small{ \ \sin\left(\theta+\displaystyle\frac{\pi}{2}\right)=\cos\theta \ }\)
\(\small{ \ \cos\left(\theta+\displaystyle\frac{\pi}{2}\right)=-\sin\theta \ }\)
になるのがわかるよね。
この二つの式を利用して\(\small{ \ \tan\left(\theta+\displaystyle\frac{\pi}{2}\right)=-\displaystyle\frac{1}{\tan\theta} \ }\)になるからね。
加法定理を利用した公式の確認
ここまで学習して、「たくさん公式覚えてないといけないから大変だな」ってとこから「図形的に考えればなんとかなりそう」って思えるようになったかな。
でも図形的に考えるよりももっと簡単なものがあるんだ。
それは加法定理を利用する方法なんだ。
すでに加法定理の学習が終わっている人は、加法定理をもう覚えているだろうから問題ないよね。
まだ加法定理を覚えていない人は、まず加法定理を覚えよう。
加法定理を覚えてなかったら三角関数のテストでいい点数はとれないからね。
教科書だと加法定理を教わる前にこの三角関数の性質の公式を教わるから、「覚えるの大変だな」ってなるけど、加法定理を覚えていれば、加法定理に代入するだけだからホント簡単。
だからまずは加法定理を覚えよう。
\(\small{ \ \sin\left(\alpha+\beta\right)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \ }\)
\(\small{ \ \cos\left(\alpha+\beta\right)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \ }\)
これを利用すると、例えば
\(\small{ \ \sin\left(\displaystyle\frac{\pi}{2}-\theta\right) \ }\)
\(\small{ \ =\sin\displaystyle\frac{\pi}{2}\cos\theta-\cos\displaystyle\frac{\pi}{2}\sin\theta \ }\)
\(\small{ \ =\cos\theta \ }\)
って導けるからね。
有名角の値と加法定理を覚えてない人は三角関数0点だよって言われても仕方ないぐらい大切な公式だから、これは確実に覚えてね。
めちゃくちゃよく使うからね。
単位円を利用して各値を確認してもいいけど、実際は毎回加法定理で値を求めた方が間違いないと思う。
いちいち単位円書くの面倒だよね。
しかも円がきれいに書けなくて、間違える人もよく見かけるからね。
次の式を簡単にせよ。
(1)
(2)
(3)
(1)
\(\small{ \ =\cos\theta-\cos\theta-\sin\theta-\sin\theta \ }\)
\(\small{ \ =-2\sin\theta \ }\)
(2)
\(\small{ \ =\cos\theta\left(-\cos\theta\right)-\left(-\sin\theta\right)\left(-\sin\theta\right) \ }\)
\(\small{ \ =-1 \ }\)
(3)
\(\small{ \ =-\tan\theta-\displaystyle \frac{1}{\tan\theta}+\tan\theta+\displaystyle \frac{1}{\tan\theta} \ }\)
\(\small{ \ =0 \ }\)

\(\small{ \ \displaystyle \frac{\pi}{2} \ }\)や\(\small{ \ \pi \ }\)とかの\(\small{ \ \sin \ }\)や\(\small{ \ \cos \ }\)の値が\(\small{ \ 0 \ }\)や\(\small{ \ \pm1 \ }\)になるような角が\(\small{ \ \theta \ }\)に足されたり引かれたりしている場合必ず簡単にできるから、まずは簡単にすることを考えよう。
Point 三角関数の性質
①三角関数の性質の公式は加法定理を利用しよう