三角関数と周期関数・偶関数・奇関数

こんにちは、リンス(@Lins016)です。
今回は三角関数と周期関数・偶関数・奇関数について学習していこう。

周期関数と偶関数と奇関数

高校数学で学習する関数（二次関数・指数関数・対数関数・三角関数・分数関数など）で周期関数になるのは三角関数だけなんだ。まあ無理やり作れば、ガウス記号を利用した\(\small{ \ y=x-[x] \ }\)ってのもあるけどね。すごく重要っていうわけじゃないけど、周期関数がどういうものかきちんと押さえておこう。それに合わせて偶関数や奇関数の性質も学習しておこう。

三角関数の方程式

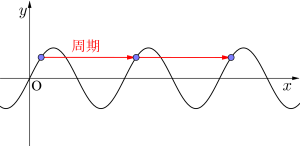
・周期関数
\(\small{ \ f(x+p)=f(x) \ }\)

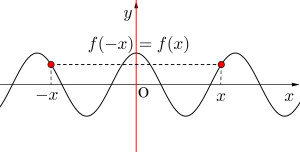
・偶関数
\(\small{ \ f(-x)=f(x) \ }\)

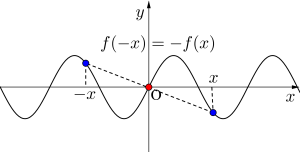
・奇関数
\(\small{ \ f(-x)=-f(x) \ }\)

周期関数

周期関数とは「一定の間隔あるいは周期ごとに取る値が繰り返す関数」のことで、周期を\(\small{ \ p \ }\)とすると周期関数は\(\small{ \ f(x+p)=f(x) \ }\)が成り立つんだ。
特に三角関数のグラフは全て周期関数っていえるんだ。

例えば\(\small{ \ y=\sin x \ }\)の周期は\(\small{ \ 2\pi \ }\)だから、\(\small{ \ f(x)=\sin x \ }\)とすると、\(\small{ \ f(x+2\pi)=f(x) \ }\)が成り立つし、\(\small{ \ y=\tan x \ }\)の周期は\(\small{ \ \pi \ }\)だから\(\small{ \ f(x)=\tan x \ }\)とすると、\(\small{ \ f(x+\pi)=f(x) \ }\)が成り立つ。

周期関数のことをきちんと理解しておこう。このあと教わる三角関数の方程式・不等式の理解にも深く関わってくるからね。

ちなみに周期は実は無数にあって\(\small{ \ f(x)=\sin x \ }\)とすると\(\small{ \ f(x+4\pi)=f(x) \ }\)も成り立つよね。これは\(\small{ \ 4\pi \ }\)ごとに同じ値を繰り返すってことになる式だけど、\(\small{ \ 2\pi \ }\)が周期なら、\(\small{ \ 4\pi \ }\)、\(\small{ \ 6\pi \ }\)・・・も周期になるんだ。

つまり周期が\(\small{ \ p \ }\)なら\(\small{ \ 2p \ }\)、\(\small{ \ 3p \ }\)も周期になるってこと。
周期は無数にあるってことがいえる。この無数にある周期のうち一番短い周期のことを基本周期って言って、\(\small{ \ f(x)=\sin x \ }\)なら\(\small{ \ 2\pi \ }\)、\(\small{ \ f(x)=\tan x \ }\)なら\(\small{ \ \pi \ }\)になる。

三角関数の周期については三角関数のグラフで学習したから、忘れていたらもう一度確認しておこう。\(\small{ \ x \ }\)の係数で周期が判定できるからね。

周期が\(\small{ \ p \ }\)の関数と周期が\(\small{ \ q \ }\)の関数を加えた関数も周期関数で、その周期は\(\small{ \ p \ }\)と\(\small{ \ q \ }\)の最小公倍数になるからね。

偶関数

偶関数とは「\(\small{ \ y \ }\)軸対称な関数」のことで\(\small{ \ f(-x)=f(x) \ }\)が成り立つんだ。

三角関数だと\(\small{ \ \cos(-x)=\cos x \ }\)だから\(\small{ \ y=\cos x \ }\)は偶関数になる。

特に整関数だと\(\small{ \ y=x^n \ }\)で\(\small{ \ n \ }\)が偶数だと偶関数になる。これはよく積分の範囲で利用するから覚えておこう。

奇関数

奇関数とは「原点対称な関数」のことで\(\small{ \ f(-x)=-f(x) \ }\)が成り立つんだ。

三角関数だと\(\small{ \ \sin(-x)=-\sin x \ }\)だから\(\small{ \ y=\sin x \ }\)は奇関数になる。
さらに\(\small{ \ \tan(-x)=-\tan x \ }\)だから\(\small{ \ y=\tan x \ }\)も奇関数になるからね。

特に整関数だと\(\small{ \ y=x^n \ }\)で\(\small{ \ n \ }\)が奇数だと奇関数になる。これもよく積分の範囲で利用するから覚えておこう。

偶関数と奇関数の和・差

偶関数同士の和や差、奇関数同士の和や差がどんな関数になるか考えてみよう。

\(\small{ \ h(x)=f(x)+g(x) \ }\)とする。
①偶関数と偶関数
\(\small{ \ f(-x)=f(x), \ g(-x)=g(x) \ }\)のとき
\(\small{\begin{eqnarray} \ h(-x)&=&f(-x)+g(-x)\\
&=&f(x)+g(x)\\
&=&h(x) \ \end{eqnarray}}\)
偶関数同士の和や差は偶関数になる。

②奇関数と奇関数
\(\small{ \ f(-x)=-f(x), \ g(-x)=-g(x) \ }\)のとき
\(\small{\begin{eqnarray} \ h(-x)&=&f(-x)+g(-x)\\
&=&-f(x)-g(x)\\
&=&-h(x) \ \end{eqnarray}}\)
奇関数同士の和や差は奇関数になる。

③偶関数と奇関数
\(\small{ \ f(-x)=f(x), \ g(-x)=-g(x) \ }\)のとき
\(\small{\begin{eqnarray} \ h(-x)&=&f(-x)+g(-x)\\
&=&f(x)-g(x)\\
&\neq& \pm h(x) \ \end{eqnarray}}\)
偶関数と奇関数の和や差は偶関数にも奇関数にもならない。

定数項も偶関数とみなすことができるから、\(\small{ \ y=x^4+x^2+1 \ }\)も偶関数になるからね。

偶関数と奇関数の積

\(\small{ \ h(x)=f(x) \cdot g(x) \ }\)とする。
①偶関数と偶関数
\(\small{ \ f(-x)=f(x), \ g(-x)=g(x) \ }\)のとき
\(\small{\begin{eqnarray} \ h(-x)&=& f(-x) \cdot g(-x)\\
&=&f(x) \cdot g(x)\\
&=&h(x) \ \end{eqnarray}}\)

②奇関数と奇関数
\(\small{ \ f(-x)=-f(x), \ g(-x)=-g(x) \ }\)のとき
\(\small{\begin{eqnarray} \ h(-x)&=&f(-x) \cdot g(-x)\\
&=&\left\{-f(x)\right\} \cdot \left\{-g(x)\right\}\\
&=&f(x) \cdot g(x)\\
&=&h(x) \ \end{eqnarray}}\)

③偶関数と奇関数
\(\small{ \ f(-x)=f(x), \ g(-x)=-g(x) \ }\)のとき
\(\small{\begin{eqnarray} \ h(-x)&=&f(-x) \cdot g(-x)\\
&=&f(x) \cdot \left\{-g(x)\right\}\\
&=&-h(x) \ \end{eqnarray}}\)

つまり偶関数同士、奇関数同士の積は偶関数になるし、偶関数と奇関数の積は奇関数になるってことがわかるよね。

実際は偶関数や奇関数の和・差・積がどの関数になるかってことよりも、関数に\(\small{ \ -x \ }\)を代入して偶関数になるか奇関数になるか確認しよう。それだけで十分だから。

Point 三角関数と周期関数・偶関数・奇関数

①三角関数の周期は\(\small{ \ x \ }\)の係数から判断する
②偶関数・奇関数の判断は\(\small{ \ f(x) \ }\)に\(\small{ \ -x \ }\)を代入して判断する