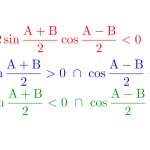こんにちは、リンス(@Lins016)です。
今回は三角方程式・三角不等式と領域について学習していこう。
三角関数を含む方程式不等式と領域
本来領域は数学Ⅱの「不等式と領域」で学習する範囲だけど、三角関数でも領域を図示する問題ってあるんだ。
三角関数が試験範囲の中間テストや期末テストにはそう出題されることはないかもしれないけど、実力テストや入試には出題されるから確実に押さえておこう。
その前にまずは「不等式と領域」を再度確認しておこう。
-

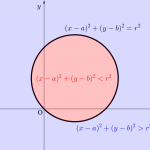
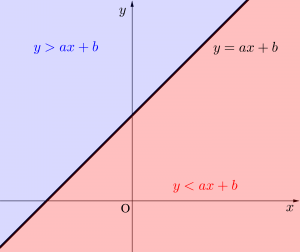
不等式と領域の図示
こんにちは、リンス(@Lins016)です。 今回は不等式と領域の図示について学習していこう。 不等式と領域 \(\small{ \ x \ }\)、\(\small{y \ }\)を含む不等式は、そ ...
続きを見る

図示の問題
「次の条件を満たす点\(\small{ \ \left(x, \ y\right) \ }\)を図示せよ。」って問題があるよね。
図示せよってことで図を書くことに注目しがちだけど、図を書く前に\(\small{ \ x, \ y \ }\)の関係式を求めることが重要なんだ。
\(\small{ \ x, \ y \ }\)の関係式が等式なら円や直線、放物線といった図形になるし、関係式が不等式なら領域になるからね。
つまり図示せよって問題は関係式を求めよって言ってるのと同じだからね。
和積の公式と方程式不等式
以前学習した和積の公式の方程式不等式の解き方では\(\small{ \ x=\pi \ }\)のように\(\small{ \ x \ }\)の値を求めるものだったけど、今回は\(\small{ \ x \ }\)だけじゃなくて\(\small{ \ y \ }\)も含めた方程式不等式になっているから\(\small{ \ x+y=\pi \ }\)のような関係式ができる。
この関係式を図示すればいいんだ。
-

三角関数の合成と和積の公式を利用した三角方程式不等式
合成を利用する場合や和積の公式を利用する場合の見分け方についても詳しく解説しています。
続きを見る
定義域の確認
和積の公式を利用したときに\(\small{ \ \sin\left(x+y\right) \ }\)のように偏角に\(\small{ \ x+y \ }\)のような値が出てくる。\(\small{ \ x, \ y \ }\)に定義域がなかったら\(\small{ \ x+y \ }\)にも定義域はないけど、\(\small{ \ x, \ y \ }\)に定義域があったらどうなるか考えてみよう。
\(\small{ \ 0\leqq x \leqq \pi \ }\)、\(\small{ \ 0\leqq y \leqq \pi \ }\)のとき
\(\small{ \ x+y \ }\)の定義域は\(\small{ \ 0\leqq x+y \leqq 2\pi \ }\)になる。これは\(\small{ \ x, \ y \ }\)ともに最小値のとき最小値になって、\(\small{ \ x, \ y \ }\)ともに最大値のとき最大値になるからなんだ。
\(\small{ \ x-y \ }\)の定義域は\(\small{ \ -\pi\leqq x-y \leqq \pi \ }\)になる。これは\(\small{ \ x \ }\)が最小値で\(\small{ \ y \ }\)が最大値のとき最小値になって、\(\small{ \ x \ }\)が最大値で\(\small{ \ y \ }\)が最小値のとき最大値になるからなんだ。
つまり和の場合は最小値同士・最大値同士を足せばいいし、差の場合は最大値と最小値・最小値と最大値を引けばいいんだ。
ただこれは\(\small{ \ x, \ y \ }\)に関係式がない場合ね。問題文の前提に\(\small{ \ x+2y=\pi \ }\)のような\(\small{ \ x, \ y \ }\)の関係式があったらこれは言えないからね。
関係式があったら\(\small{ \ y=-\displaystyle\frac{1}{2}x+\displaystyle\frac{\pi}{2} \ }\)と\(\small{ \ y \ }\)の定義域\(\small{ \ 0\leqq y \leqq \pi \ }\)を合わせて\(\small{ \ 0\leqq-\displaystyle\frac{1}{2}x+\displaystyle\frac{\pi}{2}\leqq \pi \ }\)から\(\small{ \ x \ }\)の定義域を求めよう。
問題文に\(\small{ \ x, \ y \ }\)の関係式があったら、二つの変数は一つの変数に変えることができるからね。
\(\small{ \ 0\leqq x \leqq 2\pi \ }\),\(\small{ \ 0\leqq y \leqq 2\pi \ }\)のとき、次の条件を満たす点\(\small{ \ \left(x, \ y\right) \ }\)を図示せよ。
(1)\(\small{ \ \cos2x+\cos2y=\cos\left(x+y\right) \ }\)
(2)\(\small{ \ \sin x+\sin y \leqq 0 \ }\)
(1)
\(\small{ \ \cos2x+\cos2y=\cos\left(x+y\right) \ }\)
\(\small{ \ 2\cos\left(x+y\right)\cos\left(x-y\right)=\cos\left(x+y\right) \ }\)
\(\small{ \ \cos\left(x+y\right)\left\{2\cos\left(x-y\right)-1\right\}=0 \ }\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
\cos\left(x+y\right)=0\\
\cos\left(x-y\right)=0
\end{array}
\right.
\end{eqnarray} \ }\)
ここで\(\small{ \ 0\leqq x \leqq 2\pi \ }\),\(\small{ \ 0\leqq y \leqq 2\pi \ }\)より
\(\small{ \ 0\leqq x+y \leqq 4\pi \ }\)、\(\small{ \ -2\pi \leqq x-y \leqq 2\pi \ }\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x+y=\displaystyle\frac{\pi}{2}, \ \displaystyle\frac{3}{2}\pi, \ \displaystyle\frac{5}{2}\pi, \ \displaystyle\frac{7}{2}\pi\\
x-y=-\displaystyle\frac{5}{3}\pi, \ -\displaystyle\frac{\pi}{3}, \ \displaystyle\frac{\pi}{3}, \ \displaystyle\frac{5}{3}\pi
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}
y
=
\begin{cases}
-x+\displaystyle\frac{\pi}{2} \\
-x+\displaystyle\frac{3}{2}\pi\\
-x+\displaystyle\frac{5}{2}\pi\\
-x+\displaystyle\frac{7}{2}\pi\\
x-\displaystyle\frac{5}{3}\pi\\
x-\displaystyle\frac{\pi}{3}\\
x+\displaystyle\frac{\pi}{3}\\
x+\displaystyle\frac{5}{3}\pi\\
\end{cases}
\end{eqnarray} \ }\)
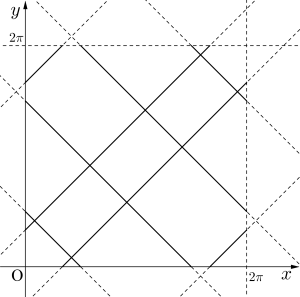
(2)
\(\small{ \ \sin x+\sin y \leqq 0 \ }\)
\(\small{ \ 2\sin\displaystyle\frac{x+y}{2}\cos\displaystyle\frac{x-y}{2}\leqq 0 \ }\)
ここで\(\small{ \ 0\leqq x \leqq 2\pi \ }\),\(\small{ \ 0\leqq y \leqq 2\pi \ }\)より
\(\small{ \ 0\leqq \displaystyle\frac{x+y}{2} \leqq 2\pi \ }\)、\(\small{ \ -\pi \leqq \displaystyle\frac{x-y}{2} \leqq pi \ }\)
(i)\(\small{ \ \sin\displaystyle\frac{x+y}{2}\geqq 0 \ \cap \ \cos\displaystyle\frac{x-y}{2}\geqq0 \ }\)のとき
\(\small{ \ \sin\displaystyle\frac{x+y}{2}\geqq 0 \ }\)より
\(\small{ \ 0\leqq \displaystyle\frac{x+y}{2} \leqq \pi\ }\)
\(\small{ \ \therefore -x\leqq y \leqq x+2\pi \ }\)
\(\small{ \ \cos\displaystyle\frac{x-y}{2}\geqq0 \ }\)より
\(\small{ \ -\displaystyle\frac{\pi}{2}\leqq \displaystyle\frac{x-y}{2} \leqq \displaystyle\frac{\pi}{2} \ }\)
\(\small{ \ \therefore x-\pi\leqq y \leqq x+\pi \ }\)
(ii)\(\small{ \ \sin\displaystyle\frac{x+y}{2}\leqq 0 \ \cap \ \cos\displaystyle\frac{x-y}{2}\leqq0 \ }\)のとき
\(\small{ \ \sin\displaystyle\frac{x+y}{2}\leqq 0 \ }\)より
\(\small{ \ \pi\leqq \displaystyle\frac{x+y}{2} \leqq 2\pi\ }\)
\(\small{ \ \therefore -x+2\pi\leqq y \leqq -x+4\pi \ }\)
\(\small{ \ \cos\displaystyle\frac{x-y}{2}\leqq0 \ }\)より
\(\small{ \ -\pi \leqq \displaystyle\frac{x-y}{2} \leqq -\displaystyle\frac{\pi}{2} \ }\)
\(\small{ \ \displaystyle\frac{\pi}{2}\leqq \displaystyle\frac{x-y}{2} \leqq \pi \ }\)
\(\small{ \ \therefore x-2\pi\leqq y \leqq x-\pi \ }\)
\(\small{ \ x+\pi\leqq y \leqq x+2\pi \ }\)
よって(i)(ii)より図のようになる
ただし境界線は含む。


Point 三角方程式・三角不等式と領域
①図示の問題は図を考える前にまずは関係式を導こう
②定義域に注意して関係式をきれいに整理しよう。
\(\small{ \ 0\leqq x \leqq \pi \ }\),\(\small{ \ 0\leqq y \leqq \pi \ }\)のとき
\(\small{ \ \sin2x+\sin2y=2\sin\left(x+y\right) \ }\)を満たす点\(\small{ \ \left(x, \ y\right) \ }\)を図示せよ。
また、点\(\small{ \ \left(x, \ y\right) \ }\)がこの範囲にあるとき、\(\small{ \ y-\left(x-a\right)^2 \ }\)の最大値を求めよ。
\(\small{ \ \sin2x+\sin2y=\sin\left(x+y\right) \ }\)
\(\small{ \ 2\sin\left(x+y\right)\cos\left(x-y\right)=2\sin\left(x+y\right) \ }\)
\(\small{ \ \sin\left(x+y\right)\left\{1-\cos\left(x-y\right)\right\}\leqq 0 \ }\)
\(\small{ \ 1-\cos\left(x-y\right)\geqq 0 \ }\)より
\(\small{ \ \sin\left(x+y\right)\leqq 0 \ }\)または\(\small{ \ 1-\cos\left(x-y\right)=0 \ }\)
ここで\(\small{ \ 0\leqq x \leqq 2\pi \ }\),\(\small{ \ 0\leqq y \leqq 2\pi \ }\)より
\(\small{ \ 0\leqq x+y \leqq 2\pi \ }\)、\(\small{ \ -\pi \leqq x-y \leqq pi \ }\)
\(\small{ \ \sin\left(x+y\right)\leqq 0 \ }\)
\(\small{ \ \pi \leqq x+y \leqq 2\pi \ }\)
\(\small{ \ \therefore -x+\pi \leqq y \leqq -x+2\pi \ }\)
\(\small{ \ 1-\cos\left(x-y\right)=0 \ }\)より
\(\small{ \ \cos\left(x-y\right)=1 \ }\)
\(\small{ \ x-y=0 \ }\)\(\small{ \ \therefore y=x \ }\)
よって図のようになる
ただし、境界線は含む

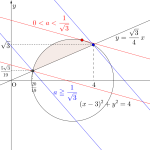
\(\small{ \ y-(x-a)^2=k \ }\)とおくと
\(\small{ \ y=(x-a)^2+k \ }\)
この放物線が求めた領域内を通過すればよい
(i)\(\small{ \ a\lt 0 \ }\)のとき
\(\small{ \ k \ }\)が最大になるのは\(\small{ \ y=(x-a)^2+k \ }\)が\(\small{ \ \left(x, \ y\right)=\left(0, \ \pi\right) \ }\)を通過するとき
よって最大値は\(\small{ \ \pi-a^2 \ }\)
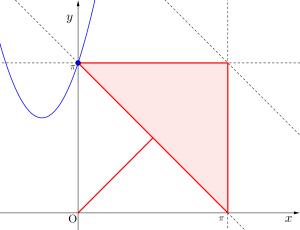
(ii)\(\small{ \ 0 \leqq a \leqq \pi \ }\)のとき
\(\small{ \ k \ }\)が最大になるのは\(\small{ \ y=(x-a)^2+k \ }\)が\(\small{ \ y=\pi \ }\)と接するとき
よって最大値は\(\small{ \ \pi \ }\)

(iii)\(\small{ \ a\gt \pi \ }\)のとき
\(\small{ \ k \ }\)が最大になるのは\(\small{ \ y=(x-a)^2+k \ }\)が\(\small{ \ \left(x, \ y\right)=\left(\pi, \ \pi\right) \ }\)を通過するとき
よって最大値は\(\small{ \ \pi-(\pi-a)^2 \ }\)
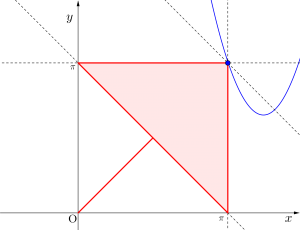
(i)~(iii)より
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
\pi-a^2&\left(a\lt 0\right) \\
\pi&\left(0 \leqq a \leqq \pi\right)\\
\pi-(\pi-a)^2&\left(a\gt \pi\right)
\end{array}
\right.
\end{eqnarray} \ }\)

-

不等式と領域と最大最小(1)
与えられた式の最大最小を満たす点が領域内のどこにあるか見つける方法を詳しく解説しています。
続きを見る
-

不等式と領域と最大最小(2)
式の形によってどの点が最大最小を満たすか詳しく解説しています。
続きを見る