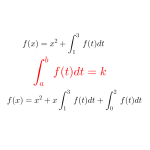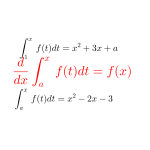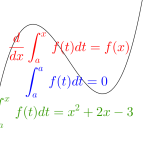定積分で表された関数まとめ

こんにちは、リンス(@Lins016)です。
今回は定積分で表された関数まとめについて学習していきましょう。

定積分で表された関数の違い

「定積分で表された関数」っていうと大きく分けて四つあるんだ。

①積分区間が定数の定積分で表された関数の決定
②積分区間に変数\(\small{ \ x \ }\)を含む定積分で表された関数の決定
③積分区間が定数で二つの文字（変数）を含む関数の決定または最大最小
④積分区間に変数\(\small{ \ x \ }\)を含んだ定積分で表された関数の極大・極小

この四つの問題は見た目は似てるけど解き方は全然違うから、きちんと理解しないといけないからね。

今回はこの四つがどんな問題なのか見ていくことにしよう。

積分区間が定数の定積分で表された関数の決定

この問題の特徴は求める関数の中に積分区間が定数の定積分が含まれていることなんだ。
つまり\(\small{ \ \displaystyle \int_{1}^{3} f(t) dt \ }\)のような定積分が含まれているってこと。
\(\small{ \ \displaystyle \int_{1}^{x} f(t) dt \ }\)とは全く異なるから注意しよう。

\(\small{ \ \displaystyle \int_{1}^{3} f(t) dt \ }\)は\(\small{ \ f(t) \ }\)が定まっていれば定数になるはずだから\(\small{ \ \displaystyle \int_{1}^{3} f(t) dt=k \ }\)として\(\small{ \ k \ }\)を求めよう。

積分区間に変数を含む定積分で表された関数の決定

この問題は\(\small{ \ \displaystyle \int_{1}^{3} f(t) dt \ }\)とは異なり積分区間に\(\small{ \ x \ }\)を含む問題で\(\small{ \ \displaystyle \int_{1}^{x} f(t) dt \ }\)のような問題になる。

この問題は「\(\small{ \ \displaystyle\frac{d}{dx}\displaystyle \int_{a}^{x} f(t) dt=f(x) \ }\)になること」と「\(\small{ \ x=a \ }\)を代入すると\(\small{ \ \displaystyle \int_{a}^{a} f(t) dt=0 \ }\)になること」を利用して問題を解こう。

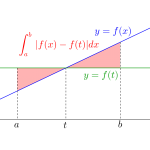
文字を二つ含む定積分で表された関数

この問題は\(\small{ \ \displaystyle \int_{1}^{3} (x^2+xt+t^2) dt \ }\)のように二つの文字が積分含まれている関数で、まずはこの積分を計算して関数を求めることが重要なんだ。

注意するべきところは\(\small{ \ \displaystyle \int_{1}^{3} (x^2+xt+t^2) dt \ }\)の終わりにある\(\small{ \ dt \ }\)の部分で、これが\(\small{ \ dt \ }\)なら\(\small{ \ t \ }\)で積分するし、\(\small{ \ dx \ }\)なら\(\small{ \ x \ }\)で積分しないといけないんだ。

もちろん\(\small{ \ dt \ }\)って書いてあれば\(\small{ \ t \ }\)で積分して、その\(\small{ \ t \ }\)に積分区間を代入するから、\(\small{ \ t \ }\)は消えて\(\small{ \ x \ }\)の関数になるんだ。

積分区間に変数を含む定積分で表された関数の最大最小

この問題は「積分区間に変数を含む定積分で表された関数の決定」をさらに難しくした問題で、極値をとる\(\small{ \ x\ }\)を求めるだけじゃなくて、極値まで求める必要があるんだ。

極値を求めるために計算量が増えるけど、そこまで難しくないから計算ミスをしないように丁寧に計算していこう。

また積分区間の上端と下端に変数\(\small{ \ x \ }\)を含む問題もあるから、定積分を微分する場合は気を付けよう。

どれも見た目は同じような問題に見えるけど解き方は全然違うから、確実に解き方をマスターしておこう。

Point　定積分で表された関数まとめ

①どの形の問題なのか違いを覚える
②各パターンの解き方を覚える