こんにちは、リンス(@Lins016)です。
今回は定積分と面積(基本)について学習していこう。
定積分と面積
放物線や三次関数などの曲線で囲まれた面積は定積分を利用して求めよう。
その前に定積分についてきちんと押さえていない人はまずは定積分を確認しよう。
面積の求め方
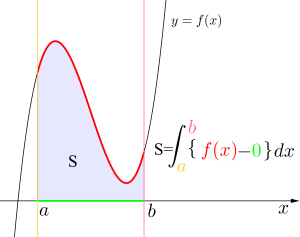
\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx \ }\)は\(\small{ \ y=f(x) \ }\)と直線\(\small{ \ x=a \ }\)、\(\small{ \ x=b \ }\)と\(\small{ \ x \ }\)軸で囲まれた面積になるんだけど、これはあくまで\(\small{ \ y=f(x) \ }\)が\(\small{ \ a\leqq x \leqq b \ }\)で\(\small{ \ y\geqq 0 \ }\)にある場合ね。
もし\(\small{ \ a\leqq x \leqq b \ }\)で\(\small{ \ y\leqq 0 \ }\)なら面積は\(\small{ \ -\displaystyle \int_{a}^{b} f(x) dx \ }\)になるからね。
面積は上の線の関数から下の線の関数を引いた関数を積分しないといけない。
だから、\(\small{ \ a\leqq x \leqq b \ }\)で\(\small{ \ y\geqq 0 \ }\)の場合\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx \ }\)は、本当は\(\small{ \ \displaystyle \int_{a}^{b} \left\{f(x)-0\right\} dx \ }\)になってて\(\small{ \ y=f(x) \ }\)と\(\small{ \ y=0 \ }\)(\(\small{ \ x \ }\)軸)の差を積分してるんだ。
ただ\(\small{ \ 0 \ }\)は書かないから\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx \ }\)が\(\small{ \ y=f(x) \ }\)と直線\(\small{ \ x=a \ }\)、\(\small{ \ x=b \ }\)と\(\small{ \ x \ }\)軸で囲まれた面積ってことになるんだ。

だから\(\small{ \ a\leqq x \leqq b \ }\)で\(\small{ \ y\leqq 0 \ }\)なら\(\small{ \ \displaystyle \int_{a}^{b} \left\{0-f(x)\right\} dx \ }\)ってなるから\(\small{ \ \displaystyle \int_{a}^{b} -f(x) dx \ }\)が求める面積になるからね。
このとき\(\small{ \ \displaystyle \int_{a}^{b} f(x) dx \ }\)を計算すると値はマイナスになるからね。
よく「マイナスになったらマイナスを消してプラスに変えたらいいや」って思ってる人がいるけど、それじゃ今良くてもテストで点数が取れるようにはならないから、必ず関数が\(\small{ \ x \ }\)軸より上にあるか、下にあるか考えよう。
それがテストでも重要なポイントになるからね。
次の曲線と\(\small{ \ 2 \ }\)直線と\(\small{ \ x \ }\)軸で囲まれた面積を求めよ。
(1)\(\small{ \ y=x^2+x, \ x=1, \ x=3 \ }\)
(2)\(\small{ \ y=x^3+x, \ x=1, \ x=3 \ }\)
(1)
\(\small{\begin{eqnarray} \ S&=&\displaystyle \int_{1}^{3} (x^2+x) dx\\
&=&\left[\displaystyle\frac{1}{3}x^3+\displaystyle\frac{1}{2}x^2\right]_{1}^{3}\\
&=&\displaystyle\frac{38}{3} \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ S&=&\displaystyle \int_{1}^{3} (x^3+x) dx\\
&=&\left[\displaystyle\frac{1}{4}x^4+\displaystyle\frac{1}{2}x^2\right]_{1}^{3}\\
&=&24 \ \end{eqnarray}}\)

二つの関数で囲まれる面積
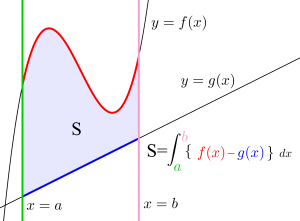
今度は\(\small{ \ y=f(x) \ }\)と\(\small{ \ y=g(x) \ }\)と\(\small{ \ x=a \ }\)、\(\small{ \ x=b \ }\)で囲まれた面積について考えていこう。
ここでも\(\small{ \ y=f(x) \ }\)と\(\small{ \ y=g(x) \ }\)のどっちの関数が\(\small{ \ a\leqq x \leqq b \ }\)のとき上にあるかってことが重要になるんだ。
\(\small{ \ y=f(x) \ }\)が上にある場合、図のように\(\small{ \ y=f(x) \ }\)と\(\small{ \ x \ }\)軸と\(\small{ \ x=a \ }\)、\(\small{ \ x=b \ }\)で囲まれた面積\(\small{ \ S_1 \ }\)(赤い斜線部)から\(\small{ \ y=g(x) \ }\)と\(\small{ \ x \ }\)軸と\(\small{ \ x=a \ }\)、\(\small{ \ x=b \ }\)で囲まれた面積\(\small{ \ S_2 \ }\)(青い斜線部)を引いた部分の面積(緑)が求める面積になるよね。
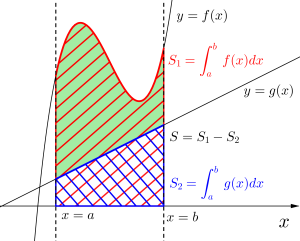
\(\small{\begin{eqnarray} \ S&=&S_1-S_2\\
&=&\displaystyle \int_{a }^{b} f(x) dx-\displaystyle \int_{a}^{b} g(x) dx\\
&=&\displaystyle \int_{a }^{b}\left\{ f(x)-g(x)\right\} dx \ \end{eqnarray}}\)

このことから\(\small{ \ y=f(x) \ }\)の方が上にあるなら、求める面積は\(\small{ \ \displaystyle \int_{a}^{b} \left\{f(x)-g(x)\right\} dx \ }\)になるし、\(\small{ \ y=g(x) \ }\)の方が上にあるなら、求める面積は\(\small{ \ \displaystyle \int_{a}^{b} \left\{g(x)-f(x)\right\} dx \ }\)なるんだ。
だからどっちの関数が\(\small{ \ a\leqq x \leqq b \ }\)の範囲で上側にあるか考える必要があるからね。
\(\small{ \ y=x^2-5x \ }\)と\(\small{ \ y=-x^2+4x \ }\)と\(\small{ \ x=1 \ }\)、\(\small{ \ x=2 \ }\)で囲まれた面積を求めよ。
求める面積は
\(\small{ \ \displaystyle \int_{1 }^{2 } \left\{(-x^2+4x)-(x^2-5x)\right\}dx\\
=\displaystyle \int_{1 }^{2}(-2x^2+9x) dx\\
=\left[-\displaystyle\frac{2}{3}x^3+\displaystyle\frac{9}{2}x^2\right]_{1}^{2}\\
=\displaystyle\frac{55}{6} \ }\)


どっちの関数が上にあるか下にあるかだけ調べればいいから、その積分区間内にある簡単な数値を代入して調べてもいいからね。
Point 定積分の計算と面積
①面積は上の線引く下の線を積分する

