こんにちは、リンス(@Lins016)です。
今回は【文系必須】放物線と接線と面積について学習していこう。
放物線と接線と面積
今回は放物線\(\small{ \ C: y=kx^2 \ }\)上の二点\(\small{ \ \mathrm{A}(a, \ ka^2) \ }\)、\(\small{ \ \mathrm{B}(b, \ kb^2) \ }\)から展開される一連の流れについて考えていこう。ちなみに\(\small{ \ a, \ b \ }\)は\(\small{ \ a\lt b \ }\)を満たす実数ね。
理系だと国公立二次試験や私立大の微分積分の問題は数学Ⅲの微分積分から出題されることがほとんどだけど、文系だと数学Ⅲは範囲外だから数学Ⅱの微分積分から出題されるよね。しかも微分積分を出題する学校は本当に多いからね。
今回は数学Ⅱの微分積分の中でも最も出題される放物線の問題を考えていくから、文系の人は確実に押さえておこう。
もちろん理系の人もね。
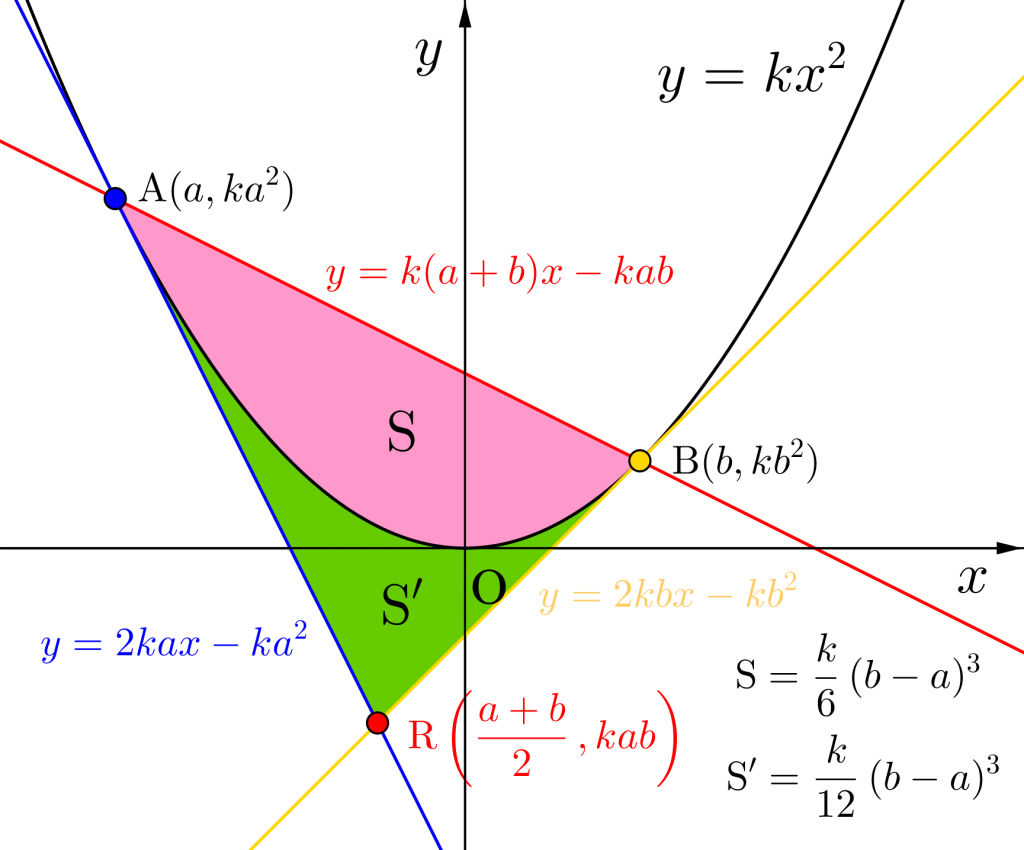
放物線上の二点を通る直線
放物線\(\small{ \ C: y=kx^2 \ }\)上の二点\(\small{ \ \mathrm{A}(a, \ ka^2) \ }\)、\(\small{ \ \mathrm{B}(b, \ kb^2) \ }\)を通る直線\(\small{ \ \mathrm{AB} \ }\)の方程式を\(\small{ \ a \ }\)と\(\small{ \ b \ }\)を用いて表してみよう。
直線\(\small{ \ \mathrm{AB} \ }\)の方程式は\(\small{ \ \mathrm{A}(a, \ ka^2) \ }\)、\(\small{ \ \mathrm{B}(b, \ kb^2) \ }\)を通るから
\(\small{\begin{eqnarray} \ y&=&\displaystyle\frac{kb^2-ka^2}{b-a}(x-a)+a^2\\
&=&k(a+b)x-kab \ \end{eqnarray}}\)
\(\small{ \ \therefore \ y=k(a+b)x-kab \ }\)
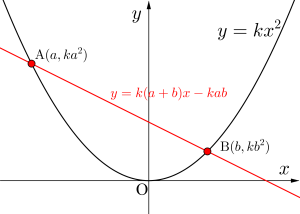
放物線と直線で囲まれる面積
次に放物線\(\small{ \ C \ }\)とこの直線\(\small{ \ \mathrm{AB} \ }\)で囲まれた面積\(\small{ \ \mathrm{S} \ }\)を\(\small{ \ a \ }\)と\(\small{ \ b \ }\)を用いて表してみよう。
求める面積\(\small{ \ \mathrm{S} \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\int_{a}^{b}\left\{k(a+b)x-kab-kx^2\right\}dx\\
&=&-k\displaystyle\int_{a}^{b}(x-a)(x-b)dx\\
&=&\displaystyle\frac{k}{6}(b-a)^3 \ \end{eqnarray}}\)
\(\small{ \ \therefore \ \mathrm{S}=\displaystyle\frac{k}{6}(b-a)^3 \ }\)

この面積は放物線と直線の二本で囲まれた面積になるから\(\small{ \ \displaystyle\frac{1}{6} \ }\)公式が使えるからね。
放物線上の点における接線の方程式
次に二点\(\small{ \ \mathrm{A}(a, \ ka^2) \ }\)、\(\small{ \ \mathrm{B}(b, \ kb^2) \ }\)における接線の方程式を求めてみよう。
\(\small{ \ y=kx^2 \ }\)を微分すると\(\small{ \ y'=2kx \ }\)になるから
\(\small{ \ \mathrm{A}(a, \ ka^2) \ }\)における接線の方程式は
\(\small{\begin{eqnarray} \ y&=&2ka(x-a)+ka^2\\
&=&2kax-ka^2 \ \end{eqnarray}}\)
同様に\(\small{ \ \mathrm{B}(b, \ kb^2) \ }\)における接線の方程式は
\(\small{\begin{eqnarray} \ y&=&2kb(x-b)+kb^2\\
&=&2kbx-kb^2 \ \end{eqnarray}}\)
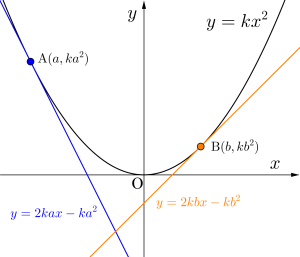
二接線の交点の座標
二点\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)における接線の共有点\(\small{ \ \mathrm{R} \ }\)は
\(\small{ \ 2kax-ka^2=2kbx-kb^2 \ }\)
\(\small{ \ 2k(a-b)x=k(a^2-b^2) \ }\)
\(\small{ \ a\neq b \ }\)より
\(\small{ \ x=\displaystyle\frac{a+b}{2} \ }\)
よって二接線の共有点\(\small{ \ \mathrm{R} \ }\)の座標はこれを接線に代入して
\(\small{ \ \mathrm{R}\left(\displaystyle\frac{a+b}{2}, \ kab\right) \ }\)

放物線と二接線で囲まれる面積
二つの接線と放物線\(\small{ \ C \ }\)で囲まれた面積\(\small{ \ \mathrm{S’} \ }\)について考えてみよう。
積分区間に注意して
&=&\displaystyle\int_{a}^{\tiny{\displaystyle\frac{a+b}{2}}}\left\{kx^2-(2kax-ka^2)\right\}dx+\displaystyle\int_{\tiny{\displaystyle\frac{a+b}{2}}}^{b}\left\{kx^2-(2kbx-kb^2)\right\}dx\\
&=&\displaystyle\int_{a}^{\tiny{\displaystyle\frac{a+b}{2}}}(kx^2-2kax+ka^2)dx+\displaystyle\int_{\tiny{\displaystyle\frac{a+b}{2}}}^{b}(kx^2-2kbx+kb^2)dx\\
&=&\displaystyle\int_{a}^{\tiny{\displaystyle\frac{a+b}{2}}}k(x-a)^2dx+\displaystyle\int_{\tiny{\displaystyle\frac{a+b}{2}}}^{b}k(x-b)^2dx\\
&=&\left[\displaystyle\frac{k}{3}(x-a)^3\right]_{a}^{\tiny{\displaystyle\frac{a+b}{2}}}+\left[\displaystyle\frac{k}{3}(x-b)^3\right]_{\tiny{\displaystyle\frac{a+b}{2}}}^{b}\\
&=&\displaystyle\frac{k}{3}\left(\displaystyle\frac{b-a}{2}\right)^3-\displaystyle\frac{k}{3}\left(\displaystyle\frac{a-b}{2}\right)^3\\
&=&\displaystyle\frac{k}{12}(b-a)^3 \ \end{eqnarray}}\)
\(\small{ \ \therefore \ \mathrm{S'}=\displaystyle\frac{k}{12}(b-a)^3 \ }\)
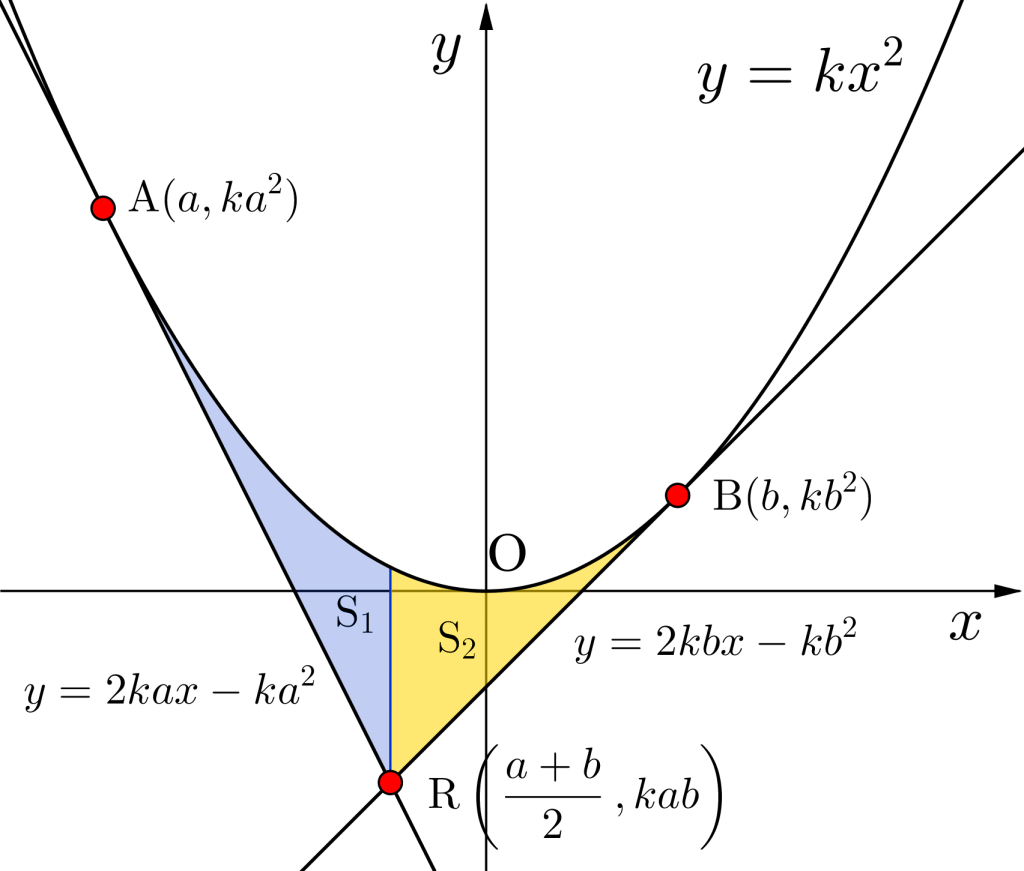
\(\small{ \ \mathrm{S}=\displaystyle\frac{k}{6}(b-a)^3 \ }\)
\(\small{ \ \mathrm{S'}=\displaystyle\frac{k}{12}(b-a)^3 \ }\)だから
\(\small{ \ \mathrm{S}:\mathrm{S'}=2:1 \ }\)が言えるよね。
つまり二点の座標にかかわらず面積比は一定になるってことがいえるんだ。
Point 放物線と接線と面積
①放物線上の二点の各接線や二点を通る直線を求める
②放物線上の二点を通る直線と放物線で囲まれた面積とその二点の接線と放物線で囲まれた面積の比は二点の座標によらない
放物線\(\small{ \ C:y=x^2+2 \ }\)上に異なる\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{A}(a, \ a^2+2) \ }\)と点\(\small{ \ \mathrm{B}(b, \ b^2+2) \ }\)(\(\small{ \ a\lt b \ }\))をとる。点\(\small{ \ \mathrm{A} \ }\)における\(\small{ \ C \ }\)の接線と点\(\small{ \ \mathrm{B} \ }\)における\(\small{ \ C \ }\)の接線との交点を\(\small{ \ \mathrm{P} \ }\)とし、\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{A}, \ \mathrm{B} \ }\)を通る直線と放物線\(\small{ \ C \ }\)で囲まれた図形の面積を\(\small{ \ \mathrm{S} \ }\)とする。
(1)点\(\small{ \ \mathrm{P} \ }\)の座標を求めよ。
(2)\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{A}, \ \mathrm{B} \ }\)が\(\small{ \ \mathrm{S} \ }\)が\(\small{ \ \displaystyle\frac{1}{6} \ }\)を保って動くとき、点\(\small{ \ \mathrm{P} \ }\)はどのような方程式で表される曲線上を動くか。
(3)点\(\small{ \ \mathrm{P} \ }\)が原点を中心とする半径\(\small{ \ 1 \ }\)の円周上を動くとき、\(\small{ \ \mathrm{S} \ }\)を最大、最小にする点\(\small{ \ \mathrm{P} \ }\)の座標を求めよ。
(1)\(\small{ \ y=x^2+2 \ }\)を微分すると
\(\small{ \ y`=2x \ }\)より
点\(\small{ \ \mathrm{A}(a, \ a^2+2) \ }\)における接線の方程式は
\(\small{\begin{eqnarray} \ y&=&2a(x-a)+a^2+2\\
&=&2ax-a^2+2 \ \end{eqnarray}}\)
点\(\small{ \ \mathrm{B}(b, \ b^2+2) \ }\)における接線の方程式は
\(\small{\begin{eqnarray} \ y&=&2b(x-b)+b^2+2\\
&=&2bx-b^2+2 \ \end{eqnarray}}\)
点\(\small{ \ \mathrm{P} \ }\)の\(\small{ \ x \ }\)座標は
\(\small{ \ 2ax-a^2+2=2bx-b^2+2 \ }\)
\(\small{ \ 2(a-b)x=a^2-b^2 \ }\)
\(\small{ \ a \lt b \ }\)より\(\small{ \ x=\displaystyle\frac{a+b}{2} \ }\)
よって点\(\small{ \ \mathrm{P} \ }\)の\(\small{ \ y \ }\)座標は
\(\small{\begin{eqnarray} \ y&=&2a\cdot\displaystyle\frac{a+b}{2}-a^2+2\\
&=&ab+2 \ \end{eqnarray}}\)
\(\small{ \ \therefore \ \mathrm{P}\left(\displaystyle\frac{a+b}{2}, \ ab+2\right) \ }\)
(2)\(\small{ \ 2 \ }\)点\(\small{ \ \mathrm{A}, \ \mathrm{B} \ }\)を通る直線の方程式は
\(\small{\begin{eqnarray} \ y&=&\displaystyle\frac{(b^2+2)-(a^2+2)}{b-a}(x-a)+a^2+2\\
&=&(a+b)x-ab+2 \ \end{eqnarray}}\)
この直線と放物線\(\small{ \ C \ }\)との交点の\(\small{ \ x \ }\)座標は\(\small{ \ x=a, \ b \ }\)だから
\(\small{ \begin{eqnarray}\ \mathrm{S}&=&\displaystyle \int_{a}^{b} \left[\left\{(a+b)x-ab+2\right\}-(x^2+2)\right] dx\\
&=&\displaystyle \int_{a}^{b} -(x-a)(x-b) dx\\
&=&\displaystyle\frac{1}{6}(b-a)^3 \ \end{eqnarray}}\)
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{6} \ }\)より\(\small{ \ b-a=1 \ }\)
\(\small{\begin{eqnarray} \ \mathrm{P}\left(x, \ y\right)&=&\left(\displaystyle\frac{a+b}{2}, \ ab+2\right)\\
&=&\left(\displaystyle\frac{2a+1}{2},a^2+a+2\right) \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
x=\displaystyle\frac{2a+1}{2}\cdots①\\
y=a^2+a+2\cdots②
\end{array}
\right.
\end{eqnarray} \ }\)
\(\small{①}\)より\(\small{ \ a=\displaystyle\frac{2x-1}{2} \ }\)
これを\(\small{②}\)に代入すると
\(\small{\begin{eqnarray} \ y&=&\left(\displaystyle\frac{2x-1}{2}\right)^2+\displaystyle\frac{2x-1}{2}+2\\
&=&x^2+\displaystyle\frac{7}{4} \ \end{eqnarray}}\)
よって求める方程式は\(\small{ \ y=x^2+\displaystyle\frac{7}{4} \ }\)
(3)\(\small{ \ \mathrm{P}(x, \ y)=\left(\displaystyle\frac{a+b}{2},ab+2\right) \ }\)とすると、
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
a+b=2x\\
ab=y-2
\end{array}
\right.
\end{eqnarray} \ }\)
またこの点は原点を中心とする半径\(\small{ \ 1 \ }\)の円周上を動くから
\(\small{ \ x^2+y^2=1 \ }\)
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{6}(b-a)^3 \ }\)より
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{6}(b-a)^3\\
&=&\displaystyle\frac{1}{6}\left\{(b-a)^2\right\}^{\tiny{\displaystyle\frac{3}{2}}}\\
&=&\displaystyle\frac{1}{6}\left\{(b+a)^2-4ab\right\}^{\tiny{\displaystyle\frac{3}{2}}}\\
&=&\displaystyle\frac{1}{6}\left\{(2x)^2-4(y-2)\right\}^{\tiny{\displaystyle\frac{3}{2}}}\\
&=&\displaystyle\frac{1}{6}(4x^2-4y+8)^{\tiny{\displaystyle\frac{3}{2}}}\\
&=&\displaystyle\frac{1}{6}\left\{4(1-y^2)-4y+8\right\}^{\tiny{\displaystyle\frac{3}{2}}}\\
&=&\displaystyle\frac{1}{6}\left\{-4\left(y+\displaystyle\frac{1}{2}\right)^2+13\right\}^{\tiny{\displaystyle\frac{3}{2}}} \ \end{eqnarray}}\)
\(\small{ \ -1\leqq y \leqq 1 \ }\)より
\(\small{ \ y=-\displaystyle\frac{1}{2} \ }\)のとき\(\small{ \ \mathrm{S} \ }\)は最大
\(\small{ \ y=1 \ }\)のとき\(\small{ \ \mathrm{S} \ }\)は最小
\(\small{ \ y=-\displaystyle\frac{1}{2} \ }\)のとき\(\small{ \ x=\pm\displaystyle\frac{\sqrt{3}}{2} \ }\)
\(\small{ \ y=1 \ }\)のとき\(\small{ \ x=0 \ }\)
よって
\(\small{ \ \mathrm{P}\left(\pm\displaystyle\frac{\sqrt{3}}{2}, \ -\displaystyle\frac{1}{2}\right) \ }\)のとき最大
\(\small{ \ \mathrm{P}\left(0, \ 1\right) \ }\)のとき最小

今回の問題は点Pの軌跡を利用する問題だったから、軌跡の方程式を忘れてる人はもう一度確認しておこう。

