こんにちは、リンス(@Lins016)です。
今回は二次方程式の解の存在範囲(解の配置)について学習していこう。
解の存在範囲(解の配置)
二次方程式の解の存在範囲は解と係数の関係を利用する方法もあるけど、今回はグラフを利用して解の存在範囲を確認していこう。
\(\small{ \ f(x)=ax^2+bx+c=0 \ }\)(\(\small{ \ a\gt0 \ }\)のとき)
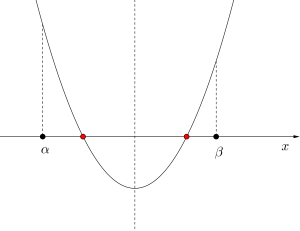
・\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ \alpha \lt x \lt \beta \ }\)にある。
\(\small{ \ D=b^2-4ac \geqq 0 \ }\)
\(\small{ \ \alpha \lt 軸 \left(-\displaystyle \frac{b}{2a} \right) \lt \beta \ }\)
\(\small{ \ f(\alpha)\gt0 \ }\)
\(\small{ \ f(\beta)\gt0 \ }\)
※異なる\(\small{ \ 2 \ }\)つの解の場合は判別式\(\small{ \ D \gt 0 \ }\)
・\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ \alpha \ }\)より大きい
\(\small{ \ D=b^2-4ac \geqq 0 \ }\)
\(\small{ \ 軸\left(-\displaystyle \frac{b}{2a}\right) \gt \alpha \ }\)
\(\small{ \ f(\alpha)\gt0 \ }\)
※異なる\(\small{ \ 2 \ }\)つの解の場合\(\small{ \ D \gt 0 \ }\)

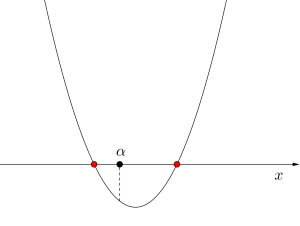
・\(\small{ \ 2 \ }\)つの解のうち\(\small{ \ 1 \ }\)つは\(\small{ \ \alpha \ }\)より小さくて、もう\(\small{ \ 1 \ }\)つは\(\small{ \ \alpha \ }\)より大きい
\(\small{ \ f(\alpha)\lt 0 \ }\)
グラフから解の存在範囲を考えよう
解の存在範囲はグラフを書いて考えるのが一番わかりやすいかな。
例えば異なる\(\small{ \ 2 \ }\)つの解が\(\small{ \ \alpha \ }\)と\(\small{ \ \beta \ }\)の間にある場合について考えてみよう。
まず解が\(\small{ \ 2 \ }\)つあるから判別式が正っていえるよね。
でもこれだと図の青いグラフにもなるから条件を満たすとは言えないよね。
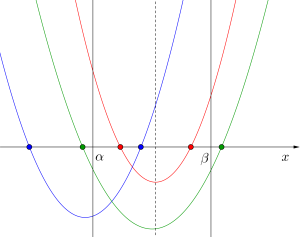
条件を満たすには軸が\(\small{ \ \alpha \ }\)と\(\small{ \ \beta \ }\)の間にないといけないよね。でもそれだけじゃ緑のグラフにもなりえるからまだ条件が足りない。
緑と赤のグラフの違いは\(\small{ \ f(\alpha) \ }\)と\(\small{ \ f(\beta) \ }\)の値が正か負かの違いだから、そこまで考える事で条件を満たすグラフを考える事ができるんだ。
\(\small{ \ \alpha \lt x \lt \beta \ }\)に2つの解をもつ場合
\(\small{ \ ax^2+bx+c=0 \ }\)の\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ \alpha \lt x \lt \beta \ }\)にあるなら、「判別式」「軸の位置」「区間の端をグラフが通る位置」について考えないといけない。
\(\small{ \ f(x)=ax^2+bx+c=0 \ }\)(\(\small{ \ a\gt0 \ }\)のとき)
①判別式
\(\small{ \ D=b^2-4ac \geqq 0 \ }\)
②軸の位置
\(\small{ \ \alpha \lt -\displaystyle \frac{b}{2a} \lt \beta \ }\)
③区間の端をグラフが通る位置
\(\small{ \ f(\alpha)\gt0 \ }\)
\(\small{ \ f(\beta)\gt0 \ }\)

この条件を満たせばグラフは図のようになるから、\(\small{ \ ax^2+bx+c=0 \ }\)の\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ \alpha \lt x \lt \beta \ }\)にあるって言えるんだ。
ちなみに\(\small{ \ 2 \ }\)つの解は重解も含むから\(\small{ \ D\geqq0 \ }\)になるけど、異なる\(\small{ \ 2 \ }\)つの解なら\(\small{ \ D\gt0 \ }\)になるからね。
また、\(\small{ \ \alpha \leqq x \leqq \beta \ }\)なら\(\small{ \ f(\alpha)\geqq0 \ , \ f(\beta)\geqq0 \ }\)になるから注意しよう。
\(\small{ \ x \gt \alpha \ }\)に2つの解をもつ場合
\(\small{ \ ax^2+bx+c=0 \ }\)の\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ x \gt \alpha \ }\)にあるなら、「判別式」「軸の位置」「区間の端をグラフが通る位置」について考えないといけない。これは上の「\(\small{ \ \alpha \lt x \lt \beta \ }\)に\(\small{ \ 2 \ }\)つの解をもつ場合」と同じだからね。
\(\small{ \ f(x)=ax^2+bx+c=0 \ }\)(\(\small{ \ a\gt0 \ }\)のとき)
①判別式
\(\small{ \ D=b^2-4ac \geqq 0 \ }\)
②軸の位置
\(\small{ \ -\displaystyle \frac{b}{2a} \gt \alpha \ }\)
③区間の端をグラフが通る位置
\(\small{ \ f(\alpha)\gt0 \ }\)

この条件を満たせばグラフは図のようになるから、\(\small{ \ ax^2+bx+c=0 \ }\)\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ x \gt\alpha \ }\)にあるって言えるんだ。
この場合も異なる\(\small{ \ 2 \ }\)つの解ってなると\(\small{ \ D\gt0 \ }\)になるからね。
αより大きい解と小さい解をもつ場合
\(\small{ \ 2 \ }\)つの解のうち\(\small{ \ 1 \ }\)つは\(\small{ \ \alpha \ }\)より大きくて、もう\(\small{ \ 1 \ }\)つは\(\small{ \ \alpha \ }\)より小さい場合、\(\small{ \ f(\alpha)\lt 0 \ }\)だけを満たせばいいんだ。つまり判別式すら考えなくていいということ。
これってあくまで下に凸のグラフ、つまり\(\small{ \ x^2 \ }\)の係数が正の場合に限るんだけど、下に凸のグラフが負の部分を通るってことは、いつか増加して正の値になるから解を持つから、判別式すら必要ないんだ。
\(\small{ \ f(\alpha)\lt 0 \ }\)

\(\small{ \ 2 \ }\)次方程式\(\small{ \ x^2+kx+2k-1=0 \ }\)が次の条件を満たすように定数\(\small{ \ k \ }\)の範囲を求めよ。
(1)異なる\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ -1 \ }\)より小さい
(2)異なる\(\small{ \ 2 \ }\)つの解がともに\(\small{ \ -2 \ }\)と\(\small{ \ 5 \ }\)の間にある
\(\small{ \ f(x)=x^2+kx+2k-1 \ }\)とする
(1)異なる\(\small{ \ 2 \ }\)つの解を持つので
\(\small{ \ D=k^2-8k+4\gt0 \ }\)
\(\small{ \ k^2-8k+4=0 \ }\)とすると
\(\small{ \ k=4\pm2\sqrt{3} \ }\)
よって\(\small{ \ k \lt 4-2\sqrt{3}, \ k \gt 4+2\sqrt{3} \cdot① }\)
軸が\(\small{ \ -2 \ }\)より小さいので
\(\small{ \ -\displaystyle \frac{k}{2}\lt-1 \ }\)
\(\small{ \ \therefore k \gt 2 \ }\)
\(\small{ \ f(-1)\gt0 \ }\)であればよいので
\(\small{ \ f(-1)=k\gt0\cdots③ \ }\)
\(\small{ \ ①②③ \ }\)より
\(\small{ \ k\gt4+2\sqrt{3} \ }\)
(2)異なる\(\small{ \ 2 \ }\)つの解を持つので\(\small{ \ D\gt0 \ }\)より
\(\small{ \ k \lt 4-2\sqrt{3}, \ k \gt 4+2\sqrt{3} \cdot① }\)
軸が\(\small{ \ -2 \ }\)と\(\small{ \ 5 \ }\)の間にあり、
\(\small{ \ f(-2) \ }\)と\(\small{ \ f(5) \ }\)が正であればよい
\(\small{ \ -2\lt -\displaystyle \frac{k}{2}\lt5 \ }\)
\(\small{ \ \therefore -10 \lt k\lt 4 \cdots② }\)
\(\small{ \ f(-2)=3\gt0 \ }\)
\(\small{ \ f(5)=7k+24\gt0 \ }\)\(\small{ \ \therefore k\gt-\displaystyle \frac{24}{7} \cdots③ }\)
\(\small{ \ ①②③ \ }\)より
\(\small{ \ -\displaystyle \frac{24}{7} \lt k \lt4-2\sqrt{3} \ }\)

Point 二次方程式の解の存在範囲(解の配置)
①存在範囲を満たす条件をきちんと考えよう
②軸や定義域の端の\(\small{ \ y \ }\)座標に注意しよう
方程式\(\small{ \ x^4-ax^2+a^2-a-2=0 \ }\)が相異なる\(\small{ \ 4 \ }\)つの実数解を持つとき、実数\(\small{ \ a \ }\)のとりうる値の範囲を求めよ。
\(\small{ \ x^2=t \ }\)とすると
\(\small{ \ t^2-at+a^2-a-2=0 \ }\)と\(\small{ \ t \ }\)の二次方程式になるので
この二次方程式の解が正の異なる\(\small{ \ 2 \ }\)つの解を持てばよい。
\(\small{ \ f(t)=t^2-at+a^2-a-2 \ }\)とすると
異なる解を\(\small{ \ 2 \ }\)つ持つので
\(\small{ \ D\gt0 \ }\)
\(\small{ \ (-a)^2-4(a^2-a-2)\gt0 \ }\)
\(\small{ \ 3a^2-4a-8\lt 0 \ }\)
\(\small{ \ 3a^2-4a-8=0 \ }\)とおくと
\(\small{ \ a=\displaystyle \frac{2\pm2\sqrt{7}}{3} \ }\)
よって\(\small{ \ \displaystyle \frac{2-2\sqrt{7}}{3}\lt a \lt \displaystyle \frac{2+2\sqrt{7}}{3}\cdots① \ }\)
正の解を\(\small{ \ 2 \ }\)つ持つので
軸が正かつ\(\small{ \ f(0)\gt0 \ }\)であればよい
\(\small{ \ \displaystyle \frac{a}{2}\gt 0 \ }\)\(\small{ \ \therefore a\gt 0 \cdots② \ }\)
\(\small{\begin{eqnarray} \ f(0)&=&a^2-a-2\\
&=&(a+1)(a-2)\gt0 \ \end{eqnarray}}\)
\(\small{ \ \therefore a\lt-1, \ a\gt2 \cdots③ }\)
\(\small{ \ ①, \ ②, \ ③ \ }\)より
\(\small{ \ 2\lt a \lt \displaystyle \frac{2+2\sqrt{7}}{3} \ }\)

