こんにちは、リンス(@Lins016)です。
今回は文字係数を含む3次関数の最大最小について学習していこう。
3次関数の最大最小の場合分け
今回学習するのは\(\small{ \ x \ }\)の係数に\(\small{ \ a \ }\)などの定数が付いていて、定義域が固定されてる関数の最大最小だ。ここで重要なのは、\(\small{ \ x \ }\)の係数に\(\small{ \ a \ }\)が付いているってこと、つまり微分しても\(\small{ \ a \ }\)が残っているってことだ。\(\small{ \ f'(x) \ }\)に\(\small{ \ a \ }\)があるってことは\(\small{ \ f'(x)=0 \ }\)の解にも\(\small{ \ a \ }\)が入ってくるよね。むしろ\(\small{ \ a \ }\)の値によっては解を持たないかもしれない。つまり\(\small{ \ a \ }\)の範囲によっては極値を持つ関数になったり、極値を持たない関数になるから、まずはそこで\(\small{ \ a \ }\)についての場合分けが必要になるよね。
極値を持たない場合
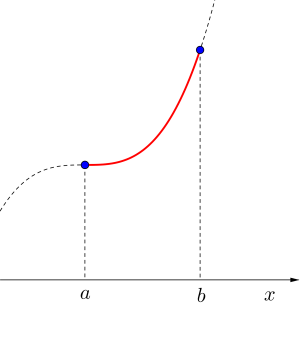
極値が定義域内にある場合(1)
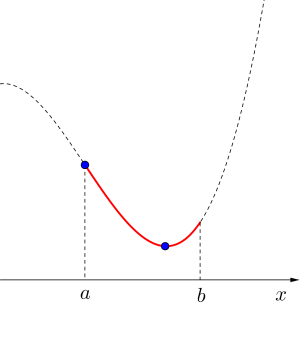
極値が定義域内にある場合(2)
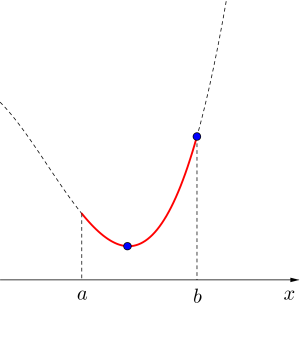
極値が定義域外にある場合
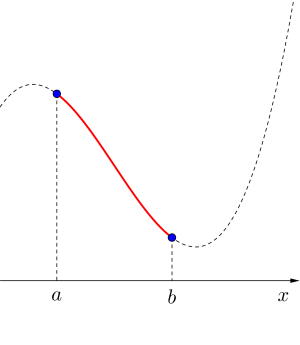
極値を持たない場合の最大最小
極値を持たない3次関数のグラフは単調増加か単調減少のグラフになるから定義域の両端が最大値と最小値になるから単純に求めることができるから問題ないよね。
極値を持つ場合の最大最小
極値を持つ場合は考えないといけないことがいくつかある。まずは極値をとる\(\small{ \ x \ }\)の値が定義域外にあるか、それとも定義域内にあるか。極値をとる\(\small{ \ x \ }\)が定義域外にある場合は定義域ではグラフは単調増加か単調減少になるから定義域の両端が最大値最小値になる。
極値の一方が定義域内にある場合、極値と定義域の両端の値を比較して最大最小を求めよう。極値が極大値の場合は極大値が最大値になって定義域の両端のどちらかが最小値になる。極値が極小値の場合は極小値が最小値になって定義域の両端のどちらかが最大値になる。どちらにしても定義域の両端の大小関係も求める必要があるから、丁寧に問題を解く必要がある。グラフを書いてしっかりと解くようにしよう。
\(\small{ \ a \geqq 0 \ }\)とする. 関数\(\small{ \ f(x)=x^3-a^2x \ }\)について, \(\small{ \ 0\leqq x \leqq 1 \ }\)における最大値と最小値を求めよ.
\(\small{ \ f(x)=x^3-a^2x \ }\)
\(\small{ \ f'(x)=3x^2-a^2=(\sqrt{3}x+a)(\sqrt{3}x-a) \ }\)
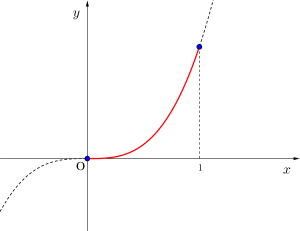
(i)\(\small{ \ a=0 \ }\)のとき
\(\small{ \ f'(x)=3x^2 \ }\)となり, \(\small{ \ f(x) \ }\)は単調増加より
最大値\(\small{ \ 1 \ (x=1) \ }\)
最小値\(\small{ \ 0 \ (x=0) \ }\)
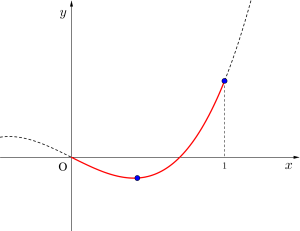
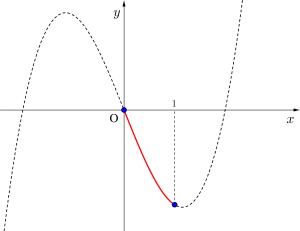
(ii)\(\small{ \ 0 \lt \displaystyle \frac{a}{\sqrt{3}}\leqq 1 \ }\)
\(\small{ \ \therefore 0 \lt a \leqq \sqrt{3} \ }\)のとき
\(\small{ \ \begin{array}{c|ccccc}
x & 0 & \cdots & \displaystyle \frac{a}{\sqrt{3}} & \cdots & 1 \\
\hline
f’(x) & & - & 0 & + & \\
\hline
f(x) & 0 & \searrow & -\displaystyle \frac{2a^3}{3\sqrt{3}} & \nearrow & 1-a^2
\end{array} \ }\)
よって最小値\(\small{ \ -\displaystyle \frac{2a^3}{3\sqrt{3}} \ \left(x=\displaystyle \frac{a}{\sqrt{3}}\right) \ }\)
最大値は\(\small{ \ 0 \ }\)と\(\small{ \ 1-a^2 \ }\)の大小を考えて、
\(\small{ \ 0\lt a \leqq 1 \ }\)のとき最大値\(\small{ \ 1-a^2 \ (x=1) \ }\)
\(\small{ \ 1\lt a \leqq \sqrt{3} \ }\)のとき最大値\(\small{ \ 0 \ (x=0) \ }\)
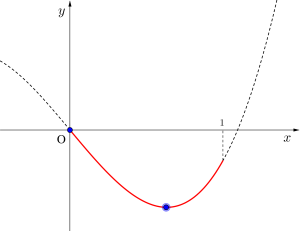
(iii)\(\small{ \ \displaystyle \frac{a}{\sqrt{3}}\gt 1 \ }\)
\(\small{ \ \therefore a \gt \sqrt{3} \ }\)
\(\small{ \ \begin{array}{c|ccccc}
x & 0 & \cdots & 1 \\
\hline
f’(x) & & - & \\
\hline
f(x) & 0 & \searrow & 1-a^2
\end{array} \ }\)
よって最大値\(\small{ \ 0 \ (x=0) \ }\)
最小値\(\small{ \ 1-a^2 \ (x=1) \ }\)

Point
①極値を持つ持たないで定数の範囲を場合分け
②極値と定義域の両端の値を比較
区間\(\small{ \ 0 \leqq x \leqq 1 \ }\)において、関数\(\small{ \ f(x)=-x^3+3ax \ }\)の最大値と最小値を求めよ。ただし\(\small{ \ a \ }\)は定数である。
\(\small{ \ f(x)=-x^3+3ax \ }\)より
\(\small{ \ f'(x)=-3x^2+3a \ }\)
\(\small{ \ f'(x)=0 \ }\)の判別式\(\small{ \ D \ }\)は
\(\small{ \ D=36a \ }\)
\(\small{ \ D\leqq 0 \ }\)のとき\(\small{ \ a\leqq 0 \ }\)
\(\small{ \ D\gt 0 \ }\)の時\(\small{ \ a \gt 0 \ }\)
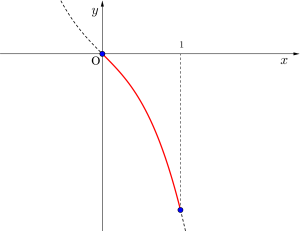
(i)\(\small{ \ a \leqq 0 \ }\)のとき
\(\small{ \ f'(x) \leqq 0 \ }\)より\(\small{ \ f(x) \ }\)は単調減少
よって最大値\(\small{ \ 0 \ (x=0) \ }\)
最小値\(\small{ \ 3a-1 \ (x=1) \ }\)
(ii)\(\small{ \ a \gt 0 \ }\)のとき\(\small{ \ f(x) \ }\)は極値を持つ
\(\small{ \ \begin{array}{c|ccccc}
x & \cdots & -\sqrt{a} & \cdots & \sqrt{a} & \cdots \\
\hline
f’(x) & - & 0 & + & 0 & - \\
\hline
f(x) & \searrow & & \nearrow & & \searrow
\end{array} \ }\)
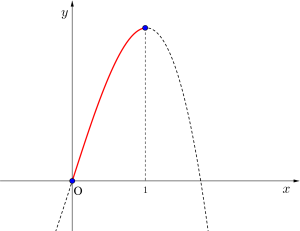
1)\(\small{ \ \sqrt{a} \gt 1 \ }\) \(\small{ \ \therefore a \gt 1 \ }\)のとき
区間\(\small{ \ 0 \leqq x \leqq 1 \ }\)において\(\small{ \ f(x) \ }\)は単調増加
よって最大値\(\small{ \ 3a-1 \ (x=1) \ }\)
最小値\(\small{ \ 0 \ (x=0) \ }\)
2)\(\small{ \ 0 \lt \sqrt{a} \leqq 1 \ }\)\(\small{ \ \therefore 0 \lt a \leqq 1 \ }\)のとき
\(\small{ \ f(0)=0 \ }\)と\(\small{ \ f(1)=3a-1 \ }\)の大小を比較して
\(\small{ \ 0 \lt a \leqq \displaystyle \frac{1}{3} \ }\)のとき
最大値\(\small{ \ 2a\sqrt{a} \ (x=\sqrt{a}) \ }\)
最小値\(\small{ \ 3a-1 \ (x=1) \ }\)
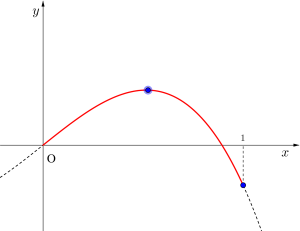
\(\small{ \ \displaystyle \frac{1}{3} \lt a \leqq 1 \ }\)のとき
最大値\(\small{ \ 2a\sqrt{a} \ (x=\sqrt{a}) \ }\)
最小値\(\small{ \ 0 \ (x=0) \ }\)