三次関数と直線の対称性と位置関係

こんにちは、リンス(@Lins016)です。
今回は三次関数と直線の対称性について学習していこう。

三次関数と直線の位置関係と対称性

三次関数のグラフは変曲点って呼ばれる点について対称なのは以前の記事で勉強したから理解してるよね。まだ読んでない人は先にそっちの記事を読んでね。

今回は三次関数のグラフだけじゃなく、三次関数と交わる直線についても一緒に対称性を考えてみよう。

三次関数と直線の対称性

三次関数と直線の共有点と解と係数の関係

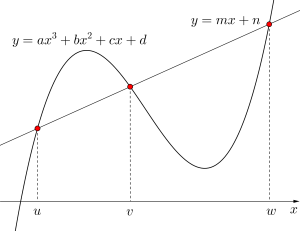
\(\small{ \ y=ax^3+bx^2+cx+d \ }\)と\(\small{ \ y=mx+n \ }\)の共有点が3つある場合について考えていこう。

曲線と直線の共有点の\(\small{ \ x \ }\)座標は
\(\small{ \ ax^3+bx^2+cx+d=mx+n \ }\)の解になるよね。

この方程式を整理して
\(\small{ \ ax^3+bx^2+(c-m)x+d-n=0 \ }\)

この方程式の解を\(\small{ \ x=u, \ v, \ w \ }\)とすると
解と係数の関係から
\(\small{ \ u+v+w=-\displaystyle\frac{b}{a} \ }\)が成り立つ。

この解と係数の関係の式の右辺には直線の方程式を定める\(\small{ \ m, \ n \ }\)が入っていなよね。

つまり三次関数\(\small{ \ y=ax^3+bx^2+cx+d \ }\)と直線\(\small{ \ y=mx+n \ }\)の共有点の\(\small{ \ x \ }\)座標の和は直線の方程式によらず常に一定になるってことなんだ。

次はこれを利用して直線\(\small{ \ y=mx+n \ }\)が三次関数\(\small{ \ y=ax^3+bx^2+cx+d \ }\)の変曲点を通る場合について考えてみよう。

三次関数と変曲点を通る直線との位置関係

さっきと同じように曲線と直線の共有点を求める方程式をたてよう。
\(\small{ \ ax^3+bx^2+(c-m)x+d-n=0 \ }\)
この解を\(\small{ \ x=p, \ q, \ r \ }\)とする。
ここで変曲点の\(\small{ \ x \ }\)座標を\(\small{ \ q \ }\)としておこう。

解と係数の関係から
\(\small{ \ p+q+r=-\displaystyle\frac{b}{a} \ }\)が成り立つ。

三次関数のグラフは変曲点に対して対称だから、
\(\small{ \ \displaystyle\frac{p+r}{2}=q \ }\)になるよね。

\(\small{ \ p+r=2q \ }\)になって、これを解と係数の関係式に代入すると
\(\small{ \ 3q=-\displaystyle\frac{b}{a} \ }\)

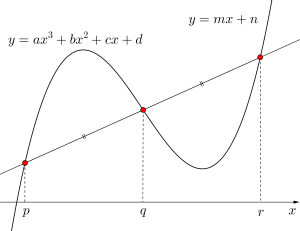
つまり\(\small{ \ -\displaystyle \frac{b}{a} \ }\)の値はどんな直線(変曲点を通らない直線)でも三次関数のグラフと三つの共有点を持つ場合は、常に変曲点の\(\small{ \ x \ }\)座標の\(\small{ \ 3 \ }\)倍になるってことなんだ。

三次関数の極値と変曲点との位置関係

次に極小を通り\(\small{ \ x \ }\)軸に平行な直線\(\small{ \ y=k \ }\)との共有点について考えてみよう。

極小値の\(\small{ \ x \ }\)座標を\(\small{ \ \beta \ }\)、曲線と直線の共有点で極小でない点の\(\small{ \ x \ }\)座標を\(\small{ \ s \ }\)とすると
\(\small{ \ ax^3+bx^2+cx+d=k \ }\)の解は
\(\small{ \ x=\beta, \ s \ }\)になるよね。

ここで解と係数の関係で\(\small{ \ \beta \ }\)は重解だってことに注意すると、
\(\small{ \ 2\beta+s=-\displaystyle \frac{b}{a} \ }\)

さらに
\(\small{ \ -\displaystyle \frac{b}{a}=3q \ }\)だから
\(\small{ \ 3q=2\beta+s \ }\)

これを変形すると
\(\small{ \ q-s=2(\beta-q) \ }\)

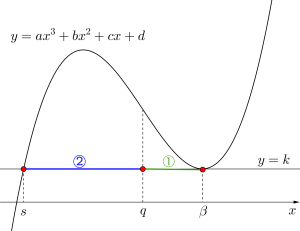
これは曲線と直線の共有点で極小でない点の\(\small{ \ x \ }\)座標から変曲点の\(\small{ \ x \ }\)座標までの距離が、極小の\(\small{ \ x \ }\)座標から変曲点の\(\small{ \ x \ }\)座標までの距離の\(\small{ \ 2 \ }\)倍になるってことを示しているんだ。

同様に極大を通り\(\small{ \ x \ }\)軸に平行な直線\(\small{ \ y=k \ }\)との共有点について考えてみよう。

極大値の\(\small{ \ x \ }\)座標を\(\small{ \ \alpha \ }\)、曲線と直線の共有点で極大でない点の\(\small{ \ x \ }\)座標を\(\small{ \ t \ }\)とすると
\(\small{ \ ax^3+bx^2+cx+d=k \ }\)の解は
\(\small{ \ x=\alpha, \ t \ }\)になるよね。

ここで解と係数の関係で\(\small{ \ \alpha \ }\)は重解ってことに注意すると、
\(\small{ \ 2\alpha+s=-\displaystyle \frac{b}{a} \ }\)

さらに
\(\small{ \ -\displaystyle \frac{b}{a}=3q \ }\)だから
\(\small{ \ 3q=2\alpha+t \ }\)

これを変形すると
\(\small{ \ 2(q-\alpha)=t-q \ }\)

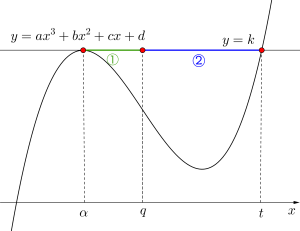
これは曲線と直線の共有点で極大でない点の\(\small{ \ x \ }\)座標から変曲点の\(\small{ \ x \ }\)座標までの距離が、極大の\(\small{ \ x \ }\)座標から変曲点の\(\small{ \ x \ }\)座標までの距離の\(\small{ \ 2 \ }\)倍になるってことを示しているんだ。

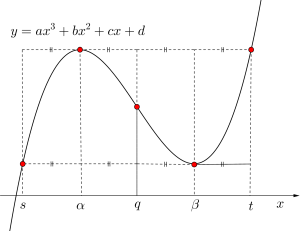
このことから図のように\(\small{ \ s, \ \alpha, \ q, \ \beta, \ t \ }\)は\(\small{ \ x \ }\)軸上を四等分することが言える。

これはどんな三次関数でも成り立つから覚えておこう。

三次関数と接線の共有点と接線の位置関係

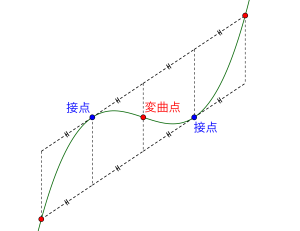
これを応用すると図のように曲線上の点から接線を引いた、接線と曲線の共有点と変曲点の位置関係にも使える。

曲線と接線が接点以外で交わる点と変曲点の\(\small{ \ x \ }\)座標の差は、接点と変曲点の\(\small{ \ x \ }\)座標の差の\(\small{ \ 2 \ }\)倍になるってことも上のやり方と同じで解と係数の関係から言えるからね。

今回問題は用意していないけど、三次関数のグラフの性質として学んだことは常に頭の片隅に置いておこう。

Point　三次関数と直線の対称性と位置関係

①変曲点と極大極小は対称で、極値を通る直線と三次関数の共有点にも位置関係が存在する
②接点と接線の接点以外の共有点と変曲点の位置関係は\(\small{ \ 1:2 \ }\)の関係