こんにちは、リンス(@Lins016)です。
今回は媒介変数で表された軌跡について学習していこう。
軌跡の問題では最頻出「媒介変数表示の軌跡」
今回学習する媒介変数で表された軌跡が軌跡の問題の中でも最も入試に出題されるパターンだから、今回きちんと解法を覚えておこう。
求める軌跡の点の座標を
\(\small{ \ (x, \ y)=( \ f(t), \ g(t) \ ) \ }\)のように媒介変数で表し、媒介変数\(\small{ \ t \ }\)を消去する
媒介変数の問題は、「\(\small{ \ t \ }\)の値が変化するとき」などの言い方がされているから、注意して問題文を読もう。
求める点を媒介変数で表して、媒介変数を消去する
「\(\small{ \ t \ }\)の値が変化するとき」のように、ある文字の値が変化することによって点が動き、その点の集まりが線になって軌跡になるから、まずは求める軌跡の座標\(\small{ \ (x, \ y) \ }\)を、その変化する文字で表すところから始めよう。
この変化する文字のことを媒介変数って言うからその名前も覚えておこう。パラメータって言い方もあるからね。
求める軌跡の点が\(\small{ \ (x, \ y)=( \ }\)媒介変数を用いた式、媒介変数を用いた式\(\small{ \ ) }\)っておけたら、この式から、媒介変数を消去して、つまり『媒介変数\(\small{=x, \ y}\)の式』に変形してこれを、もう一つの式に代入して、媒介変数を消去して\(\small{ \ x, \ y \ }\)だけの式にして軌跡を導こう。
\(\small{a \ }\)の値が変化するとき、放物線\(\small{ \ C:y=x^2-ax-2a-3 \ }\)、の頂点の軌跡を求めよ。
求める頂点を点\(\small{ \ \mathrm{P} \ }\)、座標を\(\small{ \ (x, \ y) \ }\)とおく。
まずは放物線を平方完成して頂点を求めると、
\(\small{\begin{eqnarray}y&=&x^2-ax-2a-3\\
&=&\left(x-\displaystyle \frac{a}{2}\right)^2-\displaystyle \frac{a^2}{4}-2a-3 \end{eqnarray}}\)
\(\small{(x,y)=\left(\displaystyle \frac{a}{2},-\frac{a^2}{4}-2a-3\right)}\)
\(\small{x=\displaystyle \frac{a}{2}}\)より\(\small{a=2x}\)、
これを\(\small{ \ y=-\displaystyle \frac{a^2}{4}-2a-3}\)に代入
\(\begin{eqnarray}\small{ y}&=&\small{-\displaystyle \frac{(2x)^2}{4}-2(2x)-3}\\
&=&\small{-x^2-4x-3} \end{eqnarray}\)


Point 媒介変数で表された軌跡の方程式
①求める軌跡の点を媒介変数で表わす
②媒介変数を消去して軌跡を求める
\(\small{ \ a \ }\)を実数とする。\(\small{ \ xy \ }\)平面において、関数\(\small{ \ y=x^2 \ }\)と\(\small{ \ y=-x^2+2ax-a \ }\)のグラフをそれぞれ\(\small{ \ C_1 \ }\)、\(\small{C_2 \ }\)とするとき以下の問いに答えよ。
(1)\(\small{ \ C_1 \ }\)と\(\small{ \ C_2 \ }\)が共有点を持たないような\(\small{ \ a \ }\)の範囲を求めよ。
(2)\(\small{ \ a \ }\)が(1)で求めた範囲にあるとき、\(\small{ \ C_1 \ }\)と\(\small{ \ C_2 \ }\)の両方に接する直線が\(\small{ \ 2 \ }\)本存在することを示せ。
(3)\(\small{ \ a \ }\)が(1)で求めた範囲を動くとき、\(\small{ \ C_1 \ }\)と\(\small{ \ C_2 \ }\)の両方に接する\(\small{ \ 2 \ }\)本の直線の交点が描く図形を図示せよ。
(1)\(\small{ \ C_1:y=x^2\cdots① \ }\)
\(\small{ \ C_2:y=-x^2+2ax-a\cdots② \ }\)より
\(\small{ \ x^2=-x^2+2ax-a \ }\)
\(\small{ \ 2x^2-2ax+a=0 \ }\)
共有点を持たないためには判別式\(\small{ \ D_1 \lt 0 \ }\)より
\(\small{ \ (2a)^2-4\cdot2\cdot a \lt 0 \ }\)
\(\small{ \ a(a-2) \lt 0 \ }\)
\(\small{ \ \therefore 0 \lt a \lt 2 \ }\)
(2)\(\small{①}\)上の\(\small{ \ (t, \ t^2) \ }\)における接線は\(\small{ \ y'=2x \ }\)より
\(\small{ \ y=2t(x-t)+t^2=2tx-t^2 \ }\)
これが\(\small{②}\)に接すればよいので
\(\small{ \ -x^2+2ax-a=2tx-t^2 \ }\)
\(\small{ \ x^2+2(t-a)x-t^2+a=0 \ }\)
この二次方程式の判別式\(\small{ \ D_2=0 \ }\)となればよいので
\(\small{ \ 4(t-a)^2-4(-t^2+a)=0 \ }\)
\(\small{ \ 2t^2-2at+a^2-a=0\cdots③ \ }\)
\(\small{③}\)の判別式は
\(\small{ \ D_3=4a^2-4\cdot2\cdot(a^2-a)=-4a(a-2) \ }\)となり
\(\small{ \ 0 \lt a \lt 2 \ }\)のとき\(\small{ \ D_3 \gt 0 \ }\)
よって\(\small{③}\)に異なる実数解が\(\small{ \ 2 \ }\)つあるから\(\small{①②}\)に両方接する直線が\(\small{ \ 2 \ }\)本存在する。
(3)\(\small{③}\)に異なる実数解を\(\small{ \ \alpha \ }\)、\(\small{ \ \beta \ }\)とすると、2本の接線は
\(\small{ \ y=2\alpha x-\alpha^2 \ }\)と\(\small{ \ y=2\beta x-\beta^2 \ }\)
この2直線の交点は\(\small{ \ 2\alpha x-\alpha^2=2\beta x-\beta^2 \ }\)
\(\small{ \ \alpha \neq \beta \ }\)より\(\small{ \ x=\displaystyle \frac{\alpha +\beta}{2} \ }\)
このとき\(\small{ \ y=\alpha \beta \ }\)
\(\small{③}\)の解と係数の関係より
\(\small{ \ \alpha + \beta=a \ }\)、\(\small{ \ \alpha \beta=\displaystyle \frac{a^2-a}{2} \ }\)
となるから
\(\small{ \ (x, \ y)=\left(a, \ \displaystyle \frac{a^2-a}{2} \right) \ }\)
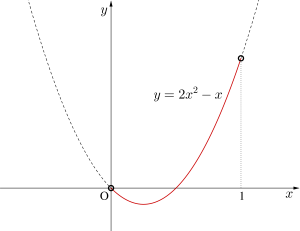
\(\small{ \ a \ }\)を消去して、\(\small{ \ y=2x^2-x \ }\)を満たす。
ただし\(\small{ \ 0 \lt a \lt 2 \ }\)より\(\small{ \ 0 \lt x \lt 1 \ }\)
したがって交点の描く図形は図の赤線部分である。