こんにちは、リンス(@Lins016)です。
今回は空間図形の書き方のコツについて話をしていこう。
空間図形の書き方のコツ
空間図形って\(\small{ \ xyz \ }\)方向を持つ三次元だよね。それを平面の紙(二次元)に書こうっていうんだから、そもそも無理があるよね。
それでも問題を解く上で図形を描いて解いていく方が頭の中で想い描いて考えるより、視認性に優れて解きやすくなるから、図形を描くことはとても大切って言えるよね。
それじゃ今回はなかなか綺麗に描けない空間図形を少しでも綺麗に描けるように練習してみよう。
実線と破線の使い分け
これがまず\(\small{ \ 1 \ }\)番のポイントだけど、「手前の線は実線で、奥の線は破線で描く」ってこと。
手前の線っていうのは実物の図形があって見えている線ってことね。それに対して奥の線ってのは実物では裏に回って見ないと見えない線のこと。
教科書や参考書、問題集など、ありとあらゆる書籍はこのポイントを利用して図形が描いてある。もちろん問題や条件によってこの限りじゃないけど、まず大抵の場合こうなってる。
自分の持ってる教科書の空間ベクトルに描かれてる図形を見て確認してみよう。
全て実線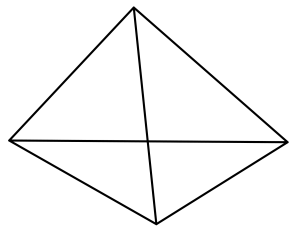
手前実線・奥破線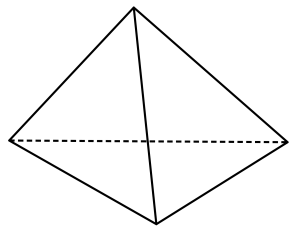
全て実線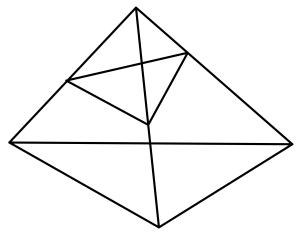
手前実線・奥破線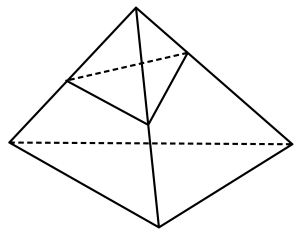
全て実線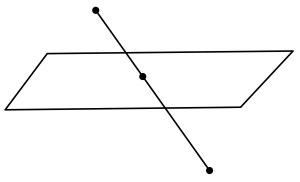
手前実線・奥破線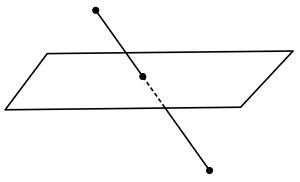
まずはこの「手前の線は実線で、奥の線は破線で描く」を実践しよう。これだけでだいぶ空間図形らしくなるからね。
どこから見た図形を書くか
図形を描くときにどこから見た図を描くかってことも重要だよね。
例えば\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸、\(\small{ \ z \ }\)軸を取ったとき立体的な図形も必要だし、平面的な図形も必要になる場合もあるよね。
全体を見わたす位置から見た図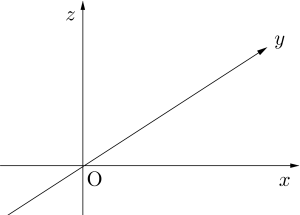
\(\small{ \ z \ }\)軸方向から見た図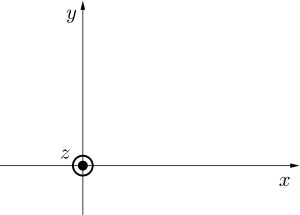
この図形の書き方は数学Ⅲの積分の「ある軸について回転させてできる回転体の体積を求める問題」を解くときに利用することが多いかな。
体積の問題じゃなくても、複雑な図形だと簡単に全体図を描くことが難しい場合、断面図や横から見た平面図を描いて問題を考えることも多いからね。
もちろん見る方向を変更してもいいから、\(\small{ \ y \ }\)軸に回転させるときは\(\small{ \ y \ }\)軸方向から見たりもするからね。
\(\small{ \ y \ }\)軸方向から見た図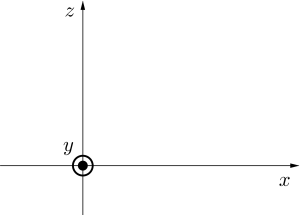
もちろん全体を見渡す図だってどの方向から描けば解きやすいかっていうのもまったく関係なくはないよね。
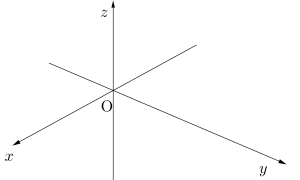
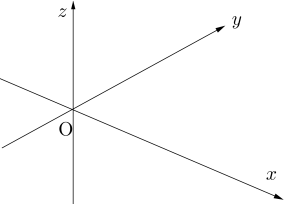
ただこの全体を見渡す図を描くのって本当に難しいから、どこの方向から描けばいいかっていうのは余裕があれば考えてみてもいいけど、問題を解く上で、とりあえずは適当で構わないからね。
解いていく上で少し見づらくなったら角度を変えて書き直してみよう。
成分表示に軸が必要か
次に「空間ベクトルの成分表示の問題」の場合について考えていこう。
空間座標が与えられるとある程度正確に点を描きたくなるけど、それって必要かな。
例えば、\(\small{ \ x \ }\)軸、\(\small{ \ y \ }\)軸、\(\small{ \ z \ }\)軸を描いて、簡単な目盛りを記して、座標を描くってなると結構描くの大変だよね。
しかもそんな正確な図を描かないと解けない問題が出題されることはないから、大体の図が描けたらそれでいいんだ。
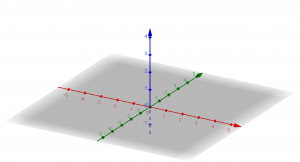
しかも座標軸って実はそんなに必要じゃなかったりするからね。むしろ軸を描いたせいで図が見づらくなって混乱する可能性だってあるよね。
だから空間ベクトルの成分表示の場合、座標軸って必ず描かなくても問題ないからね。
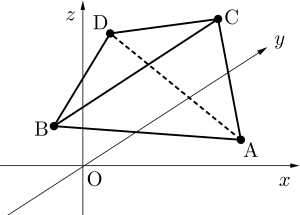
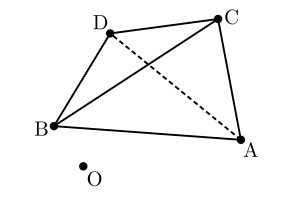
上の図を見比べて、座標軸が必要だってこともないよね。
ちなみにこの「座標軸が必要ない」っていうのはあくまで僕の主観だからね。もちろん絶対描きなさいって先生もいると思うけどね・・・・。

普段の問題演習から意識して、なるべく問題を解く上で参考になるような図を描こう。
問題の解答解説を確認するときも、図形がどんな風に描かれているかも意識して確認しておこう。

