こんにちは、リンス(@Lins016)です。
今回は整数の約数の個数と総和とその応用について学習していこう。
整数の約数
整数の約数についての問題は、約数の個数や約数の和なんか有名だよね。それが以外にも約数の考え方を利用する問題って色々あるから、今回はそんな問題を考えながら約数について勉強していこう。

かぶってる部分が多いけど、整数の分野の問題としてきちんと学習していこう。
・約数
整数\(\small{ \ a \ }\)によって整数\(\small{ \ b \ }\)が割り切れるとき、\(\small{ \ a \ }\)は\(\small{ \ b \ }\)の約数であるという
・素数
\(\small{ \ 1 \ }\)とその数自身以外に正の約数を持たない整数のこと
・因数
ある整数がいくつかの整数の積で表されるとき、その積のそれぞれの整数のこと
・合成数
\(\small{ \ 1 \ }\)とその数以外の約数をもつ整数のこと。
\(\small{ \ 2 \ }\)つ以上の素数の積の形で表すことができる整数
・約数の個数
\(\small{ \ n=2^p\cdot3^q\cdot5^r\cdots \ }\)のとき
\(\small{ \ (p+1)(q+1)(r+1)\cdots \ }\)
・約数の総和
\(\small{ \ n=2^p\cdot3^q\cdot5^r\cdots \ }\)のとき
約数とは
約数って小学生のとき教わると思うけど、「整数\(\small{ \ a \ }\)によって整数\(\small{ \ b \ }\)が割り切れるとき、\(\small{ \ a \ }\)は\(\small{ \ b \ }\)の約数である」ってことだったよね。
これを更にもう一歩進めると、「整数\(\small{ \ b \ }\)を整数\(\small{ \ a \ }\)で割ったときの商も\(\small{ \ b \ }\)の約数である」って言えるからね。
つまり\(\small{ \ b=ka \ }\)(\(\small{ \ k \ }\)は整数)のとき、\(\small{ \ k, \ a \ }\)ともに\(\small{ \ b \ }\)の約数であるってことなんだ。
当たり前のことだけど、再度確認しておこう。
だから\(\small{ \ 24 \ }\)の約数は\(\small{ \ 1, \ 2, \ 3, \ 4, \ 6, \ 8, \ 12, \ 24 \ }\)になる。
これって\(\small{ \ 2 \ }\)つの数を外側から掛けていくと\(\small{ \ 24 \ }\)になるのが分かるよね。
\(\small{ \ 24 \ }\)の約数は\(\small{ \ 1, \ 2, \ 3, \ 4, \ \displaystyle\frac{24}{4}, \ \displaystyle\frac{24}{3} , \ \displaystyle\frac{24}{2}, \ \displaystyle\frac{24}{1} \ }\)になるってことなんだ。

じゃあ負の約数はないのかっていうとないわけじゃないけど、この範囲では正の約数のみ考えるってことになるかな。ちょっと曖昧だけどね。
素因数分解
ある整数の約数の個数や和を求めるには、まずその整数を素因数分解する必要がある。
素因数分解っていうの中学で教わったと思うけど、その整数を素数の積の形で表すことだよね。
素数は「\(\small{ \ 1 \ }\)とその数自身以外に正の約数を持たない整数」のこと。
因数は「ある整数がいくつかの整数の積で表されるとき、その積のそれぞれの整数」のこと。
このそれぞれの整数、つまり因数は約数でもあるからね。
ちなみに因数は整数だけじゃなく文字式を積の形に表すこともあるよね。これを因数分解っていうことは知ってるよね。
また素数でない整数、つまり\(\small{ \ 1 \ }\)とその数以外の約数を持つ整数を合成数っていうからね。
さらに素数である因数を素因数っていうよね。だから素因数分解はある自然数を素数だけの積の形で表すことで、積の順序を考えなければ\(\small{ \ 1 \ }\)通りしかない。
ちなみにこのことを「素因数分解の一意性」っていうんだ。まぁ~確かに何通りもあるわけないよね。
ある自然数の約数の個数や約数の総和を求めるために素早くを素因数分解しよう。
約数の個数
次に約数の個数について具体的に考えてみよう。
例えば\(\small{ \ 360 \ }\)の約数の個数を考える。
このとき\(\small{ \ 360 \ }\)を素因数分解すると\(\small{ \ 360=2^3\cdot3^2\cdot5 \ }\)になるよね。
つまり\(\small{ \ 360 \ }\)は素因数\(\small{ \ 2 \ }\)を\(\small{ \ 3 \ }\)個、素因数\(\small{ \ 3 \ }\)を\(\small{ \ 2 \ }\)個、素因数\(\small{ \ 5 \ }\)を\(\small{ \ 1 \ }\)個使った数になる。
ここで約数は\(\small{ \ 360 \ }\)を割り切れる数になるので、素因数を使って表せる数と素因数を使わないで表せる数ということになる。
つまり
素因数\(\small{ \ 2 \ }\)を使って表せる数は\(\small{ \ 2^1, \ 2^2, \ 2^3 \ }\)の\(\small{ \ 3 \ }\)通り
素因数\(\small{ \ 3 \ }\)を使って表せる数は\(\small{ \ 3^1, \ 3^2 \ }\)の\(\small{ \ 2 \ }\)通り
素因数\(\small{ \ 5 \ }\)を使って表せる数は\(\small{ \ 5^1 \ }\)の\(\small{ \ 1 \ }\)通り
これに素因数を使わずに表せる数がそれぞれ\(\small{ \ 1 \ }\)通りずつ(\(\small{ \ 2^0, \ 3^0, \ 5^0 \ }\))ある。
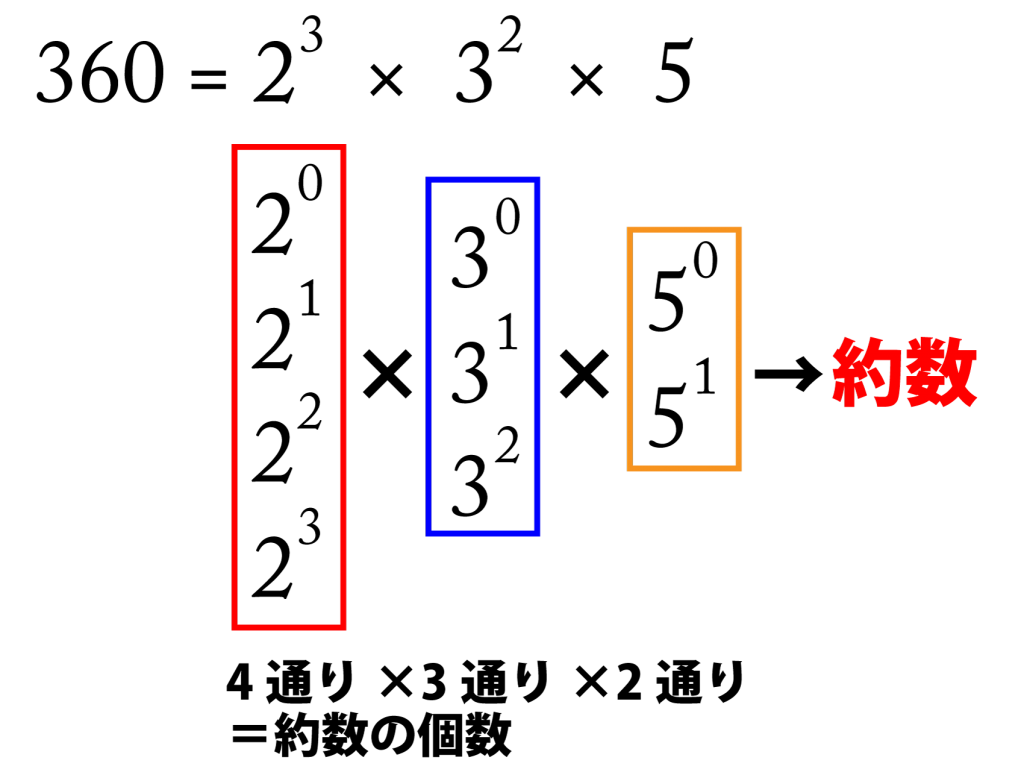
これらを組み合わせた個数だけ約数はあるから
約数の個数は\(\small{ \ (3+1)\times(2+1)\times(1+1)=24 \ }\)通りあるんだ。
これを一般化すると
\(\small{ \ n=2^p\cdot3^q\cdot5^r\cdot7^s\cdots \ }\)のとき
約数の個数は\(\small{ \ (p+1)(q+1)(r+1)(s+1)\cdots \ }\)って表すことができる。
だから約数の個数を求めるときはすぐに素因数分解しよう。
約数の総和
次に約数の総和について具体的に考えてみよう。
上の続きで\(\small{ \ 360 \ }\)の約数の総和を考える。
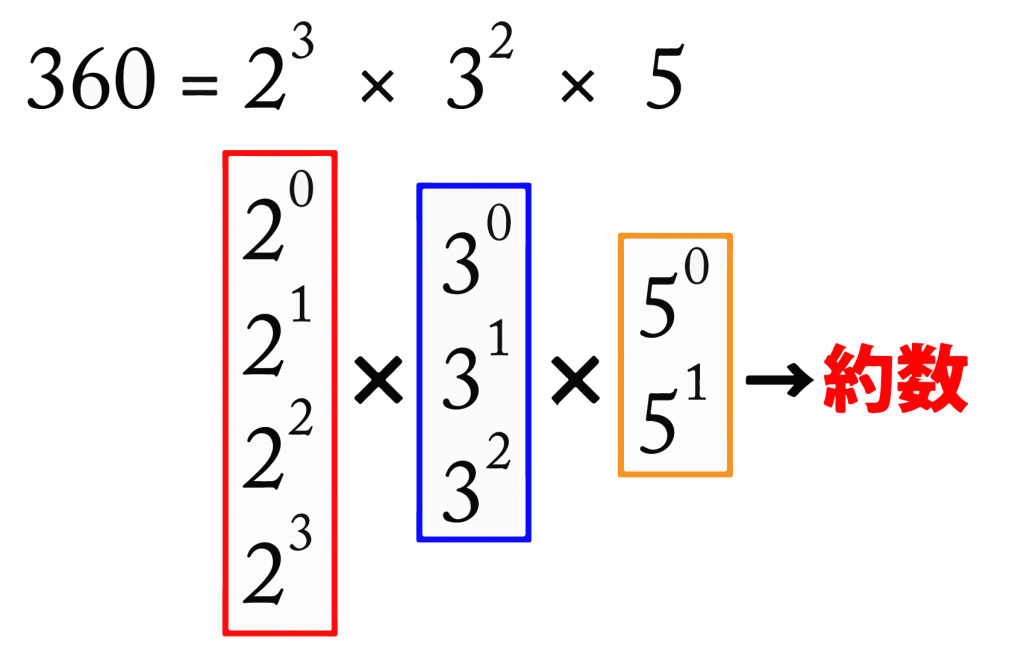
約数は\(\small{ \ 2^0\times3^0\times5^0 \ }\)や\(\small{ \ 2^2\times3^1\times5^1 \ }\)など赤の枠から\(\small{ \ 1 \ }\)個、青の枠から\(\small{ \ 1 \ }\)個、オレンジの枠から\(\small{ \ 1 \ }\)個とって掛け合わせたものになるよね。
掛け合わせたものをを全部足せばいいから、その式は
\(\small{\begin{eqnarray}&&(2^0+2^1+2^2+2^3)(3^0+3^1+3^2)(5^0+5^1)\\
&=&1170 \ \end{eqnarray}}\)
これを一般化すると
\(\small{ \ n=2^p\cdot3^q\cdot5^r\cdots \ }\)のとき
になるんだ。
だから約数の総和も素因数分解して求めよう。
\(\small{ \ 240 \ }\)の約数について答えよ。
(1)約数の個数を求めよ。
(2)約数の総和を求めよ。
(3)約数を全てかけた値を求めよ。
(1)\(\small{ \ 240 \ }\)を素因数分解すると
\(\small{ \ 240=2^4\times3\times5 \ }\)
よって約数の個数は
\(\small{ \ (4+1)(1+1)(1+1)=20 \ }\)
(2)約数の総和は
\(\small{ \ =744 \ }\)
(3)\(\small{ \ a \ }\)という約数があれば、\(\small{ \ \displaystyle\frac{240}{a} \ }\)も約数だから、この\(\small{ \ 2 \ }\)つをかけると\(\small{ \ 240 \ }\)になる。
約数は全部で\(\small{ \ 20 \ }\)個あるから、かけて\(\small{ \ 240 \ }\)になるペアは\(\small{ \ 20\div2=10 \ }\)
よってもとめる答えは\(\small{ \ 240^{10} \ }\)

ちなみに約数の個数が奇数個の場合、元の数は平方数になる。
\(\small{ \ n=2^p\cdot3^q\cdot5^r \ }\)のとき約数の個数は\(\small{ \ (p+1)(q+1)(r+1) \ }\)でこれが奇数になるためには\(\small{ \ (p+1), \ (q+1), \ (r+1) \ }\)それぞれが奇数である必要があるよね。
つまり\(\small{ \ p, \ q, \ r \ }\)ともに偶数ってことになる。
\(\small{ \ p=2p', \ q=2q', \ r=2r' \ }\)とすると
\(\small{\begin{eqnarray} \ n&=&2^p\cdot3^q\cdot5^r\\
&=&2^{2p'}\cdot3^{2q'}\cdot5^{2r'}\\
&=&\left(2^{p'}\cdot3^{q'}\cdot5^{r'}\right)^2 \ \end{eqnarray}}\)
だから約数の個数が奇数個だったら、その整数は平方数になるんだ。大事なことだから覚えておこう。
Point 整数の約数の個数と総和とその応用
①約数の個数と総和は素因数分解から求める
②元の整数を約数で割った数も約数である
ある自然数の約数をすべて足すと\(\small{ \ 360 \ }\)になり、約数の逆数をすべて足すと\(\small{ \ 3 \ }\)になる。この元の自然数を求めよ。
自然数の約数を\(\small{ \ a_1, \ a_2, \ \cdots, \ a_k \ }\)とする。
題意より
\(\small{ \ a_1+a_2+ \cdots+a_k=360\cdots① \ }\)
\(\small{ \ \displaystyle\frac{1}{a_1}+\displaystyle\frac{1}{a_2}+\cdots+\displaystyle\frac{1}{a_k}=3\cdots② \ }\)
ここで元の自然数を\(\small{ \ n \ }\)とすると\(\small{ \ ② \ }\)の両辺に\(\small{ \ n \ }\)をかけると
\(\small{ \ n\left(\displaystyle\frac{1}{a_1}+\displaystyle\frac{1}{a_2}+\cdots+\displaystyle\frac{1}{a_k}\right)=3n \ }\)
\(\small{ \ \displaystyle\frac{n}{a_1}+\displaystyle\frac{n}{a_2}+\cdots+\displaystyle\frac{n}{a_k} =3n \ }\)
\(\small{ \ a_k+a_{k-1}+\cdots+a_1=3n\cdots③ \ }\)
\(\small{ \ ①, \ ③ \ }\)より
\(\small{ \ 360=3n \ }\)
\(\small{ \ \therefore n=120 \ }\)

\(\small{ \ \left(\displaystyle\frac{1}{a_1}+\displaystyle\frac{1}{a_2}+\cdots+\displaystyle\frac{1}{a_k}\right) \times n\\[8pt] =\displaystyle\frac{n}{a_1}+\displaystyle\frac{n}{a_2}+\cdots+\displaystyle\frac{n}{a_k}\\[8pt] =a_k+a_{k-1}+\cdots+a_1 \ }\)

