こんにちは、リンス(@Lins016)です。
今回は指数関数の置換の仕方について学習していこう。
指数関数の二次式・三次式への置換
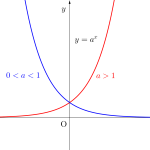
前回\(\small{ \ y=a^x \ }\)の指数関数のグラフを教わったけど、実際試験に出題される指数関数といえば\(\small{ \ 4^x+2^{x+2}=0 \ }\)のような方程式や\(\small{ \ y=9^x+9^{-x}+3^x+3^{-x}+3 \ }\)のような関数がほとんどなんだ。
今回はこういった方程式や関数を解く前に指数関数を置換するやり方について書いていこうと思う。
\(\small{ \ a^x=t \ }\)のとき
\(\small{ \ t^2=(a^2)^x=a^{2x}=(a^x)^2 \ }\)
\(\small{ \ t^3=(a^3)^x=a^{3x}=(a^x)^3 \ }\)
\(\small{ \ a^x+a^{-x}=t \ }\)のとき
\(\small{ \ a^{2x}+a^{-2x}=t^2-2 \ }\)
\(\small{ \ a^{3x}+a^{-3x}=t^3-3t \ }\)
指数関数の問題
\(\small{ \ 4^x+2^{x+1}-8 \ }\)のような式を見たら、\(\small{ \ t=2^x \ }\)と置いて\(\small{ \ t^2+2t-8 \ }\)って二次式に変形するのが指数関数の置換なんだ。これが、\(\small{ \ t^2+2t-8=0 \ }\)ってなれば二次方程式だし、\(\small{ \ y=t^2+2t-8 \ }\)ってなれば二次関数になるよね。
もちろん\(\small{ \ 8^x+2^{x+1}-8 \ }\)ってなっていれば\(\small{ \ t^3+2t-8 \ }\)ってなって三次式になるから、三次関数なら微分するし、三次方程式なら因数定理から解を求めるからね。
つまり指数関数って言っても置換して二次関数や二次方程式、場合によっては三次関数や三次方程式にするっていうのがほとんどなんだ。
指数関数の置換は大きく分けて\(\small{ \ 2 \ }\)つある。それは\(\small{ \ a^x \ }\)を\(\small{ \ t \ }\)って置換するパターンと\(\small{ \ a^x+a^{-x} \ }\)を\(\small{ \ t \ }\)って置換するパターンなんだ。
指数関数の置換 その1
まずは\(\small{ \ t=a^x \ }\)って置換する場合について考えてみよう。これを利用するのは\(\small{ \ 4^x+2^{x+1}-8 \ }\)のような式のとき。
\(\small{ \ t=2^x \ }\)を二乗すると\(\small{ \ t^2=(2^x)^2=2^{2x}=4^x \ }\)になる。つまり「\(\small{ \ 4^x \ }\)や\(\small{ \ 2^{2x} \ }\)を見たら\(\small{ \ 2^x \ }\)の二乗だ」って気付かないといけないってこと。
\(\small{ \ 2^x \ }\)を\(\small{ \ t \ }\)って置いて\(\small{ \ x \ }\)の式から\(\small{ \ t \ }\)の式に変えたいって考えるわけだから\(\small{ \ 2^{x+2}=2^x\cdot2^2=4t \ }\)になるし、\(\small{ \ 2^{x-2}=2^x\cdot2^{-2}=\displaystyle\frac{1}{4}t \ }\)ってなるからね。
この考え方を使って\(\small{ \ 4^x+2^{x+1}-8 \ }\)を\(\small{ \ t^2+2t-8 \ }\)に置換しよう。
そうなると後は二次関数や二次方程式、二次不等式の問題になるからね。
よく間違えてる人に\(\small{ \ 4^x+2^{x+1}-8 \ }\)の式を\(\small{ \ 2^{2x}+2^{x+1}-2^3 \ }\)ってしちゃう人がいるけど、これは意味ないからね。\(\small{ \ 2^x \ }\)を\(\small{ \ t \ }\)って置換して二次式にしたいっていうのが目標だからね。
もちろん\(\small{ \ t=2^x \ }\)を三乗すると\(\small{ \ t^3=(2^x)^3=2^{3x}=8^x \ }\)になるから、\(\small{ \ 8^x \ }\)や\(\small{ \ 2^{3x} \ }\)を見たら\(\small{ \ 2^x \ }\)の三乗だから\(\small{ \ t=2^x \ }\)として\(\small{ \ t \ }\)の三次関数や三次方程式に変形するようにしよう。
指数関数の置換 その2
次に\(\small{ \ t=a^x+a^{-x} \ }\)って置換する場合について考えてみよう。\(\small{ \ t \ }\)を二乗すると
\(\small{\begin{eqnarray} \ t&=&\left(a^x+a^{-x}\right)^2\\
&=&(a^x)^2+2\cdot a^x\cdot a^{-x}+(a^{-x})^2\\
&=&a^{2x}+2+a^{-2x} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \therefore a^{2x}+a^{-2x}&=&\left(a^x+a^{-x}\right)^2-2\\
&=&t^2-2 \ \end{eqnarray}}\)
だから\(\small{ \ 4^x+4^{-x}+2^x+2^{-x}-4 \ }\)って式を見たら\(\small{ \ t=2^x+2^{-x} \ }\)って置換して\(\small{ \ t^2+t-6 \ }\)って\(\small{ \ x \ }\)の式から\(\small{ \ t \ }\)の式に変形しよう。もちろん\(\small{ \ 4^x+4^{-x} \ }\)は\(\small{ \ 2^{2x}+2^{-2x} \ }\)になっている場合もあるからね。
さらに\(\small{ \ t=2^x+2^{-x} \ }\)を三乗してみよう。
&=&(2^x)^3+3(2^x)^2\cdot 2^{-x}+3\cdot2^x\cdot (2^{-x})^2+(2^{-x})^3\\
&=&2^{3x}+3\cdot2^x+3\cdot2^{-x}+2^{-3x}\\
&=&2^{3x}+2^{-3x}+3t \ \end{eqnarray}}\)
だから\(\small{ \ 2^{3x}+2^{-3x}=t^3-3t \ }\)になるんだ。もちろん\(\small{ \ 2^{3x}+2^{-3x} \ }\)は\(\small{ \ 8^x+8^{-x} \ }\)とも書けるからね。
この\(\small{ \ 4^x+4^{-x} \ }\)や\(\small{ \ 8^x+8^{-x} \ }\)を見たら\(\small{ \ t=2^x+2^{-x} \ }\)って置換して問題を解こう。
指数関数の置換と範囲
高校数学で非常に大事なことがある。それは「\(\small{ \ t=x}\)の式」って置換したときは範囲が必ず変化するっていうこと。
\(\small{ \ t=2^x \ }\)って置換すると指数関数のグラフから\(\small{ \ t\gt0 \ }\)になるよね。だから\(\small{ \ x \ }\)の式を\(\small{ \ t \ }\)の式に置換したとき\(\small{ \ t\gt0 \ }\)の範囲で問題を考えないといけないんだ。
-

指数関数のグラフとその利用
指数関数のグラフやグラフを利用した大小関係の問題について詳しく解説しています。
続きを見る
さらに\(\small{ \ t=2^x+2^{-x} \ }\)なら\(\small{ \ 2^x\gt0, \ 2^{-x}\gt0 \ }\)だから相加平均と相乗平均の関係を使って
\(\small{ \ t=2^x+2^{-x}\geqq2\sqrt{2^x\cdot2^{-x}}=2 \ }\)になるから\(\small{ \ t\geqq2 \ }\)になるんだ。
-

相加平均と相乗平均
相加平均と相乗平均の関係の証明について解説しています。。
続きを見る
置換したとき、範囲が変わることを忘れないようにしよう。
整数乗と分数乗
\(\small{ \ a^x \ }\)と\(\small{ \ a^{\frac{1}{2}x}\ }\)って\(\small{ \ a^x \ }\)を\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗したら\(\small{ \ a^{\frac{1}{2}x}\ }\)になるって考えられるよね。
でも高校数学では\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗ってあまり使わない。どういうことかっていうと、展開の公式って二乗や三乗する公式しかないよね。つまり整数乗するっていうのが基本なんだ。だから\(\small{ \ a^x \ }\)と\(\small{ \ a^{\frac{1}{2}x}\ }\)をみたら『\(\small{ \ a^x \ }\)を\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗したら\(\small{ \ a^{\frac{1}{2}} \ }\)』って考えるんじゃなくて、『\(\small{ \ a^{\frac{1}{2}} \ }\)を二乗したら\(\small{ \ a^x \ }\)』って考えたいんだ。
\(\small{ \ a \ }\)の\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗は\(\small{ \ \sqrt{a} \ }\)ってなるから、まだそこまで問題じゃないけど、\(\small{ \ a, \ b \ }\)の式\(\small{ \ a^n+b^n \ }\)の形について考えると、問題が出てくる。
\(\small{ \ a^2+b^2=(a+b)^2-2ab \ }\)、\(\small{ \ a^3+b^3=(a+b)^3-3ab(a+b) \ }\)ってなるから\(\small{ \ a^n+b^n \ }\)の形は\(\small{ \ (a+b)^n \ }\)と基本対称式\(\small{ \ a+b, \ ab \ }\)を利用して表すことができるよね。
-

対称式
基本対称式の解説や定番の対称式を解説しています。
続きを見る
だけど\(\small{ \ a+b \ }\)の\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗は\(\small{ \ \sqrt{a}+\sqrt{b} \ }\)じゃなくて\(\small{ \ \sqrt{a+b} \ }\)になるから、そもそも\(\small{ \ a^n+b^n \ }\)の形にならないよね。
だから\(\small{ \ a+b \ }\)と\(\small{ \ \sqrt{a}+\sqrt{b} \ }\)をみたら『\(\small{ \ a+b \ }\)を\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗して\(\small{ \ \sqrt{a}+\sqrt{b} \ }\)を作る』じゃなくて『\(\small{ \ \sqrt{a}+\sqrt{b} \ }\)を二乗して\(\small{ \ a+b \ }\)を作る』って考えないといけないんだ。\(\small{ \ a+b \ }\)を\(\small{ \ \displaystyle\frac{1}{2} \ }\)乗しても\(\small{ \ \sqrt{a}+\sqrt{b} \ }\)は作れないからね。
\(\small{ \ t=\sqrt{a}+\sqrt{b} \ }\)とすると\(\small{ \ t^2=a+2\sqrt{ab}+b \ }\)になるから\(\small{ \ a+b=\left(\sqrt{a}+\sqrt{b}\right) ^2-2\sqrt{ab}\ }\)って表すことができるよね。

ちなみに\(\small{ \ a^x \ }\)は\(\small{ \ a \ }\)のべき乗って言って、特に\(\small{ \ x \ }\)が自然数のとき\(\small{ \ a \ }\)の累乗って言うからね。
\(\small{ \ 2^x+2^{-x}=t \ }\)のとき、次の値を\(\small{ \ t \ }\)を用いて表せ。
(1)\(\small{ \ 2^{2x}+2^{-2x} \ }\)
(2)\(\small{ \ 2^{3x}+2^{-3x} \ }\)
(3)\(\small{ \ 2^{\frac{1}{2}x}+2^{-\frac{1}{2}x} \ }\)
(1)
\(\small{ \ \left(2^x+2^{-x}\right)^2=2^{2x}+2^{-2x}+2 \ }\)より
\(\small{ \ \therefore2^{2x}+2^{-2x}=t^2-2 \ }\)
(2)
\(\small{\begin{eqnarray} \ t^3&=&\left(2^x+2^{-x}\right)^3\\
&=&2^{3x}+2^{-3x}+3(2^x+2^{-x}) \ \end{eqnarray}}\)より
\(\small{ \ \therefore2^{3x}+2^{-3x}=t^3-3\cdot t \ }\)
(3)
\(\small{ \ \left(2^{\frac{1}{2}x}+2^{-\frac{1}{2}x}\right)^2=2^x+2^{-x}+2 \ }\)
\(\small{ \ \therefore2^{\frac{1}{2}x}+2^{-\frac{1}{2}x}=\sqrt{t+2} \ }\)

もちろん\(\small{ \ 2^{\frac{1}{2}x}+2^{-\frac{1}{2}x} \ }\)に直接相加平均相乗平均の関係を使っても\(\small{ \ 2^{\frac{1}{2}x}+2^{-\frac{1}{2}x}\geqq2 \ }\)になるからね。
次の式を簡単にせよ。ただし、\(\small{ \ a\gt0, \ b\gt0 \ }\)とする。
(1)\(\small{ \ \left(x-y^{-1}\right)\div\left(x^{\frac{1}{2}}+y^{-\frac{1}{2}}\right) \ }\)
(1)
=\left(x^{\frac{1}{2}}+y^{-\frac{1}{2}}\right)\left(x^{\frac{1}{2}}-y^{-\frac{1}{2}}\right)\div\left(x^{\frac{1}{2}}+y^{-\frac{1}{2}}\right)\\
=x^{\frac{1}{2}}-y^{-\frac{1}{2}} \ }\)
(2)
=\left(a^{\frac{1}{2}}+b^{\frac{1}{2}}\right)^2-\left(a^{\frac{1}{4}}b^{\frac{1}{4}}\right)^2\\
=a+2a^{\frac{1}{2}}b^{\frac{1}{2}}+b-a^{\frac{1}{2}}b^{\frac{1}{2}}\\
=a+a^{\frac{1}{2}}b^{\frac{1}{2}}+b \ }\)

Point 指数関数の置換のやり方
①\(\small{ \ a^{2x} \ }\)と\(\small{ \ a^x \ }\)を含む式は\(\small{ \ t=a^x \ }\)とおく
②\(\small{ \ a^{2x}+a^{-2x} \ }\)と\(\small{ \ a^x+a^{-x} \ }\)を含む式は\(\small{ \ t=a^x+a^{-x} \ }\)とおく
③置換したら必ず範囲を考える
\(\small{ \ 2^x+2^{-x}=t \ }\)とする。
このとき\(\small{ \ 2^{nx}+2^{-nx} \ }\)は\(\small{ \ t \ }\)の式で表せることを示せ。ただし、\(\small{ \ n \ }\)は自然数とする。
数学的帰納法を用いて証明する
(i)\(\small{ \ n=1 \ }\)のとき
\(\small{ \ 2^x+2^{-x}=t \ }\)
よって\(\small{ \ n=1 \ }\)のとき成り立つ
\(\small{ \ n=2 \ }\)のとき
&=&t^2-2 \ \end{eqnarray}}\)
よって\(\small{ \ n=2 \ }\)のとき成り立つ
(ii)\(\small{ \ n=k, \ k+1 \ }\)のとき
\(\small{ \ 2^{kx}+2^{-kx} \ }\)と\(\small{ \ 2^{(k+1)x}+2^{-(k+1)x} \ }\)が\(\small{ \ t \ }\)の式になると仮定する
\(\small{ \ 2^{kx}+2^{-kx}=f_k(t) \ }\)
\(\small{ \ 2^{(k+1)x}+2^{-(k+1)x}=f_{k+1}(t) \ }\)とすると
&=&tf_{k+1}(t)-f_k(t) \ \end{eqnarray}}\)
よって\(\small{ \ n=k+2 \ }\)のときも成り立つ
(i)(ii)よりすべての自然数\(\small{ \ n \ }\)で
\(\small{ \ 2^{nx}+2^{-nx} \ }\)は\(\small{ \ t \ }\)の式で表せる

-

仮定が二つ必要な数学的帰納法の証明
どのような問題で二つの仮定が必要になるのか解説しています。
続きを見る