こんにちは、リンス(@Lins016)です。
今回は対数関数のグラフとその利用について学習していこう。
対数関数のグラフ
対数関数\(\small{ \ y=\log_ax \ }\)は底の大きさでグラフが全然違うよね。
\(\small{ \ a\gt1 \ }\)のときはグラフは単調増加、\(\small{ \ 0\lt a \lt 1 \ }\)のときグラフは単調減少になるからね。今回はグラフを利用した問題について考えていこう。
\(\small{ \ y=\log_ax \ }\)は\(\small{ \ (1, \ 0) \ }\)を通る
\(\small{ \ a\gt1 \ }\)ならグラフは単調増加
\(\small{ \ 0\lt a \lt1 \ }\)ならグラフは単調減少
\(\small{ \ \log_aM\lt \log_aN \ }\)のとき
\(\small{ \ a\gt1 \ }\)なら\(\small{ \ M\lt N \ }\)
\(\small{ \ 0\lt a\lt1 \ }\)なら\(\small{ \ M\gt N \ }\)
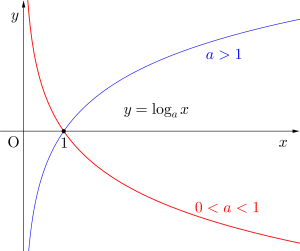
対数関数のグラフ
対数関数\(\small{ \ y=\log_ax \ }\)のグラフについて考えてみよう。\(\small{ \ x=1 \ }\)のとき\(\small{ \ y=\log_a1=0 \ }\)だから『\(\small{ \ y=\log_ax \ }\)のグラフは\(\small{ \ a \ }\)の値に関わらず\(\small{ \ (1, \ 0) \ }\)を通る』って言えるよね。
まずは底が\(\small{ \ 1 \ }\)より大きい\(\small{ \ y=\log_2x \ }\)のグラフについて見ていこう。
\(\small{ \ x=1, \ 2, \ 2^2, \ 2^3,\cdots \ }\)と\(\small{ \ x \ }\)が大きくなると\(\small{ \ y=0, \ 1, \ 2, \ 3,\cdots \ }\)って\(\small{ \ y \ }\)も大きくなるよね。
\(\small{ \ x \ }\)の増加量に対して\(\small{ \ y \ }\)の増加量は小さいから、緩やかに増加していくけど増加することに変わりないから、\(\small{ \ y \ }\)はかなり大きい値にもなりうるからね。

これに対して\(\small{ \ x=\displaystyle\frac{1}{2}, \ \displaystyle\frac{1}{2^2}, \ \displaystyle\frac{1}{2^3},\cdots \ }\)と\(\small{ \ x \ }\)が小さくなると\(\small{ \ y=-1, \ -2, \ -3,\cdots \ }\)って\(\small{ \ y \ }\)も小さくなる。
\(\small{ \ x \ }\)の減少量に対して\(\small{ \ y \ }\)の減少量は大きいから、\(\small{ \ x \ }\)が\(\small{ \ 0 \ }\)に近づくと\(\small{ \ y \ }\)はかなり小さい値(\(\small{ \ -\infty \ }\))になるからね。
\(\small{ \ \log_ax \ }\)の真数\(\small{ \ x \ }\)は正の値だから、\(\small{ \ y=\log_ax \ }\)のグラフは\(\small{ \ x=0 \ }\)、つまり\(\small{ \ y \ }\)軸に限りなく近く。つまり\(\small{ \ y \ }\)軸が漸近線になるんだ。

次に底が\(\small{ \ 1 \ }\)より小さい\(\small{ \ y=\log_{\frac{1}{2}}x \ }\)のグラフを考えてみよう。
\(\small{ \ x=1, \ 2, \ 2^2, \ 2^3,\cdots \ }\)と\(\small{ \ x \ }\)が大きくなると\(\small{ \ y=0, \ -1, \ -2, \ -3,\cdots \ }\)って\(\small{ \ y \ }\)は小さくなるよね。
これに対して\(\small{ \ x=\displaystyle\frac{1}{2}, \ \displaystyle\frac{1}{2^2}, \ \displaystyle\frac{1}{2^3},\cdots \ }\)と\(\small{ \ x \ }\)が小さくなると\(\small{ \ y=1, \ 2, \ 3,\cdots \ }\)って\(\small{ \ y \ }\)は大きくなるんだ。
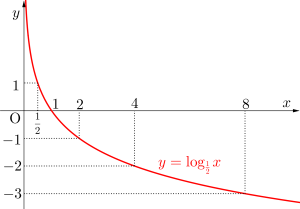
この場合も\(\small{ \ x \ }\)が小さくなるって言っても負の値になるわけじゃなくて、\(\small{ \ x=0 \ }\)に限りなく近づいていく。つまり\(\small{ \ y=\log_{\frac{1}{2}}x \ }\)のグラフは\(\small{ \ y=0 \ }\)つまり\(\small{ \ x \ }\)軸が漸近線になる。
ちなみに\(\small{ \ y=\log_2x \ }\)のグラフと\(\small{ \ y=\log_{\frac{1}{2}}x \ }\)のグラフは\(\small{ \ x \ }\)軸対称になっているからね。
まとめると\(\small{ \ y=\log_ax \ }\)は\(\small{ \ a\gt1 \ }\)ならグラフは単調増加、\(\small{ \ 0 \lt a \lt 1 \ }\)ならグラフは単調減少で、どちらのグラフも\(\small{ \ (1, \ 0) \ }\)を通って、\(\small{ \ x=0 \ }\)(\(\small{ \ y \ }\)軸)が漸近線になるんだ。

あと\(\small{ \ x \ }\)は常に正の値をとるから、定義域(\(\small{ \ x \ }\)の範囲)は\(\small{ \ x\gt0 \ }\)だけど、値域(\(\small{ \ y \ }\)の範囲)は実数全体になるから覚えておこう。
指数関数のグラフと対数関数のグラフ
次に指数関数と対数関数のグラフについて考えてみよう。
指数と対数の関係から\(\small{ \ y=\log_ax \ }\)は\(\small{ \ x=a^y \ }\)を満たすよね。
つまり\(\small{ \ y=\log_ax \ }\)と\(\small{ \ x=a^y \ }\)のグラフは同じグラフなんだ。

\(\small{ \ y=a^x \ }\)と\(\small{ \ x=a^y \ }\)は\(\small{ \ x \ }\)と\(\small{ \ y \ }\)を入れ替えた式だよね。
この\(\small{ \ x \ }\)と\(\small{ \ y \ }\)を入れ替えた式は\(\small{ \ y=x \ }\)について対称なグラフになるんだ。
だから\(\small{ \ y=a^x \ }\)と\(\small{ \ x=a^y \ }\)、つまり\(\small{ \ y=a^x \ }\)と\(\small{ \ y=\log_ax \ }\)は\(\small{ \ y=x \ }\)について対称なグラフになる。
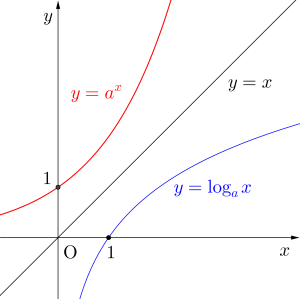
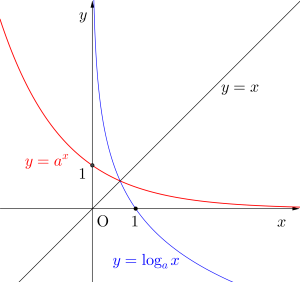
これは\(\small{ \ a \ }\)が\(\small{ \ 1 \ }\)より大きい場合でも小さい場合でも対称になるからね。
次に曲線上の点について考えてみよう。
\(\small{ \ y=\log_ax \ }\)上の点\(\small{ \ (p, \ q) \ }\)は\(\small{ \ q=\log_ap \ }\)を満たすよね。
\(\small{ \ y=x \ }\)について点\(\small{ \ (p, \ q) \ }\)に対称な点は\(\small{ \ y=a^x \ }\)上の点\(\small{ \ (q, \ p) \ }\)になるから\(\small{ \ p=a^q \ }\)を満たしていて、\(\small{ \ q=\log_ap \ }\)を代入すると\(\small{ \ p=a^{\log_ap} \ }\)になるんだ。
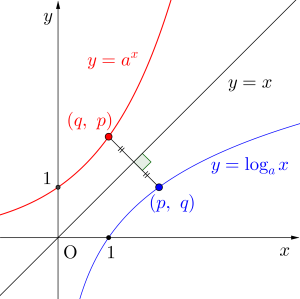
指数に対数が使われている場合、簡単に表示することができるから\(\small{ \ a^{\log_ap} \ }\)のような形を見たら指数の対数を消すことができるから必ず変形しよう。
対数関数のグラフの平行移動
グラフの平行移動は二次関数で勉強したときと同じで
\(\small{ \ x \ }\)軸方向に\(\small{ \ \alpha \ }\)平行移動するときは\(\small{ \ x \ }\)を\(\small{ \ x-\alpha \ }\)に、\(\small{ \ y \ }\)軸方向に\(\small{ \ \beta \ }\)平行移動するときは\(\small{ \ y \ }\)を\(\small{ \ y-\beta \ }\)に変えればよかったよね。
対数関数のグラフでもそれは同じだから、\(\small{ \ y=\log_2x \ }\)を\(\small{ \ x \ }\)軸方向に\(\small{ \ +2 \ }\)、\(\small{ \ y \ }\)軸方向に\(\small{ \ +4 \ }\)に移動したグラフは\(\small{ \ y-4=\log_2(x-2) \ }\)だから\(\small{ \ y=\log_2(x-2)+4 \ }\)になるからね。
対数関数のグラフと不等式
対数関数\(\small{ \ y=\log_ax \ }\)のグラフは\(\small{ \ a\gt1 \ }\)なら単調増加するグラフ、\(\small{ \ 0\lt a \lt1 \ }\)なら単調減少するグラフだったよね。不等式はこのグラフを利用して考えるんだ。
\(\small{ \ a\gt1 \ }\)のときグラフは単調増加だから
\(\small{ \ \log_aM\lt\log_aN \ }\)なら不等号の向きはそのまま\(\small{ \ M\lt N \ }\)
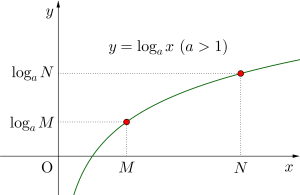
\(\small{ \ 0\lt a\lt 1 \ }\)のときグラフは単調減少だから
\(\small{ \ \log_aM\gt\log_aN \ }\)なら等号の向きが変わって\(\small{ \ M\lt N \ }\)
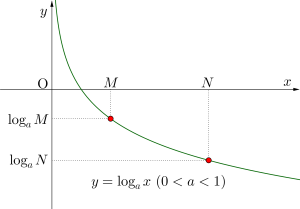
\(\small{ \ \log_ax \ }\)の底\(\small{ \ a \ }\)の大きさによって不等号の向きが変化するから注意しよう。\(\small{ \ \log_2x\lt \log_2y \ }\)のように底が数字の場合はいいけど、\(\small{ \ \log_ax\lt \log_ay \ }\)みたいに文字になっているときは\(\small{ \ a\gt1 \ }\)と\(\small{ \ 0\lt a \lt 1 \ }\)の場合分けが必要になるから注意しよう。
対数関数のグラフを利用した大小関係
指数関数には「次の数を小さい順に並べよ。」って問題がある。
この問題には\(\small{ \ \log_ap, \ \log_aq, \ \log_ar \ }\)を並べるものと、\(\small{ \ \log_pa, \ \log_qa, \ \log_ra \ }\)を並べるものの\(\small{ \ 2 \ }\)つのタイプがある。この\(\small{ \ 2 \ }\)つの問題はグラフで考えるようにしよう。
\(\small{ \ \log_pa, \ \log_qa, \ \log_ra \ }\)を比較する場合は\(\small{ \ y=\log_ax \ }\)のグラフから\(\small{ \ p, \ q, \ r \ }\)の大小を求めよう。
\(\small{ \ a\gt1 \ }\)と\(\small{ \ 0\lt a \lt 1 \ }\)で大小が変化するのも忘れないでね。
\(\small{ \ a\gt1 \ }\)のとき
\(\small{ \ p\lt q \lt r \ }\)なら\(\small{ \ \log_ap \lt \log_aq \lt \log_ar \ }\)
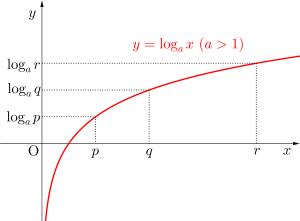
\(\small{ \ 0 \lt a\lt1 \ }\)のとき
\(\small{ \ p\lt q \lt r \ }\)なら\(\small{ \ \log_a^r \lt \log_aq \lt \log_ap \ }\)
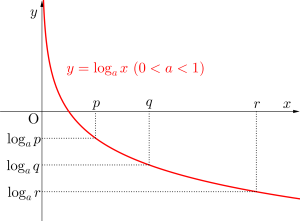
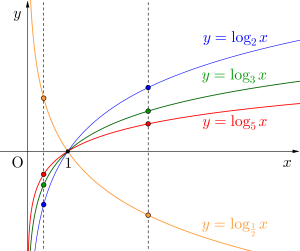
\(\small{ \ \log_pa, \ \log_qa, \ \log_ra \ }\)を比較する場合は\(\small{ \ y=\log_px, \ y=\log_qx, \ y=\log_rx \ }\)のグラフから大小を求めよう。
\(\small{ \ p\lt q \lt r \ }\)のとき
\(\small{ \ a\lt1 \ }\)なら\(\small{ \ \log_pa\lt \log_qa \lt \log_ra \ }\)
\(\small{ \ a\gt 1 \ }\)なら\(\small{ \ \log_ra\lt \log_qa \lt \log_pa \ }\)
\(\small{ \ a \ }\)が\(\small{ \ 1 \ }\)より大きいか小さいかによってグラフの大小が反転することに注意しよう。
っていっても定期試験ぐらいでしか出題されないような問題だけどね。でもどちらの問題でもきちんとグラフを考えて解けるようにしておこう。
次の数の大小を不等号を用いて表せ。
(1)\(\small{ \ \log_58, \ \log_{25}30, \ 2 \ }\)
(2)\(\small{ \ 0\lt x\lt a \lt1 \ }\)のとき
\(\small{ \ \log_ax, \ (\log_ax)^2, \ \log_a(\log_ax) \ }\)
(1)
\(\small{\begin{eqnarray} \ \log_{25}30&=&\displaystyle\frac{\log_530}{\log_525}\\
&=&\displaystyle\frac{\log_530}{2}\\
&=&\log_5\sqrt{30} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ 2&=&\log_55^2\\
&=&\log_525 \ \end{eqnarray}}\)
\(\small{ \ \sqrt{30}\lt8\lt25 \ }\)より
\(\small{ \ \log_{25}30\lt\log_58\lt 2 \ }\)
(2)
\(\small{ \ 0\lt x\lt a \lt1 \ }\)より
\(\small{ \ \log_ax\lt\log_aa=1 \ }\)
\(\small{ \ \log_ax\gt1 \ }\)より\(\small{ \ (\log_ax)^2\gt\log_ax \ }\)
\(\small{ \ \log_ax\gt1 \ }\)より\(\small{ \ \log_a(log_ax)\lt0 \ }\)
\(\small{ \ \therefore \log_a(\log_ax)\lt \log_ax \lt (\log_ax)^2 \ }\)

Point 対数関数のグラフとその利用
①\(\small{ \ y=\log_ax\ }\)は\(\small{ \ a\gt1 \ }\)と\(\small{ \ 0\lt a\lt1 \ }\)でグラフが異なる
②\(\small{ \ \log_ap\lt \log_aq \ }\)は\(\small{ \ a\gt1 \ }\)のとき\(\small{ \ p \lt q \ }\)、\(\small{ \ 0\lt a\lt1 \ }\)のとき\(\small{ \ p\gt q \ }\)

