こんにちは、リンス(@Lins016)です。
今回は対数関数の積分について学習していこう。
対数関数の積分
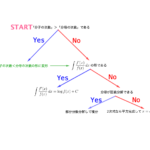
対数関数の積分って実はいろいろなパターンがあって、部分積分法のときもあれば、置換積分法のときもある。複数の解き方をまとめておいて、どの問題にも対応できるようにしておこう。
・部分積分法の利用
\(\small{ \ \displaystyle\int \ \log x \ dx=\displaystyle\int \ (x)'\log x \ dx \ }\)
・置換積分の利用
\(\small{ \ \displaystyle\int \ \displaystyle\frac{\log x}{x} \ dx=\displaystyle\int \ t \ dt \ }\)
対数関数の積分と部分積分法(1)
教科書では対数関数の積分は公式の扱いになっていなくて、部分積分法を利用して導くことになっている。
\(\small{\begin{eqnarray} \ \displaystyle\int \ \log x \ dx&=&\displaystyle\int \ (x)'\log x \ dx\\[3pt]
&=&x\log x-\displaystyle\int \ x\cdot\displaystyle\frac{1}{x} \ dx\\[3pt]
&=&x\log x-x+C \ \end{eqnarray}}\)
でもこれってよく出てくるものだから\(\small{ \ \displaystyle\int \ \log x \ dx=x\log x-x+C \ }\)って覚えていて欲しい。
これを覚えていれば\(\small{ \ \displaystyle\int \ \log (x+3) \ dx \ }\)も簡単に解ける。
\(\small{ \ \displaystyle\int \ \log x \ dx=x\log x-x+C \ }\)だから
展開した定数部分は\(\small{ \ C-3 \ }\)になるけど、これは積分定数としてまとめてもいいから
って書けるからね。
実際は
って解くんだけどね。
でも\(\small{ \ \displaystyle\int \ \log x \ dx=x\log x-x+C \ }\)覚えてたら簡単でしょ。実際学校の定期試験だときちんと解かないと減点されるかもしれないけど、入試のこと考えるとそれぐらい覚えておこうって思う。
ただ注意しないといけないのは次の場合。
\(\small{ \ \displaystyle\int \ \log (2x+1) \ dx \ }\)について考えてみよう。
\(\small{ \ \displaystyle\int \ \log x \ dx=x\log x-x+C \ }\)だから
になるのかな。
計算してみると
だから
にならなかったよね。
\(\small{ \ \displaystyle\int \ \log (x+3) \ dx \ }\)はうまくいったのに\(\small{ \ \displaystyle\int \ \log (2x+1) \ dx \ }\)はうまくいかない。
これは置換積分してみるとわかる。
\(\small{ \ t=x+3 \ }\)とすると\(\small{ \ \displaystyle\frac{dt}{dx}=1 \ }\)だから
\(\small{ \ \displaystyle\int \ \log (x+3) \ dx= \displaystyle\int \ \log t \ dt \ }\)になる。
でも\(\small{ \ t=2x+1 \ }\)とすると\(\small{ \ \displaystyle\frac{dt}{dx}=2 \ }\)になるから
\(\small{ \ \displaystyle\int \ \log (2x+1) \ dx= \displaystyle\int \ \displaystyle\frac{1}{2}\log t \ dt \ }\)になる。
当然\(\small{ \ \displaystyle\int \ \log t \ dx=t\log t-t+C \ }\)だから、どっちの式も元に戻すと
\(\small{ \ \displaystyle\int \ \log (2x+1) \ dx=\displaystyle\frac{1}{2}(2x+1)\log (2x+1)-\displaystyle\frac{1}{2}(2x+1)+C \ }\)
定数部分をまとめて\(\small{ \ C \ }\)と書くことにすると
\(\small{ \ \displaystyle\int \ \log (2x+1) \ dx=\displaystyle\frac{1}{2}(2x+1)\log (2x+1)-x+C \ }\)
ってなるんだ。
つまり「\(\small{ \ t=x \ }\)の\(\small{ \ 1 \ }\)次式」っておいたとき、\(\small{ \ \displaystyle\frac{dt}{dt} \ }\)の値を考えて答えよう。
一般化すると
つまり
\(\small{ \ \displaystyle\int(ax+b) \ dx=\displaystyle\frac{1}{a}(ax+b)\log (ax+b)-x+C \ }\)
になる。
\(\small{ \ \displaystyle\int \ \log}\)(\(\small{ x \ }\)の\(\small{ \ 1 \ }\)次式)\(\small{ \ dx \ }\)は部分積分を利用したこの形になるからね。
対数関数の積分と部分積分法(2)
次に部分積分法を使う他の形について考えてみよう。
\(\small{ \ \displaystyle\int \ x^n \log x \ dx \ }\)(ただし\(\small{ \ n\neq1 \ }\))
この形は部分積分法を利用して解こう。
例えば
他にも
\(\small{\begin{eqnarray} \ \displaystyle\int \ \sqrt{x} \log x &=&\displaystyle\int x^{\textstyle\frac{1}{2}}\log x \ dx \\[3pt]
&=&\displaystyle\int\left(\displaystyle\frac{2}{3}x^{\textstyle\frac{3}{2}}\right)' \log x \ dx \\[3pt]
&=&\displaystyle\frac{2}{3}x^{\textstyle\frac{3}{2}} \log x- \displaystyle\int \ \displaystyle\frac{2}{3}x^{\textstyle\frac{3}{2}} \cdot \displaystyle\frac{1}{x} \ dx\\[3pt]
&=&\displaystyle\frac{2}{3}x\sqrt{x} \log x- \displaystyle\frac{4}{9}x\sqrt{x}+C \ \end{eqnarray}}\)
ただ\(\small{ \ n=-1 \ }\)のとき、つまり\(\small{ \ \displaystyle\int \ \displaystyle\frac{\log x}{x} \ dx \ }\)は違う解き方になるから注意しよう。
対数関数の積分と部分積分法(3)
さらに対数の真数が\(\small{ \ x \ }\)の\(\small{ \ 2 \ }\)次式の場合について考えてみよう。
\(\small{ \ \displaystyle\int \ x \log (x^2+1) \ dx \ }\)について考えてみよう。
この場合も部分積分法を使う。部分積分の公式は
だったよね。
特に対数関数を含む部分積分は対数関数を\(\small{ \ f(x) \ }\)にするんだったよね。
-

部分積分法とそのやり方
部分積分を利用する形やパターン分けについて詳しく解説しています。
続きを見る
だから\(\small{ \ \displaystyle\int \ x \log (x^2+1) \ dx \ }\)も\(\small{ \ f(x)= \log (x^2+1) \ }\)として解こう。
対数関数を含む部分積分法を利用した計算は、対数関数を\(\small{ \ f(x) \ }\)として計算しよう。

-

分数関数の積分
分数関数の形による解き方について詳しく解説しています。
続きを見る
対数関数と置換積分
最後に置換積分を利用する対数関数の積分について考えてみよう。
\(\small{ \ t= \log x \ }\)とおくと\(\small{ \ \displaystyle\frac{dt}{dx}=\displaystyle\frac{1}{x} \ }\)だから\(\small{ \ \displaystyle\int \ \displaystyle\frac{\log x}{x} \ dx \ }\)は\(\small{ \ \displaystyle\int \ t \ dt \ }\)に変わるよね。
置換積分を利用する他の問題も見てみよう。
\(\small{ \ \displaystyle\int \ \displaystyle\frac{(\log x)^2}{x} \ dx \ }\)なら\(\small{ \ t= \log x \ }\)とおいて\(\small{ \ \displaystyle\frac{dt}{dx}=\displaystyle\frac{1}{x} \ }\)
\(\small{\begin{eqnarray}\displaystyle\int \ \displaystyle\frac{(\log x)^2}{x} \ dx&=&\displaystyle\int \ t^2 \ dt\\[3pt]
&=&\displaystyle\frac{1}{3}t^3+C\\[3pt]
&=&\displaystyle\frac{1}{3}\left(\log x\right)^3+C \ \end{eqnarray}}\)
になるよね。
\(\small{ \ \log x \ }\)と\(\small{ \ \displaystyle\frac{1}{x} \ }\)がある積分は置換積分を利用しよう。
次の不定積分を求めよ。
(1)\(\small{ \ \displaystyle\int \ \log (x^2-1) \ dx \ }\)
(2)\(\small{ \ \displaystyle\int \ \displaystyle\frac{\log x}{x(\log x+1)^2} \ dx \ }\)
(1)
(2)
\(\small{ \ \displaystyle\int \ \displaystyle\frac{\log x}{x(\log x+1)^2} \ dx \ }\)
\(\small{ \ t= \log x+1 \ }\)とおく
\(\small{ \ \displaystyle\frac{dt}{dx}= \displaystyle\frac{1}{x} \ }\)
Point 対数関数の積分
①対数関数の形によってどの積分を利用するか考える
②積分の解法は確実にマスターする