区分求積法とその解き方

こんにちは、リンス(@Lins016)です。
今回は区分求積法とその解き方について学習していこう。

定積分と和の極限

このあと学習するんだけど、\(\small{ \ \displaystyle \int_{a}^{ b } f(x) dx \ }\)で\(\small{ \ x \ }\)軸と\(\small{ \ y=f(x) \ }\)と\(\small{ \ x=a, \ x=b \ }\)で囲まれた面積（\(\small{ \ f(x)\geqq0 \ }\)のとき）を求めることが出来るんだ。

今回はなぜこの式で面積を求めることが出来るのか、よく試験に出される問題を解きながら、区分求積法を理解していこう。

区分求積法とは

区分求積法とは名前が表している通りで面積を区分して求める方法のことなんだ。

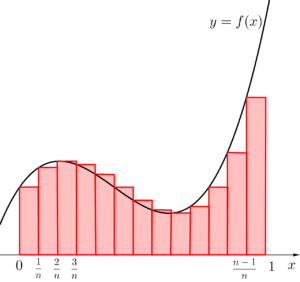
\(\small{ \ y=x^2 \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=1 \ }\)で囲まれた面積について考えてみよう。まずは区間\(\small{ \ [0, \ 1] \ }\)を\(\small{ \ n \ }\)等分して、\(\small{ \ n \ }\)個の長方形を作る。これらの長方形の面積の和を\(\small{ \ \mathrm{S}_n \ }\)とすると、

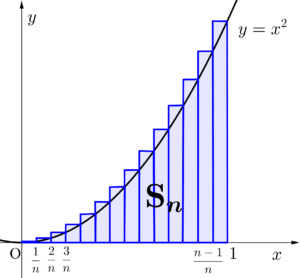
どの長方形も横幅は\(\small{ \ \displaystyle\frac{1}{n} \ }\)になるから

になる。

この数列の和は初項に\(\small{ \ n \ }\)を含む数列の和だから\(\small{ \ k \ }\)項目を考えて\(\small{ \ \displaystyle \sum_{k=1}^n a_k \ }\)を考えれば良かったよね。

だから

になる。

このときこの面積って\(\small{ \ y=x^2 \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=1 \ }\)で囲まれた面積より少し大きいよね。

下の図を見てもらうとわかるけど、区間\(\small{ \ [0, \ 1] \ }\)を分割する長方形の数が増えると、\(\small{ \ y=x^2 \ }\)より上にはみ出している部分が小さくなっていくのがわかるよね。

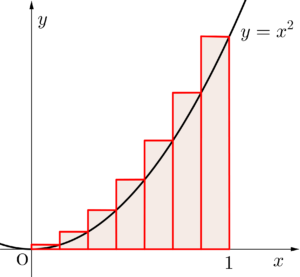
つまり\(\small{ \ n\to \infty \ }\)にすれば、\(\small{ \ \mathrm{S}_n \ }\)は\(\small{ \ y=x^2 \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=1 \ }\)で囲まれた面積\(\small{ \ \mathrm{S} \ }\)に限りなく近くことがわかる。

\(\small{ \ y=x^2 \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=1 \ }\)で囲まれた面積を\(\small{ \ \mathrm{S} \ }\)とすると、\(\small{ \ \displaystyle \lim_{ n \to \infty } \mathrm{S}_n = \mathrm{S} \ }\)が成り立つんだ。

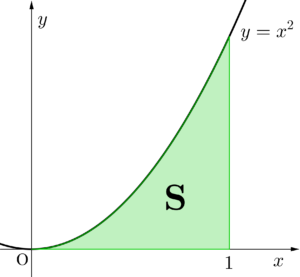
ちなみに
\(\small{ \ \mathrm{S}=\displaystyle\int_0^1 x^2 dx= \left[ \displaystyle\frac{x^3}{3} \right]_0^1= \displaystyle\frac{1}{3}\ }\)
\(\small{\begin{eqnarray} \ \displaystyle \lim_{ n \to \infty }\mathrm{S}_n&=&\displaystyle \lim_{ n \to \infty }\displaystyle\frac{1}{n^3}\cdot \displaystyle\frac{1}{6}n(n+1)(2n+1)\\
&=&\displaystyle \lim_{ n \to \infty }\displaystyle\frac{1}{6}\left(1+\displaystyle\frac{1}{n}\right)\left(2+\displaystyle\frac{1}{n}\right)\\
&=&\displaystyle\frac{1}{3} \ \end{eqnarray}}\)
になるから\(\small{ \ \displaystyle \lim_{ n \to \infty } \mathrm{S}_n = \mathrm{S} \ }\)が成り立つことが計算で確かめられたよね。

区分求積法の考え方

次にこれを一般化してみよう。
まずは、\(\small{ \ y=f(x)\geqq0 \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=0 \ }\)、\(\small{ \ x=1 \ }\)で囲まれた面積\(\small{ \ \mathrm{S} \ }\)を考えるために、区間\(\small{ \ [0, \ 1] \ }\)を\(\small{ \ n \ }\)等分して、\(\small{ \ n \ }\)個の長方形を作る。

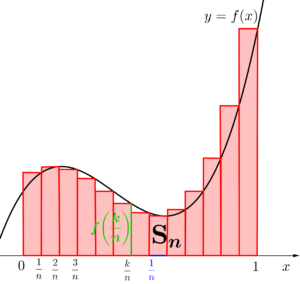
長方形の面積の和\(\small{ \ \mathrm{S}_n \ }\)は

\(\small{\begin{eqnarray} \ \mathrm{S}_n&=&\displaystyle\frac{1}{n}f\left(\textstyle\frac{1}{n}\right)+\displaystyle\frac{1}{n}f\left(\textstyle\frac{2}{n}\right)+\displaystyle\frac{1}{n}f\left(\textstyle\frac{3}{n}\right)+\cdots+\displaystyle\frac{1}{n}f\left(\textstyle\frac{n}{n}\right)\\
&=&\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n f\left(\textstyle\frac{k}{n}\right) \ \end{eqnarray}}\)

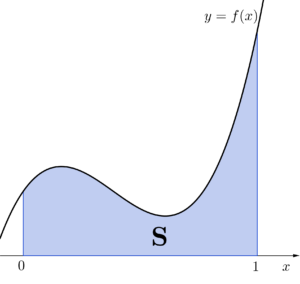
　　\(\small{ \ \mathrm{S}=\displaystyle\int_0^1f(x)dx \ }\)

さっきと同じで\(\small{ \ n\to \infty \ }\)にすると、\(\small{ \ \mathrm{S}_n \ }\)は\(\small{ \ \mathrm{S} \ }\)に限りなく近くことから、\(\small{ \ \displaystyle \lim_{ n \to \infty } \mathrm{S}_n = \mathrm{S} \ }\)になるんだ。

これから\(\small{ \ \displaystyle \lim_{ n \to \infty }\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n f\left(\textstyle\frac{k}{n}\right)=\int_0^1 f(x) dx \ }\)が言えるんだ。

この形が一番試験には出やすいから、しっかりと覚えておこう。数列の極限の問題だって思ってると答えが出せないってことになるからね。

それと\(\small{ \ f(x)\geqq0 \ }\)だったけど、\(\small{ \ f(x)\leqq0 \ }\)でも成り立つからね。

区分求積法と定積分

さらに\(\small{ \ y=f(x)\geqq0 \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=a \ }\)、\(\small{ \ x=b \ }\)で囲まれた面積\(\small{ \ \mathrm{S} \ }\)を考えるために、区間\(\small{ \ [a, \ b] \ }\)を\(\small{ \ n \ }\)等分して、\(\small{ \ n \ }\)個の長方形を作る。
\(\small{ \ a \ }\)から\(\small{ \ b \ }\)までを\(\small{ \ n \ }\)等分するので、その一つの長方形の横幅は\(\small{ \ \Delta x=\displaystyle\frac{b-a}{n} \ }\)になる。

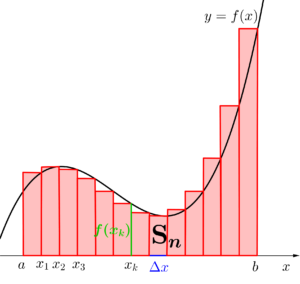
だから長方形の面積の和\(\small{ \ \mathrm{S}_n \ }\)は
\(\small{\begin{eqnarray} \ \mathrm{S}_n&=&f\left(x_1\right)\Delta x+f\left(x_2\right)\Delta x+f\left(x_3\right)\Delta x+\cdots+f\left(x_n\right)\Delta x\\
&=&\displaystyle\sum_{k=1}^n f\left(x_k\right)\Delta x \ \end{eqnarray}}\)

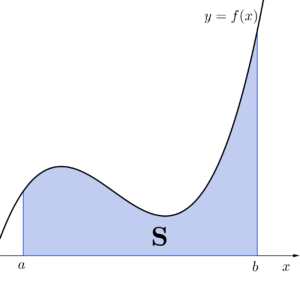
　　\(\small{ \ \mathrm{S}=\displaystyle\int_a^b f(x) dx \ }\)

当然これも\(\small{ \ n\to \infty \ }\)にすると、\(\small{ \ \mathrm{S}_n \ }\)は\(\small{ \ \mathrm{S} \ }\)に限りなく近くことから、\(\small{ \ \displaystyle \lim_{ n \to \infty }\mathrm{S}_n=\mathrm{S} \ }\)になる。
\(\small{ \ \displaystyle \lim_{ n \to \infty }\displaystyle\sum_{k=1}^n f\left(x_k\right)\Delta x=\displaystyle\int_a^bf(x)dx \ }\)、\(\small{ \ \Delta x =\displaystyle\frac{b-a}{n}, \ x_k=a+k\Delta x \ }\)

この式に\(\small{ \ a=0, \ b=1 \ }\)を代入すると\(\small{ \ \displaystyle \lim_{ n \to \infty }\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n f\left(\textstyle\frac{k}{n}\right)=\displaystyle\int_a^bf(x)dx \ }\)ってなるんだ。

区分求積法の解き方

一番重要なのはここからだよね。区分求積法について理解できても、問題の答えが出せないと意味ないからね。区分求積法の問題を解く上で大切なのは二つある。

一つ目は問題が区分求積法の問題だって気付くこと。
単純に見ると数列の和の極限（無限級数）に見えるから、数列の和の極限だと思って解くと大変だからね。

二つ目は数列の和の極限（無限級数）から\(\small{ \ f(x) \ }\)を求めること。
結局\(\small{ \ f(x) \ }\)が求められないと答えが出ないからね。

特に出題されるのは\(\small{ \ y=f(x) \ }\)と\(\small{ \ x \ }\)軸、\(\small{ \ x=0 \ }\)、\(\small{ \ x=1 \ }\)で囲まれた面積の形だから、この形を確実にできるようにしよう。

それじゃ問題を考えてみよう。
\(\small{ \ \displaystyle\lim_{n\to \infty}\left(\displaystyle\frac{1}{n+1}+\displaystyle\frac{1}{n+2}+\displaystyle\frac{1}{n+3}+\cdots+\displaystyle\frac{1}{n+n}\right) \ }\)を解きながら、区分求積法の解き方を確実におさえていこう。

無限級数の問題を解くとき、\(\small{ \ n \ }\)項目までの部分和を出す必要があるよね。（必ずじゃないけど、出すことの方が多い。）
和を求めるには、まずは一般項を求めるってのが基本だよね。しかもこの区分求積法を利用する無限級数の和は初項に\(\small{ \ n \ }\)が入っている数列の和になるから、まずは第\(\small{ \ k \ }\)項を求めよう。

数列の和の極限（無限級数）から\(\small{ \ f(x) \ }\)を求めるために、まずは\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\sum_{k=1}^na_k \ }\)の形に変形する必要があるんだ。

この数列の第\(\small{ \ k \ }\)項目を\(\small{ \ a_k \ }\)とすると\(\small{ \ a_k=\displaystyle\frac{1}{n+k} \ }\)になる。
つまり\(\small{ \ \displaystyle\sum \ }\)を利用すると

になる。

この時点での部分和を求めることができるなら数列の極限の問題ってことになるけど、部分和が\(\small{ \ n \ }\)の式で表すことができない形だったら、区分求積法を利用するんじゃないかって考えよう。

区分求積法の長方形は横幅\(\small{ \ \displaystyle\frac{1}{n} \ }\)×縦幅の形が基本だから、横幅の\(\small{ \ \displaystyle\frac{1}{n} \ }\)が必要なんだ。

だから第\(\small{ \ k \ }\)項を無理矢理\(\small{ \ \displaystyle\frac{1}{n} \ }\)との積の形にすると\(\small{ \ \displaystyle\frac{1}{n+k}=\displaystyle\frac{1}{n}\times\displaystyle\frac{n}{n+k} \ }\)
つまり

\(\small{ \ \displaystyle\frac{1}{n} \ }\)は\(\small{ \ k \ }\)がないから\(\small{ \ \displaystyle\sum \ }\)の前に出すことができるよね。式変形はまずはここまでが第一段階なんだ。

次に\(\small{ \ \displaystyle\frac{1}{n} \ }\)を前に出した後の\(\small{ \ \displaystyle\sum \ }\)の後ろにある\(\small{ \ \displaystyle\frac{n}{n+k} \ }\)から\(\small{ \ f(x) \ }\)を求めるんだけど、基本の形をまずチェックしておこう。
\(\small{ \ \displaystyle\lim_{ n \to \infty } \displaystyle\frac{1}{n}\displaystyle \sum_{k=1}^n f\left(\textstyle\frac{k}{n}\right)= \displaystyle \int_{0}^{1} f(x) dx \ }\)が基本だから、\(\small{ \ \displaystyle\sum \ }\)の後ろを\(\small{ \ \displaystyle\frac{k}{n}=x \ }\)ってしたい。
だから次は無理矢理\(\small{ \ \displaystyle\frac{k}{n} \ }\)を作る必要があるんだ。

とにかく元の式が変形しないように\(\small{ \ k \ }\)を\(\small{ \ \displaystyle\frac{k}{n} \ }\)に変える必要がある。元の式が変形されると違う式になるからね。

だから分母分子ともに\(\small{ \ n \ }\)で割ればいい。
\(\small{ \ \displaystyle\frac{n}{n+k}=\displaystyle\frac{1}{1+\textstyle\frac{k}{n}} \ }\)
つまり\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\displaystyle\frac{n}{n+k}=\displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\displaystyle\frac{1}{1+\textstyle\frac{k}{n}} \ }\)

\(\small{ \ \displaystyle\lim_{ n \to \infty } \displaystyle\frac{1}{n}\displaystyle \sum_{k=1}^n f\left(\textstyle\frac{k}{n}\right)= \displaystyle \int_{0}^{1} f(x) dx \ }\)で\(\small{ \ \displaystyle\sum \ }\)の後ろの部分を\(\small{ \ \displaystyle\frac{k}{n}=x \ }\)に変えて積分すればいいから、
\(\small{\begin{eqnarray} \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\displaystyle\frac{1}{1+\textstyle\frac{k}{n}}&=&\displaystyle\int_0^1\displaystyle\frac{1}{1+x}dx\\
&=&\left[\log (1+x)\right]_0^1\\
&=&\log 2 \ \end{eqnarray}}\)

\(\small{ \ \displaystyle\sum \ }\)の前に\(\small{ \ \displaystyle\frac{1}{n} \ }\)を括りだして、\(\small{ \ \displaystyle\sum \ }\)の後ろに\(\small{ \ \displaystyle\frac{k}{n} \ }\)を作る。この\(\small{ \ \displaystyle\frac{k}{n} \ }\)を作ったとき\(\small{ \ \displaystyle\sum \ }\)の後ろに\(\small{ \ \displaystyle\frac{k}{n} \ }\)以外に\(\small{ \ n \ }\)や\(\small{ \ k \ }\)が残っていたらダメなんだ。\(\small{ \ \displaystyle\frac{k}{n} \ }\)は\(\small{ \ x \ }\)に変えられるけど、\(\small{ \ n \ }\)や\(\small{ \ k \ }\)はなんて変えたらいいかわからないからね。

もう一つの区分求積法

あと注意しておきたい問題がある。
例えば次の問題を見てみよう。

これをさっきと同じように考えると
(与式)
\(\small{\begin{eqnarray}&=&\displaystyle\lim_{n\to \infty}\displaystyle\sum_{k=1}^n\displaystyle\frac{n^2}{(n+k-1)^3}\\
&=&\displaystyle\lim_{n\to \infty}\displaystyle\sum_{k=1}^n\displaystyle\frac{1}{n}\cdot\displaystyle\frac{n^3}{(n+k-1)^3}\\
&=&\displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\left(\displaystyle\frac{n}{n+k-1}\right)^3\\
&=&\displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\left(\displaystyle\frac{1}{1+\textstyle\frac{k}{n}-\textstyle\frac{1}{n}}\right)^3 \ \end{eqnarray}}\)
\(\small{ \ \displaystyle\frac{k}{n}=x \ }\)にしても\(\small{ \ \displaystyle\frac{1}{n} \ }\)が残ってるよね。

\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\left(\displaystyle\frac{1}{1+\textstyle\frac{k}{n}}\right)^3 \ }\)なら\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^n\left(\displaystyle\frac{1}{1+\textstyle\frac{k}{n}}\right)^3=\displaystyle\int_0^1\left(\displaystyle\frac{1}{1+x}\right)^3 dx \ }\)って変形できるけど、この問題だと\(\small{ \ \displaystyle\frac{k}{n}=x \ }\)っておいても\(\small{ \ \displaystyle\frac{1}{n} \ }\)をどうすればいいかわからないよね。

\(\small{ \ \displaystyle\frac{1}{n} \ }\)が余ってしまう時は「\(\small{ \ k=1 \ }\)から\(\small{ \ k=n \ }\)までの和」を「\(\small{ \ k=0 \ }\)から\(\small{ \ k=n-1 \ }\)までの和」として考えてみよう。
\(\small{ \ \displaystyle\sum_{k=1}^n\left(\displaystyle\frac{1}{1+\textstyle\frac{k}{n}-\textstyle\frac{1}{n}}\right)^3=\displaystyle\sum_{k=0}^{n-1}\left(\displaystyle\frac{1}{1+\textstyle\frac{k}{n}}\right)^3 \ }\)
こう変形することで\(\small{ \ \displaystyle\frac{1}{n} \ }\)を消すことができる。

でもこの変形って確かにあってるけど、これで極限とったら同じ面積になるのかなって思うよね。これって実は次の長方形の面積の和を表すことになるんだ。

\(\small{ \ k=1 \ }\)から\(\small{ \ k=n \ }\)までの和

\(\small{ \ \displaystyle\frac{1}{n}\left\{f\left(\textstyle\frac{1}{n}\right)+f\left(\textstyle\frac{2}{n}\right)+f\left(\textstyle\frac{3}{n}\right)+\cdots+f\left(\textstyle\frac{n}{n}\right)\right\} \ }\)

\(\small{ \ k=0 \ }\)から\(\small{ \ k=n-1 \ }\)までの和

\(\small{ \ \displaystyle\frac{1}{n}\left\{f\left(0\right)+f\left(\textstyle\frac{1}{n}\right)+f\left(\textstyle\frac{2}{n}\right)+\cdots+f\left(\textstyle\frac{n-1}{n}\right)\right\} \ }\)

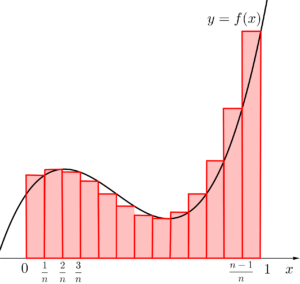
たしかに上の二つの図だと長方形の面積は全然違うけど、\(\small{ \ n\to\infty \ }\)にするとどちらの長方形の面積も\(\small{ \ \displaystyle\int_{0}^{1}f(x)dx \ }\)に近づくのがわかるよね。

だから\(\small{ \ \displaystyle\frac{1}{n} \ }\)が余ってしまう時は「\(\small{ \ k=1 \ }\)から\(\small{ \ k=n \ }\)までの和」を「\(\small{ \ k=0 \ }\)から\(\small{ \ k=n-1 \ }\)までの和」として考えてみよう。

とにかく第\(\small{ \ k \ }\)項目を求めて、和の形から\(\small{ \ f(x) \ }\)を求められるようにしよう。

Point 区分求積法とその解き方

①区分求積法の問題って見極める
②和記号から\(\small{ \ \displaystyle\frac{1}{n} \ }\)で括りだす
③\(\small{ \ \displaystyle\frac{k}{n} \ }\)を作って\(\small{ \ x \ }\)とおいて\(\small{ \ f(x) \ }\)を求める