こんにちは、リンス(@Lins016)です。
今回は余事象の利用について学習していこう。
余事象の便利さ
確率の基本性質で余事象を利用する場合、「少なくとも〜」って問題文に書いてあったら余事象を利用しようって話したけど、今回は余事象の便利さについて学習してみよう。
確率の問題を解く上で絶対に覚えてほしいテクニックの一つだからね。
「少なくとも」と余事象
余事象をいつ使えばいいのか?っていうと色々な場面があるけど、確実に注目したい文字に「少なくとも」って言葉がある。この言葉が問題文に書いてあったら余事象を考えるって思ってていい。
まずは簡単な問題で確認してみよう。
問題
コインを\(\small{ \ 5 \ }\)回投げて少なくとも\(\small{ \ 2 \ }\)回は表が出る確率を求めよ。
求める確率は「表が\(\small{ \ 2 \ }\)回裏が\(\small{ \ 3 \ }\)回出る確率」、「表が\(\small{ \ 3 \ }\)回裏が\(\small{ \ 2 \ }\)回出る確率」、「表が\(\small{ \ 4 \ }\)回裏が\(\small{ \ 1 \ }\)回出る確率」、「表が\(\small{ \ 5 \ }\)回裏が\(\small{ \ 0 \ }\)回出る確率」の\(\small{ \ 4 \ }\)つの場合で、これらは排反だから確率の和が答えになるよね。今回は答えの値を求めるんじゃなくて、この答えを出す手順について考えていこう。
表が\(\small{ \ k \ }\)回裏が\(\small{ \ 5-k \ }\)回出る確率を\(\small{ \ p_k \ }\)ってすると、求める確率は\(\small{ \ p_2+p_3+p_4+p_5 \ }\)になるよね。
確率\(\small{ \ p_k \ }\)は\(\small{ \ 5 \ }\)回中表が\(\small{ \ k \ }\)回裏が\(\small{ \ 5-k \ }\)回出る確率だから、反復試行の確率で、\(\small{ \ p_k={}_n\mathrm{C}_k \left(\displaystyle\frac{1}{2}\right)^k\left(\displaystyle\frac{1}{2}\right)^{5-k} \ }\)になるよね。
だからこの式に\(\small{ \ k=2 \ }\)から\(\small{ \ k=5 \ }\)まで代入して足せば答えは出る。でもそれだと計算が大変だよね。
少しでも計算が楽な方法で解きたいよね。だから別な方法で考えてみよう。
全ての確率の和は\(\small{ \ 1 \ }\)になるから、\(\small{ \ p_0+p_1+p_2+p_3+p_4+p_5=1 \ }\)が言える。
つまり、\(\small{ \ p_2+p_3+p_4+p_5 \ }\)を求めるよりも、\(\small{ \ p_0+p_1 \ }\)を求めた方が簡単だよね。これが余事象を利用した求め方になるんだ。
答えを直接求めるんじゃなくて、答えじゃない確率を求めてそれを全体(\(\small{ \ 1 \ }\))から引けばいいって考え方だよね。こういう問題って割と多いから「少なくとも」って言葉を見たら余事象を利用しようって考えてほしい。
ちなみに、\(\small{ \ p_k \ }\)の式が立てられなかった人は以前の記事で復習しておこう。確率では反復試行の確率の式って確実におさえておきたい式になるからね。
-

反復試行の確率
2つの事象の反復試行の確率や3つの事象の反復試行の確率について詳しく解説しています。
続きを見る
受験生だったら
\(\small{ \ p_0+p_1+p_2+p_3+p_4+p_5=1 \ }\)
\(\small{ \ \displaystyle\sum_{k=0}^{5}p_k=\displaystyle\sum_{k=0}^{5}{}_n\mathrm{C}_k \left(\displaystyle\frac{1}{2}\right)^k\left(\displaystyle\frac{1}{2}\right)^{5-k} \ }\)
で二項定理まで合わせてチェックしておこう。
-

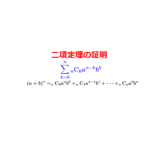
二項定理の証明
数学的帰納法を用いた二項定理の証明について詳しく解説しています。
続きを見る
少なくともがない問題と余事象
もちろん「少なくとも」って書いてない問題でも余事象を利用した方が簡単な問題はある。次の問題だとどうかな。
問題
\(\small{ \ 5 \ }\)回に\(\small{ \ 1 \ }\)回の割合で帽子を忘れるくせのある\(\small{ \ \mathrm{K} \ }\)君が、\(\small{ \ \mathrm{A} \ }\)、\(\small{ \ \mathrm{B} \ }\)、\(\small{ \ \mathrm{C} \ }\)を順に回って家に帰ったとき、どこかの家に帽子を忘れてきた確率を求めよ。
帽子を忘れてくる確率は「\(\small{ \ \mathrm{A} \ }\)で忘れる確率」、「\(\small{ \ \mathrm{B} \ }\)で忘れる確率」、「\(\small{ \ \mathrm{C} \ }\)で忘れる確率」の\(\small{ \ 3 \ }\)通りあるから、計算すると
\(\small{ \ \displaystyle\frac{1}{5}+ \displaystyle\frac{4}{5}\times\displaystyle\frac{1}{5}+\displaystyle\frac{4}{5}\times \displaystyle\frac{4}{5}\times\displaystyle\frac{1}{5}= \displaystyle\frac{61}{125} \ }\)
になる。
でもこれを余事象を利用して考えると、どこにも忘れない確率を求めればいいから、どこにも忘れない確率は
\(\small{ \ \left(\displaystyle\frac{4}{5}\right)^3=\displaystyle\frac{64}{125} \ }\)
だからどこかに忘れる確率は\(\small{ \ 1-\displaystyle\frac{64}{125}=\displaystyle\frac{61}{125} \ }\)になる。
この問題みたいに、「少なくとも」って言葉がなくても余事象を利用できる問題もあるから注意しよう。
余事象を利用しない計算
さっきの問題だと余事象を利用しなくても、特に解けないってこともなかったよね。計算量もそこまで違いがなかったし。それじゃ次はもう少し難易度の高い問題で余事象を利用する解き方と利用しない解き方ではどれくらい計算量が変わるの確認してみよう。
ただ、この問題の余事象を利用しない計算には数列の和の計算が必要だから、まだ数列を習っていない人はこれ以降は読まなくても大丈夫。受験生や数列を既に教わっている人は最後まで読んでおこう。
問題
\(\small{ \ 9 \ }\)枚のカードに\(\small{ \ 1 \ }\)から\(\small{ \ 9 \ }\)までの数字が\(\small{ \ 1 \ }\)つずつ記してある。このカードの中から任意に\(\small{ \ 1 \ }\)枚を抜き出し、その数字を記録し、もとのカードの中に戻すという操作を\(\small{ \ n \ }\)回繰り返す。このとき記録された数の積が\(\small{ \ 10 \ }\)で割り切れる確率を求めよ。
問題文には「少なくとも」って書いてないけど、\(\small{ \ 10 \ }\)で割り切れるってことは「偶数と\(\small{ \ 5 \ }\)が少なくとも\(\small{ \ 1 \ }\)回は出る」ってことだよね。
まずは余事象を利用して解いてみよう。
余事象の利用
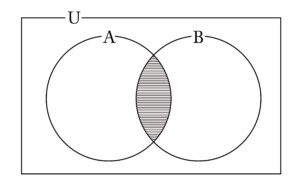
少なくとも偶数が\(\small{ \ 1 \ }\)回出る事象を\(\small{ \ \mathrm{A} \ }\)、少なくとも\(\small{ \ 5 \ }\)が\(\small{ \ 1 \ }\)回出る事象を\(\small{ \ \mathrm{B} \ }\)とすると、
求める確率は\(\small{ \ P\left(\mathrm{A\cap B}\right) \ }\)になる。
この余事象を考えると
P\left(\overline{\mathrm{A\cap B}}\right)=P\left(\overline{\mathrm{A}}\cup\overline{\mathrm{B}}\right)=P\left(\overline{\mathrm{A}}\right)+P\left(\overline{\mathrm{B}}\right)-P\left(\overline{\mathrm{A}}\cap\overline{\mathrm{B}}\right)}\)
ここで\(\small{ \ P\left(\overline{\mathrm{A}}\right) \ }\)は奇数しか出ない確率だから
\(\small{ \ P\left(\overline{\mathrm{A}}\right)=\left(\displaystyle\frac{5}{9}\right)^n \ }\)
\(\small{ \ P\left(\overline{\mathrm{B}}\right) \ }\)は\(\small{ \ 5 \ }\)が出ない確率だから
\(\small{ \ P\left(\overline{\mathrm{B}}\right)=\left(\displaystyle\frac{8}{9}\right)^n \ }\)
\(\small{ \ P\left(\overline{\mathrm{A}}\cap\overline{\mathrm{B}}\right) \ }\)は奇数かつ\(\small{ \ 5 \ }\)が出ない確率、つまり\(\small{ \ 1, \ 3, \ 7, \ 9 \ }\)しか出ない確率だから
\(\small{ \ P\left(\overline{\mathrm{A}}\cap\overline{\mathrm{B}}\right)=\left(\displaystyle\frac{4}{9}\right)^n \ }\)
したがって
\(\small{
\begin{eqnarray}
P\left(\overline{\mathrm{A\cap B}}\right)&=&P\left(\overline{\mathrm{A}}\cup\overline{\mathrm{B}}\right)\\[3pt]
&=&P\left(\overline{\mathrm{A}}\right)+P\left(\overline{\mathrm{B}}\right)-P\left(\overline{\mathrm{A}}\cap\overline{\mathrm{B}}\right)\\[3pt]
&=&\left(\displaystyle\frac{5}{9}\right)^n+\left(\displaystyle\frac{8}{9}\right)^n-\left(\displaystyle\frac{4}{9}\right)^n
\end{eqnarray}
\ }\)
よって求める確率は
\(\small{
\begin{eqnarray} P\left(\mathrm{A\cap B}\right)&=&1-P\left(\overline{\mathrm{A\cap B}}\right)\\[3pt]
&=&1-\left(\displaystyle\frac{5}{9}\right)^n-\left(\displaystyle\frac{8}{9}\right)^n+\left(\displaystyle\frac{4}{9}\right)^n\\[3pt]
&=&\displaystyle\frac{9^n+4^n-5^n-8^n}{9^n}\end{eqnarray} }\)
次に余事象を利用しない方法で考えてみよう。
余事象を利用しない場合
\(\small{ \ 1 \ }\)回目に\(\small{ \ 5 \ }\)が出て、残りの\(\small{ \ n-1 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回偶数が出る確率は
\(\small{ \ \displaystyle\frac{1}{9}\left\{1-\left(\displaystyle\frac{5}{9}\right)^{n-1}\right\} \ }\)
\(\small{ \ 1 \ }\)回目に偶数が出て、残りの\(\small{ \ n-1 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回\(\small{ \ 5 \ }\)が出る確率は
\(\small{ \ \displaystyle\frac{4}{9}\left\{1-\left(\displaystyle\frac{8}{9}\right)^{n-1}\right\} \ }\)
\(\small{ \ 1 \ }\)回目に\(\small{ \ 5 \ }\)以外の奇数が出て、\(\small{ \ 2 \ }\)回目に\(\small{ \ 5 \ }\)が出て、残りの\(\small{ \ n-2 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回偶数が出る確率は
\(\small{ \ \displaystyle\frac{4}{9}\cdot \displaystyle\frac{1}{9}\left\{1-\left(\displaystyle\frac{4}{9}\right)^{n-2}\right\} \ }\)
\(\small{ \ 1 \ }\)回目に\(\small{ \ 5 \ }\)以外の奇数が出て、\(\small{ \ 2 \ }\)回目に偶数が出て、残りの\(\small{ \ n-2 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回\(\small{ \ 5 \ }\)が出る確率は
\(\small{ \ \displaystyle\frac{4}{9}\cdot\displaystyle\frac{4}{9}\left\{1-\left(\displaystyle\frac{8}{9}\right)^{n-2}\right\} \ }\)
\(\small{ \ 1 \ }\)回目、\(\small{ \ 2 \ }\)回目に\(\small{ \ 5 \ }\)以外の奇数が出て、\(\small{ \ 3 \ }\)回目に\(\small{ \ 5 \ }\)が出て、残りの\(\small{ \ n-3 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回偶数が出る確率は
\(\small{ \ \left(\displaystyle\frac{4}{9}\right)^2\cdot \displaystyle\frac{1}{9}\left\{1-\left(\displaystyle\frac{4}{9}\right)^{n-3}\right\} \ }\)
\(\small{ \ 1 \ }\)回目、\(\small{ \ 2 \ }\)回目に\(\small{ \ 5 \ }\)以外の奇数が出て、\(\small{ \ 3 \ }\)回目に偶数が出て、残りの\(\small{ \ n-3 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回\(\small{ \ 5 \ }\)が出る確率は
\(\small{ \ \left(\displaystyle\frac{4}{9}\right)^2\cdot\displaystyle\frac{4}{9}\left\{1-\left(\displaystyle\frac{8}{9}\right)^{n-3}\right\} \ }\)
同様に
\(\small{ \ 1 \ }\)回目、\(\small{ \ 2 \ }\)回目、\(\small{ \ 3 \ }\)回目に\(\small{ \ 5 \ }\)以外の奇数が出て、\(\small{ \ 4 \ }\)回目に\(\small{ \ 5 \ }\)が出て、残りの\(\small{ \ n-4 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回偶数が出る確率は
\(\small{ \ \left(\displaystyle\frac{4}{9}\right)^3\cdot \displaystyle\frac{1}{9}\left\{1-\left(\displaystyle\frac{4}{9}\right)^{n-4}\right\} \ }\)
\(\small{ \ 1 \ }\)回目、\(\small{ \ 2 \ }\)回目、\(\small{ \ 3 \ }\)回目に\(\small{ \ 5 \ }\)以外の奇数が出て、\(\small{ \ 4 \ }\)回目に偶数が出て、残りの\(\small{ \ n-4 \ }\)回で少なくとも\(\small{ \ 1 \ }\)回\(\small{ \ 5 \ }\)が出る確率は
\(\small{ \ \left(\displaystyle\frac{4}{9}\right)^3\cdot\displaystyle\frac{4}{9}\left\{1-\left(\displaystyle\frac{8}{9}\right)^{n-4}\right\} \ }\)
これを一般化すると
初めから\(\small{ \ k \ }\)回連続で奇数が出て、\(\small{ \ k+1 \ }\)回目に\(\small{ \ 5 \ }\)が出て、残りの\(\small{ \ n-(k+1) \ }\)回で少なくとも\(\small{ \ 1 \ }\)回偶数が出る確率は
\(\small{ \ \left(\displaystyle\frac{4}{9}\right)^k\cdot \displaystyle\frac{1}{9}\left\{1-\left(\displaystyle\frac{4}{9}\right)^{n-k-1}\right\} \ }\)
初めから\(\small{ \ k \ }\)回連続で奇数が出て、\(\small{ \ k+1 \ }\)回目に偶数が出て、残りの\(\small{ \ n-(k+1) \ }\)回で少なくとも\(\small{ \ 1 \ }\)回\(\small{ \ 5 \ }\)が出る確率は
\(\small{ \ \left(\displaystyle\frac{4}{9}\right)^k\cdot \displaystyle\frac{4}{9}\left\{1-\left(\displaystyle\frac{8}{9}\right)^{n-k-1}\right\} \ }\)
よって求める確率は
\left[ \left(\displaystyle\frac{4}{9}\right)^{k} \cdot \displaystyle\frac{1}{9} \left\{1- \left(\displaystyle\frac{5}{9}\right)^{n-k-1}\right\}+ \left(\displaystyle\frac{4}{9}\right)^{k} \cdot \displaystyle\frac{4}{9}\left\{1- \left(\displaystyle\frac{8}{9}\right)^{n-k-1}\right\}\right]}\)
これは
\left[ \left(\displaystyle\frac{4}{9}\right)^{k-1} \cdot \displaystyle\frac{1}{9} \left\{1- \left(\displaystyle\frac{5}{9}\right)^{n-k}\right\}+ \left(\displaystyle\frac{4}{9}\right)^{k-1} \cdot \displaystyle\frac{4}{9}\left\{1- \left(\displaystyle\frac{8}{9}\right)^{n-k}\right\}\right] \ }\)
と同じだから
\left[ \left(\displaystyle\frac{4}{9}\right)^{k-1} \cdot \displaystyle\frac{1}{9} \left\{1- \left(\displaystyle\frac{5}{9}\right)^{n-k}\right\}+ \left(\displaystyle\frac{4}{9}\right)^{k-1} \cdot \displaystyle\frac{4}{9}\left\{1- \left(\displaystyle\frac{8}{9}\right)^{n-k}\right\}\right] \\[3pt] =\displaystyle\sum_{k=1}^{n-1} \left\{ \displaystyle\frac{5}{9}\left(\displaystyle\frac{4}{9}\right)^{k-1}-\displaystyle\frac{1}{9}\left(\displaystyle\frac{4}{9}\right)^{k-1}\left(\displaystyle\frac{5}{9}\right)^{n-k}- \left(\displaystyle\frac{4}{9}\right)^k \left(\displaystyle\frac{8}{9}\right)^{n-k}\right\}\\[3pt] = \displaystyle\sum_{k=1}^{n-1} \left\{ \displaystyle\frac{5}{9}\left(\displaystyle\frac{4}{9}\right)^{k-1}- \displaystyle\frac{1}{9}\left(\displaystyle\frac{5}{9}\right)^{n-1} \left(\displaystyle\frac{4}{9}\right)^{k-1}- \displaystyle\frac{4}{9}\left(\displaystyle\frac{8}{9}\right)^{n-1} \left(\displaystyle\frac{1}{2}\right)^{k-1}\right\}\\[3pt] = \displaystyle\frac{5}{9} \cdot \displaystyle\frac{1- \left(\frac{4}{9}\right)^{n-1}}{1-\frac{4}{9}}-\displaystyle\frac{1}{9}\left(\displaystyle\frac{5}{9}\right)^{n-1}\cdot \displaystyle\frac{1- \left(\frac{4}{5}\right)^{n-1}}{1-\frac{4}{5}}- \displaystyle\frac{4}{9}\left(\displaystyle\frac{8}{9}\right)^{n-1}\cdot \displaystyle\frac{1- \left(\frac{1}{2}\right)^{n-1}}{1-\frac{1}{2}}\\[3pt] =1- \left(\displaystyle\frac{4}{9}\right)^{n-1}-\left(\displaystyle\frac{5}{9}\right)^n \left\{1- \left(\displaystyle\frac{4}{5}\right)^{n-1}\right\}- \left(\displaystyle\frac{8}{9}\right)^n \left\{1- \left(\displaystyle\frac{1}{2}\right)^{n-1}\right\}\\[3pt] =1- \left(\displaystyle\frac{4}{9}\right)^{n-1}- \left(\displaystyle\frac{5}{9}\right)^n+ \displaystyle\frac{5}{4}\left(\displaystyle\frac{4}{9}\right)^n- \left(\displaystyle\frac{8}{9}\right)^n+2 \left(\displaystyle\frac{4}{9}\right)^n\\[3pt] =1- \left(\displaystyle\frac{5}{9}\right)^n- \left(\displaystyle\frac{8}{9}\right)^n+ \left(\displaystyle\frac{4}{9}\right)^n\\[3pt] =\displaystyle\frac{9^n+4^n-5^n-8^n}{9^n} \ }\)
当然余事象を使っても使わなくても答えは同じになるけど、余事象を使わないと計算がすごく大変ってことがわかるよね。確率を直接求めるのが大変だったら、余事象を考えてみよう。
\(\small{ \ n \ }\)人の人がいる。この\(\small{ \ n \ }\)人の中に誕生月が同じ人がいる確率が\(\small{ \ 0.5 \ }\)より大きくなる最小の\(\small{ \ n \ }\)の値を求めよ。ただし、\(\small{ \ n\lt12 \ }\)である。
余事象を考える。
誕生月が同じでない確率は
\(\small{ \ 1-\displaystyle\frac{{}_{12}\mathrm{P}_{n}}{12^{n}} \gt 0.5 \ }\)
\(\small{ \ \displaystyle\frac{{}_{12}\mathrm{P}_{n}}{12^{n}} \lt 0.5 \ }\)
\(\small{ \ \displaystyle\frac{12!}{12^{n}(12-n)!} \lt 0.5 \ }\)
\(\small{ \ n \ }\)は整数であるから、
\(\small{ \ n=4 \ }\)のとき\(\small{ \ \displaystyle\frac{12!}{12^{4}(12-4)!}=0.5729\cdots \ }\)
\(\small{ \ n=5 \ }\)のとき\(\small{ \ \displaystyle\frac{12!}{12^{5}(12-5)!}=0.3819\cdots \ }\)
よって、確率が\(\small{ \ 0.5 \ }\)より大きくなる最小の人数は\(\small{ \ 5 \ }\)人である。

余事象と確率
①「少なくとも」を見たら余事象を考える。
②確率の計算が大変な場合も余事象を考えてみる。
数直線上を原点から出発して次のように駒を動かしていく。各目の出る確率の等しい際うころを\(\small{ \ 1 \ }\)個投げて、\(\small{ \ 1,2 \ }\)が出たときは正の方向へ\(\small{ \ 1 \ }\)だけ動かし、\(\small{ \ 3 ,4, 5, 6 \ }\)が出たときは正の方向へ\(\small{ \ 2 \ }\)動かす。このとき、点\(\small{ \ n \ }\)に止まる確率を\(\small{ \ p_n(n=1, 2,\cdots) \ }\)を\(\small{ \ n \ }\)で表せ。
点\(\small{ \ n \ }\)に止まるのは、点\(\small{ \ n-1 \ }\)に止まって\(\small{ \ 1,2 \ }\)が出るときか、点\(\small{ \ n-2 \ }\)に止まって\(\small{ \ 3 ,4, 5, 6 \ }\)が出るときであるから
\(\small{ \ p_n=\displaystyle\frac{1}{3}p_{n-1}+\displaystyle\frac{2}{3}p_{n-2} \ }\)
が成り立つ。
これを変形すると
\(\small{ \ p_n-p_{n-1}=-\displaystyle\frac{2}{3}(p_{n-1}+p_{n-2}) \ }\)
\(\small{ \ p_1= \displaystyle\frac{1}{3} \ }\)
\(\small{ \ p_2= \left(\displaystyle\frac{1}{3}\right)^2+ \displaystyle\frac{2}{3}= \displaystyle\frac{7}{9} \ }\)
\(\small{
\begin{eqnarray}
p_{n+1}-p_n &=&(p_2-p_1)\left(-\displaystyle\frac{2}{3}\right)^{n-1}\\[3pt]
&=&\displaystyle\frac{4}{9}\left(-\displaystyle\frac{2}{3}\right)^{n-1}
\end{eqnarray}
\ }\)
\(\small{ \ n\geqq2 \ }\)のとき
\(\small{
\begin{eqnarray}
p_n&=&p_1+ \displaystyle\sum_{k=1}^{n-1}\displaystyle\frac{4}{9}\left(-\displaystyle\frac{2}{3}\right)^{k-1}\\[3pt]
&=&\displaystyle\frac{1}{3}+ \displaystyle\frac{4}{9}\cdot\displaystyle\frac{1-\left(-\frac{2}{3}\right)^{n-1}}{1+\frac{2}{3}} \\[3pt]
&=&\displaystyle\frac{3}{5}- \displaystyle\frac{4}{15}\left(-\displaystyle\frac{2}{3}\right)^{n-1}
\end{eqnarray}
\ }\)
これは\(\small{ \ n=1 \ }\)のときも成り立つ。
点\(\small{ \ n \ }\)に止まらない確率は\(\small{ \ 1-p_n \ }\)
点\(\small{ \ n \ }\)に止まらないのは点\(\small{ \ n-1 \ }\)に止まって\(\small{ \ 3 ,4, 5, 6 \ }\)が出るときであるから
\(\small{ \ 1-p_n= \displaystyle\frac{2}{3}p_{n-1} \ }\)
\(\small{ \ p_n=- \displaystyle\frac{2}{3}+1 \ }\)
これを変形して
\(\small{
\begin{eqnarray}
p_n- \displaystyle\frac{3}{5}&=&-\displaystyle\frac{2}{3}\left(p_{n-1}-\displaystyle\frac{3}{5}\right)\\[3pt]
&=&\left(p_1-\displaystyle\frac{3}{5}\right)\left(-\displaystyle\frac{2}{3}\right)^{n-1} \end{eqnarray}}\)
\(\small{ \ p_1= \displaystyle\frac{1}{3} \ }\)より\(\small{ \ p_n=\displaystyle\frac{3}{5}- \displaystyle\frac{4}{15}\left(-\displaystyle\frac{2}{3}\right)^{n-1} \ }\)

-

隣接三項間漸化式
特性方程式の作り方から解の値によって異なる解き方などについて詳しく解説しています。
続きを見る
-

等比数列と特性方程式を利用する隣接二項間漸化式
特性方程式がなぜ成り立つのかなどの疑問について詳しく解説しています。
続きを見る