こんにちは、リンス(@Lins016)です。
今回は球面と平面の交線が作る円について学習していこう。
球面と平面の交線
球面と平面が交わるとき、その交線の描く図形は円になるよね。まずこのことをしっかりと押さえておこう。
今回はこの球面と平面が交わってできる円の方程式や半径を求める問題を平面の法線ベクトルを使ったりして考えていこう。
・軸に垂直な平面と球面の交わり
平面の方程式を球面の方程式に代入
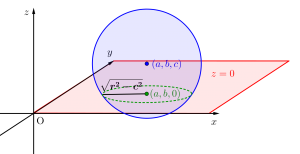
・軸に垂直でない平面と球面の交わり
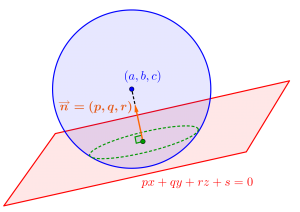
平面の法線ベクトルを利用する
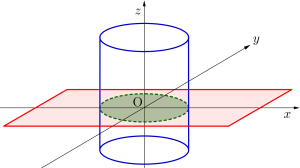
軸に垂直な平面と球の交円
平面の方程式は\(\small{ \ ax+by+cz+d=0 \ }\)が基本だけど、軸に垂直な平面っていうと\(\small{ \ x, \ y, \ z \ }\)の係数のどれか\(\small{ \ 2 \ }\)つが\(\small{ \ 0 \ }\)になるんだ。
例えば\(\small{ \ z \ }\)軸に垂直っていうと\(\small{ \ z=3 \ }\)というような平面になるからね。つまり\(\small{ \ x, \ y \ }\)の係数が\(\small{ \ 0 \ }\)になるってこと。
特に\(\small{ \ z=0 \ }\)の平面のことを\(\small{ \ xy \ }\)平面っていうから覚えておこう。\(\small{ \ x \ }\)軸と\(\small{ \ y \ }\)軸を含む平面だからね。

だから\(\small{ \ y \ }\)軸と\(\small{ \ z \ }\)軸を含む平面は\(\small{ \ x=0 \ }\)平面で\(\small{ \ yz \ }\)平面って呼ばれるし、\(\small{ \ x \ }\)軸と\(\small{ \ z \ }\)軸を含む平面は\(\small{ \ y=0 \ }\)平面で\(\small{ \ xz \ }\)平面って呼ばれるからね。
この平面と球が交わってできる円の方程式は、球の方程式に平面の方程式を代入すればいいんだ。
つまり球の方程式が\(\small{ \ (x-a)^2+(y-b)^2+(z-c)^2=r^2 \ }\)で平面の方程式が\(\small{ \ z=0 \ }\)なら、\(\small{ \ z=0 \ }\)を球の式に代入するってこと。
\(\small{ \ (x-a)^2+(y-b)^2+(0-c)^2=r^2 \ }\)
\(\small{ \ (x-a)^2+(y-b)^2=r^2-c^2 \ }\)
つまり\(\small{ \ z=0 \ }\)平面に中心\(\small{ \ (a, \ b) \ }\)、半径\(\small{ \ \sqrt{r^2-c^2} \ }\)の円ができたってことになるんだ。
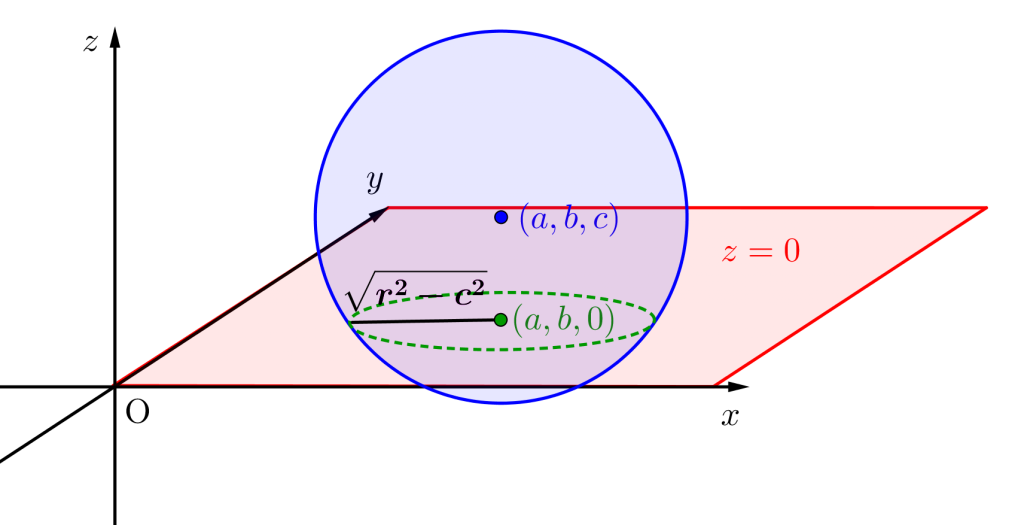
軸に垂直な平面の場合はいつも球の方程式に代入しよう。

交円から球面の方程式を求める
次にさっきとは逆で「交円や平面の方程式が与えられているとき球面の方程式を求める問題」を考えてみよう。
球面の方程式を求めるためには球の中心の座標と球の半径が必要だよね。
この球面の中心と交円の中心の関係を見てみよう。
図を見たら明らかだけど、交円の中心と球の中心を結ぶ線分って平面に垂直になってるんだ。
つまり交円の中心から平面の法線ベクトルを延ばすと球の中心を通るってことね。
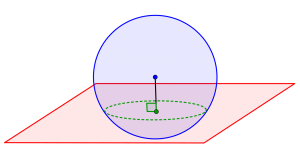
このことって問題を解く上で、すごく重要なことだから覚えておこう。それじゃこれを利用して例題を考えてみよう。
球面\(\small{ \ \mathrm{S} \ }\)と\(\small{ \ xy \ }\)平面との交わりが円\(\small{ \ (x-1)^2+(y-2)^2=40 \ }\)、\(\small{ \ z=0 \ }\)であり、かつ点\(\small{ \ (7, \ 5, \ 5) \ }\)を通る球面の方程式を求めよ。
球面\(\small{ \ \mathrm{S} \ }\)と\(\small{ \ xy \ }\)平面との交わりが\(\small{ \ (x-1)^2+(y-2)^2=40 \ }\)より
球面の方程式は
\(\small{ \ (x-1)^2+(y-2)^2+(z-c)^2=r^2\cdots① \ }\)とおける
\(\small{ \ ① \ }\)に\(\small{ \ z=0 \ }\)を代入して
\(\small{ \ (x-1)^2+(y-2)^2=r^2-c^2 \ }\)
\(\small{ \ \therefore r^2-c^2=40\cdots② \ }\)
\(\small{ \ ① \ }\)は点\(\small{ \ (7, \ 5, \ 5) \ }\)を通るので
\(\small{ \ (7-1)^2+(5-2)^2+(5-c)^2=r^2\cdots③ \ }\)
\(\small{ \ ②、③ \ }\)より
\(\small{ \ c=3, \ r^2=49 \ }\)
よって求める球面の方程式は
\(\small{ \ (x-1)^2+(y-2)^2+(z-3)^2=49 \ }\)

円の方程式は\(\small{ \ (x-1)^2+(y-2)^2=40 \ }\)、\(\small{ \ z=0 \ }\)だから円の中心の座標は\(\small{ \ (1, \ 2, \ 0) \ }\)。
円の中心から法線ベクトルの方向に球面の中心はあるから、球面の方程式は\(\small{ \ (x-1)^2+(y-2)^2+(z-c)^2=r^2 \ }\)っておくことができるんだ。
法線ベクトルと円の半径
次は軸に垂直じゃない平面と球が交わってできる円について考えていこう。
球面の方程式が\(\small{ \ (x-a)^2+(y-b)^2+(z-c)^2=r^2 \ }\)で平面の方程式が\(\small{ \ px+qy+rz+s=0 \ }\)のとき、交円の中心は球の中心を通って、平面の法線ベクトルに平行な直線上にあるよね。

この球の中心と円の中心を通る直線は媒介変数\(\small{ \ t \ }\)を使うと
\(\small{ \ (x, \ y, \ z)=(a, \ b, \ c)+t(p, \ q, \ r) \ }\)
って書ける。これは直線のベクトル方程式の形だよね。
つまりこの直線と平面の交点が円の中心になるから、直線と平面の交点を求めたらいいよね。
これは前回やった直線と平面の交点の求め方を利用するだけだからできるよね。
覚えていないって人がいたら、復習しておこう。
円の中心が分かったら、球の中心と円の中心の距離が求まるから、この距離と球の半径で三平方の定理を利用すれば、円の半径がわかるからね。

球面\(\small{ \ x^2+y^2+z^2-2x-4y+2z-19=0 \ }\)と平面\(\small{ \ 2x+y+2z-11=0 \ }\)がある。
球面と平面の交わりの円の中心と半径を求めよ。
\(\small{ \ x^2+y^2+z^2-2x-4y+2z-19=0 \ }\)
\(\small{ \ (x-1)^2+(y-2)^2+(z+1)^2=25 \ }\)
よって球面の中心の座標は\(\small{ \ (1, \ 2, \ -1) \ }\)
この球面の中心を\(\small{ \ \mathrm{A} \ }\)、求める円の中心を\(\small{ \ \mathrm{B} \ }\)とおくと
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{OB}}&=&\overrightarrow{\mathrm{OA}}+t(2, \ 1, \ 2)\\
&=&(1+2t, \ 2+t, \ -1+2t) \ \end{eqnarray}}\)
これが平面\(\small{ \ 2x+y+2z-11=0 \ }\)上にあるので
\(\small{ \ 2(1+2t)+(2+t)+2(-1+2t)-11=0 \ }\)
これを解いて\(\small{ \ t=1 \ }\)
よって求める円の中心の座標は\(\small{ \ (3, \ 3, \ 1) \ }\)
\(\small{ \ \vert\overrightarrow{\mathrm{AB}}\vert=1\times\vert(2, \ 1, \ 2)\vert \ }\)より
\(\small{ \ \vert\overrightarrow{\mathrm{AB}}\vert=3 \ }\)
よって求める円の半径は
\(\small{ \ \sqrt{5^2-3^2}=4 \ }\)

点と平面の距離の公式使えば球の中心と平面の距離は簡単に求まるからね。
Point 球面と平面の交線が作る円
①軸に垂直な平面は球面の方程式に代入して円の方程式を求める
②球面の中心と交円の中心を結ぶベクトルは、平面の法線ベクトルの実数倍になる
③球面の中心と交円の中心の距離と、円の半径、球面の半径で三平方の定理を利用する
点\(\small{ \ (6, \ 7, \ 2) \ }\)を通る球面\(\small{ \ x^2+y^2+z^2-4x-8y-2az+b=0 \ }\)がある。
(1)この球面が\(\small{ \ xy, \ yz, \ zx \ }\)の各平面から切り取る円の面積の総和の最小値と、そのときの\(\small{ \ a, \ b \ }\)を求めよ。
(2)(1)で求めたそれぞれの円の中心を頂点とする三角形の面積を求めよ。
(1)
これは\(\small{ \ (6, \ 7, \ 2) \ }\)を通るから
\(\small{ \ \therefore b=4a-9 \ }\)
このとき
\(\small{ \ z=0 \ }\)のとき
\(\small{ \ x=0 \ }\)のとき
\(\small{ \ z=0 \ }\)のとき
各座標平面から円が切り取られるためには
\(\small{ \ -4a+29\gt 0 \ }\)
このとき面積の総和を\(\small{ \ f(a) \ }\)とおくと
\(\small{\begin{eqnarray} \ f(a)&=&\pi(2a^2-12a+67)\\
&=&2\pi(a-3)^2+49\pi \ \end{eqnarray}}\)
よって\(\small{ \ a=3 \ }\)のとき最小値\(\small{ \ 49\pi \ }\)
このとき\(\small{ \ b=3 \ }\)
(2)球面の方程式は
\(\small{ \ (x-2)^2+(y-4)^2+(z-3)^2=26 \ }\)
よって各円の中心の座標は
\(\small{ \ \mathrm{A}(2, \ 4, \ 0) \ }\)
\(\small{ \ \mathrm{B}(0, \ 4, \ 3) \ }\)
\(\small{ \ \mathrm{C}(2, \ 0, \ 3) \ }\)
\(\small{ \ \overrightarrow{\mathrm{AB}}=(-2, \ 0, \ 3) \ }\)
\(\small{ \ \overrightarrow{\mathrm{AC}}=(0, \ -4, \ 3) \ }\)
よって求める面積\(\small{ \ \mathrm{S} \ }\)は
&=&\displaystyle\frac{1}{2}\sqrt{13\times25-81}\\
&=&\displaystyle\frac{1}{2}\sqrt{244}\\
&=&\sqrt{61} \ \end{eqnarray}}\)

