こんにちは、リンス(@Lins016)です。
今回は空間ベクトルの内積について学習していこう。
空間ベクトルの内積
空間ベクトルの内積を学習する前に、一度平面ベクトルの内積の記事を読み直しておこう。
内積は二つのベクトルの大きさとなす角で決まるってところは平面ベクトルでも空間ベクトルでも同じだからね。
・内積
\(\small{ \ \overrightarrow{a}\cdot\overrightarrow{b}=\vert\overrightarrow{a}\vert \vert\overrightarrow{b}\vert\cos\theta \ }\)
・成分表示
\(\small{ \ \overrightarrow{a}=(a_1, \ a_2, \ a_3) \ }\)、\(\small{ \ \overrightarrow{b}=(b_1, \ b_2, \ b_3) \ }\)
\(\small{ \ \overrightarrow{a}\cdot \overrightarrow{b}=a_1b_1+a_2b_2+a_3b_3 \ }\)
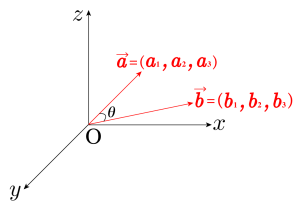
成分と内積
平面ベクトルの内積と異なるのは、空間ベクトルの成分表示は\(\small{ \ x \ }\)成分、\(\small{ \ y \ }\)成分、\(\small{ \ z \ }\)成分の\(\small{ \ 3 \ }\)つの成分があることだよね。
だから平面ベクトルの内積の計算がそのまま有効ってわけにはいかないんだけど、大きく変わることもないんだ。
平面ベクトルでは\(\small{ \ \overrightarrow{\mathrm{OA}}=(a_1, \ a_2) \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}}=(b_1, \ b_2) \ }\)の内積は
\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=a_1b_1+a_2b_2 \ }\)だったよね。
これが空間ベクトルでは
\(\small{ \ \overrightarrow{\mathrm{OA}}=(a_1, \ a_2, \ a_3) \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}}=(b_1, \ b_2, \ b_3) \ }\)の内積は
\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=a_1b_1+a_2b_2+a_3b_3 \ }\)になるんだ。
つまり単に\(\small{ \ z \ }\)成分の計算が増えてだけだよね。だから空間ベクトルでも成分の問題は成分のまま解くようにしよう。計算が少し増えるだけだからね。
平面ベクトルの内積の記事も確認しておこう。
二つのベクトル\(\small{ \ \vec{a}=(1, \ 2, \ 3) \ }\)、\(\small{ \ \vec{b}=(1, \ -2, \ 1) \ }\)の両方に垂直な単位ベクトルを求めよ。
\(\small{ \ \vec{a} \ }\)、\(\small{ \ \vec{b} \ }\)に垂直な単位ベクトルを\(\small{ \ \vec{p}=(x, \ y, \ z) \ }\)とすると
\(\small{ \ \vec{a}\cdot\vec{p}=0 \ }\)より
\(\small{ \ x+2y+3z=0\cdots① \ }\)
\(\small{ \ \vec{b}\cdot\vec{p}=0 \ }\)より
\(\small{ \ x-2y+z=0\cdots② \ }\)
\(\small{ \ \vec{p} \ }\)は単位ベクトルより
\(\small{ \ x^2+y^2+z^2=1\cdots③ \ }\)
\(\small{ \ ①②③ \ }\)を連立して解くと
\(\small{ \ \vec{p}=\pm\left(\displaystyle\frac{1}{\sqrt{3}}, \ \displaystyle\frac{1}{\sqrt{3}}, \ \displaystyle\frac{1}{\sqrt{3}}\right) \ }\)
外積を使って考えてみると
\(\small{ \ \vec{a}=(2, \ 1, \ -3) \ }\)、\(\small{ \ \vec{b}=(1, \ -2, \ 1) \ }\)のとき
&=&(-5, \ -5, \ -5) \ \end{eqnarray}}\)
外積\(\small{ \ \vec{a}\times \vec{b} \ }\)は\(\small{ \ \vec{a} \ }\)、\(\small{ \ \vec{b} \ }\)に垂直なので、このベクトルの単位ベクトルが求める値になる
\(\small{ \ \displaystyle\frac{(-5, \ -5, \ -5)}{\sqrt{(-5)^2+(-5)^2+(-5)^2}}\\
=\left(-\displaystyle\frac{1}{\sqrt{3}}, \ -\displaystyle\frac{1}{\sqrt{3}}, \ -\displaystyle\frac{1}{\sqrt{3}}\right) \ }\)
垂直なベクトルは逆向きもあるから求めるベクトルは
\(\small{ \ \pm\left(\displaystyle\frac{1}{\sqrt{3}}, \ \displaystyle\frac{1}{\sqrt{3}}, \ \displaystyle\frac{1}{\sqrt{3}}\right) \ }\)

\(\small{ \ \vec{a}=(a_1, \ a_2, \ a_3) \ }\)、\(\small{ \ \vec{a}=(b_1, \ b_2, \ b_3) \ }\)のとき
外積\(\small{ \ \vec{a}\times \vec{b} \ }\)は次のようになるからね。
\(\small{ \ \vec{a}\times \vec{b}=(a_2b_3-a_3b_2, \ a_3b_1-a_1b_3, \ a_1b_2-a_2b_1) \ }\)
三つの基準のベクトルと内積
平面ベクトルでは二つの基準のベクトル(例えば\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\))でその他のベクトルを\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ }\)のように表したよね。
平面ベクトルをきちんと勉強した人はわかると思うけど、平面ベクトルの内積を利用する問題を解くとき、基準のベクトルの大きさと内積が必要になるんだ。
つまり基準のベクトルが\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)なら\(\small{ \ \vert\overrightarrow{\mathrm{OA}}\vert \ }\)と\(\small{ \ \vert\overrightarrow{\mathrm{OB}}\vert \ }\)と\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}} \ }\)の\(\small{ \ 3 \ }\)つが必要だったよね。
これが\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)を基準とする空間ベクトルの内積を利用する問題になると、\(\small{ \ \vert\overrightarrow{\mathrm{OA}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OB}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OC}}\vert \ }\)と\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}}\cdot \overrightarrow{\mathrm{OC}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}} \ }\)の\(\small{ \ 6 \ }\)つが必要になる。
例えば\(\small{ \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)のとき\(\small{ \ \overrightarrow{\mathrm{OP}} \ }\)の大きさは
&=&s^2\vert\overrightarrow{\mathrm{OA}}\vert^2+t^2\vert\overrightarrow{\mathrm{OB}}\vert^2+u^2\vert\overrightarrow{\mathrm{OC}}\vert^2+2\left(\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OB}}\cdot \overrightarrow{\mathrm{OC}}\right) \ \end{eqnarray}}\)
になるんだ。
一気に計算量が増えた気がするけど、当然\(\small{ \ 3 \ }\)つのベクトルを利用するわけだから、大きさも\(\small{ \ 3 \ }\)つあるし、内積も\(\small{ \ 3 \ }\)つあるに決まってるよね。計算が複雑で大変になるけど、丁寧に計算していこう。
空間の\(\small{ \ 3 \ }\)つのベクトル\(\small{ \ \vec{a} \ }\)、\(\small{ \ \vec{b} \ }\)、\(\small{ \ \vec{c} \ }\)に対して、\(\small{ \ \vert\vec{a}\vert=6 \ }\)、\(\small{ \ \vert\vec{c}\vert=1 \ }\)、\(\small{ \ \vec{a} \ }\)と\(\small{ \ \vec{b} \ }\)のなす角は\(\small{ \ 60^{\circ} \ }\)である。また、\(\small{ \ \vec{a} \ }\)と\(\small{ \ \vec{c} \ }\)、\(\small{ \ \vec{b} \ }\)と\(\small{ \ \vec{c} \ }\)、\(\small{ \ \vec{a}+\vec{b}+\vec{c} \ }\)と\(\small{ \ 2\vec{a}-5\vec{b} \ }\)はどれも垂直である。
\(\small{ \ \vert\vec{b}\vert \ }\)、\(\small{ \ \vert\vec{a}+\vec{b}+\vec{c}\vert \ }\)を求めよ。
\(\small{ \ \vec{a}\cdot\vec{b}=\vert\vec{a}\vert\vert\vec{b}\vert\cos60^{\circ}=3\vert\vec{b}\vert\cdots① \ }\)
\(\small{ \ \vec{a}\cdot\vec{c}=0\cdots② \ }\)
\(\small{ \ \vec{b}\cdot\vec{c}=0\cdots③ \ }\)
\(\small{ \ \left(\vec{a}+\vec{b}+\vec{c}\right)\cdot\left(2\vec{a}-5\vec{b}\right)=0\cdots④ \ }\)
\(\small{ \ ④ }\)より
\(\small{ \ 2\vert\vec{a}\vert^2-5\vert\vec{b}\vert^2-3\vec{a}\cdot\vec{b}+2\vec{a}\cdot\vec{c}-5\vec{b}\cdot\vec{c}=0 \ }\)
\(\small{ \ 72-5\vert\vec{b}\vert^2-9\vert\vec{b}\vert=0 \ }\)
\(\small{ \ 5\vert\vec{b}\vert^2+9\vert\vec{b}\vert-72=0 \ }\)
\(\small{ \ \left(\vert\vec{b}\vert-3\right)\left(5\vert\vec{b}\vert+24\right)=0 \ }\)
\(\small{ \ \vert\vec{b}\vert\gt0 \ }\)より\(\small{ \ \vert\vec{b}\vert=3 \ }\)
\(\small{ \ \vert\vec{a}+\vec{b}+\vec{c}\vert^2\\
=\vert\vec{a}\vert^2+\vert\vec{b}\vert^2+\vert\vec{c}\vert^2+2\left(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}+\vec{a}\cdot\vec{c}\right)\\
=36+9+1+2\times9\\
=64 \ }\)
\(\small{ \ \therefore \vert\vec{a}+\vec{b}+\vec{c}\vert=8 \ }\)

Point 空間ベクトルの内積
①成分の問題は成分で解く
②基準のベクトルが3つある問題の場合、大きさ3つと内積3つが必要
\(\small{ \ 1 \ }\)辺の長さが\(\small{ \ 1 \ }\)の正四面体\(\small{ \ \mathrm{OABC} \ }\)において、\(\small{ \ 2 \ }\)辺\(\small{ \ \mathrm{AB} \ }\)、\(\small{ \ \mathrm{OC} \ }\)の中点をそれぞれ\(\small{ \ \mathrm{M} \ }\)、\(\small{ \ \mathrm{N} \ }\)とする。次の問いに答えよ。
(1)\(\small{ \ \overrightarrow{\mathrm{MN}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{BN}} \ }\)の内積を求めよ。
(2)\(\small{ \ \angle \mathrm{BNM}=\theta \ }\)とするとき、\(\small{ \ \cos\theta \ }\)の値を求めよ。
(1)
\(\small{ \ \overrightarrow{\mathrm{OM}}=\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{OA}}+\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \ }\)
\(\small{ \ \overrightarrow{\mathrm{ON}}=\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{OC}} \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{MN}}&=&\overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{OM}}\\
&=&\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{OC}}-\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{OA}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{BN}}&=&\overrightarrow{\mathrm{ON}}-\overrightarrow{\mathrm{OB}}\\
&=&\displaystyle\frac{1}{2 }\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}} \ \end{eqnarray}}\)
\(\small{ \ 1 \ }\)辺が\(\small{ \ 1 \ }\)の正四面体だから
\(\small{ \ \vert \overrightarrow{\mathrm{OA}} \vert= \vert \overrightarrow{\mathrm{OB}} \vert= \vert \overrightarrow{\mathrm{OC}} \vert=1 \ }\)
\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB}}\cdot \overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}}=\displaystyle\frac{1}{2} \ }\)
=\displaystyle\frac{1}{2}\left(\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\right)\cdot \displaystyle\frac{1}{2}\left(\overrightarrow{\mathrm{OC}}-2\overrightarrow{\mathrm{OB}}\right)\\
=\displaystyle\frac{1}{4}\left(\vert \overrightarrow{\mathrm{OC}} \vert^2+2\vert \overrightarrow{\mathrm{OB}} \vert^2+2\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}}-3\overrightarrow{\mathrm{OB}}\cdot \overrightarrow{\mathrm{OC}} \right)\\
=\displaystyle\frac{1}{2} \ }\)
(2)
\(\small{ \ \cos\theta=\displaystyle\frac{ \overrightarrow{\mathrm{MN}} \cdot \overrightarrow{\mathrm{BN}} }{ \vert \overrightarrow{\mathrm{MN}} \vert \vert \overrightarrow{\mathrm{BN}} \vert } \ }\)
=\displaystyle\frac{1}{4}\vert\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\vert^2\\
=\displaystyle\frac{1}{4}\left\{\vert\overrightarrow{\mathrm{OA}}\vert^2+\vert\overrightarrow{\mathrm{OB}}\vert^2+\vert\overrightarrow{\mathrm{OC}}\vert^2+2\left(\overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OB}} \cdot \overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}} \cdot \overrightarrow{\mathrm{OC}}\right)\right\}\\
=\displaystyle\frac{1}{2} \ }\)
\(\small{ \ \vert \overrightarrow{\mathrm{BN}} \vert^2\\
=\displaystyle\frac{1}{4}\vert\overrightarrow{\mathrm{OC}}-2\overrightarrow{\mathrm{OB}}\vert^2\\
=\displaystyle\frac{1}{4}\left(4\vert\overrightarrow{\mathrm{OB}}\vert^2+\vert\overrightarrow{\mathrm{OC}}\vert^2-4\overrightarrow{\mathrm{OB}} \cdot \overrightarrow{\mathrm{OC}}\right)\\
=\displaystyle\frac{3}{4} \ }\)
\(\small{ \ \cos\theta=\displaystyle\frac{ \overrightarrow{\mathrm{MN}} \cdot \overrightarrow{\mathrm{BN}} }{ \vert \overrightarrow{\mathrm{MN}} \vert \vert \overrightarrow{\mathrm{BN}} \vert }\\
=\displaystyle\frac{\displaystyle\frac{1}{2}}{\displaystyle\frac{1}{\sqrt{2}}\cdot\displaystyle\frac{\sqrt{3}}{2}}\\[14pt]
=\displaystyle\frac{\sqrt{6}}{3} \ }\)

そうするとベクトルの大きさや内積を計算する部分は分数の係数がなくなって計算が楽になるね。
=\displaystyle\frac{1}{2}\left(\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\right)\cdot \displaystyle\frac{1}{2}\left(\overrightarrow{\mathrm{OC}}-2\overrightarrow{\mathrm{OB}}\right)\\
=\displaystyle\frac{1}{4}\left(\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\right)\cdot \left(\overrightarrow{\mathrm{OC}}-2\overrightarrow{\mathrm{OB}}\right) \ }\)
分数の計算は計算ミスもしやすいから、この計算方法を利用していこう。

