こんにちは、リンス(@Lins016)です。
今回は空間ベクトルの成分表示と空間座標とその解き方について学習していこう。
空間ベクトルの成分表示は
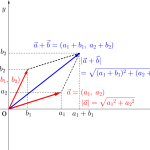
ベクトルって大きさと向きがあるものだったよね。これをよりわかりやすくしたものに成分表示のベクトルがある。
平面ベクトルの場合とそう大きく変わらないから、まずは平面ベクトルの成分表示を復習しておこう。
-

平面ベクトルの成分表示とその解き方
成分表示されたベクトルの考え方や解き方について詳しく解説しています。
続きを見る
平面のとき\(\small{ \ (x, \ y) \ }\)だったけど、今回は空間になるから\(\small{ \ (x, \ y, \ z) \ }\)になるよね。
でも計算の方法は平面のときと変わらないから、単純に\(\small{ \ z \ }\)方向の成分の分だけ計算量が増えるって事になるかな。
空間ベクトルの計算や解き方をきちんと押さえておこう。
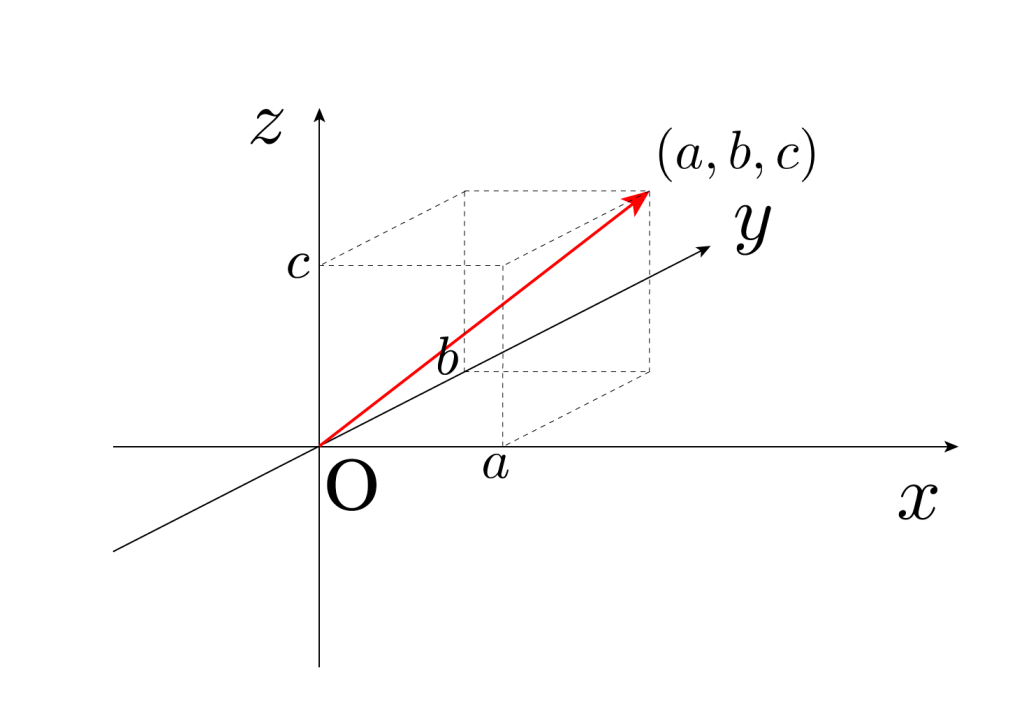
空間ベクトルの成分表示とその解き方
まず頭に入れておいて欲しいことがある。
それは平面ベクトルのときも言ったけど「問題文が成分表示のときは成分表示を利用して解く」ということ。
問題が成分表示のベクトルで書いてあるのに、わざわざ文字で表記するベクトル(\(\small{ \ \overrightarrow{ \mathrm{OA} } \ }\)や\(\small{ \ \vec{a} \ }\))で問題を解いたりしないようにね。
成分表示のベクトルの問題は成分表示のまま解こう。
成分表示されたベクトルの実数倍
平面ベクトルの時と同様に、空間ベクトルでもベクトルを伸ばしたり縮めたりする場合、実数\(\small{ \ k \ }\)を使って\(\small{ \ k \vec{a} \ }\)って書くからね。
成分表示の場合は\(\small{ \ \vec{a}=(a_1, \ a_2, \ a_3) \ }\)を\(\small{ \ k \ }\)倍すると\(\small{ \ k\vec{a}=k(a_1, \ a_2, \ a_3)=(ka_1, \ ka_2, \ ka_3) \ }\)になる。
これも平面ベクトルのときと一緒だからね。
成分表示されたベクトルの和と差
成分表示された二つのベクトル\(\small{ \ \vec{a}=(a_1, \ a_2, \ a_3) \ }\)と\(\small{ \ \vec{b}=(b_1, \ b_2, \ b_3) \ }\)の和について考えてみよう。
成分表示のベクトルの場合\(\small{ \ x \ }\)成分と\(\small{ \ y \ }\)成分と\(\small{ \ z \ }\)成分をそれぞれ足せばいいから
\(\small{\begin{eqnarray} \ \vec{a}+\vec{b}&=&(a_1, \ a_2, \ a_3)+(b_1, \ b_2, \ b_3)\\
&=&(a_1+b_1, \ a_2+b_2, \ a_3+b_3) \ \end{eqnarray}}\)
になる。
これも平面ベクトルのときと同じで、単純に\(\small{ \ z \ }\)成分が加わったってことになるからね。
今度は成分表示された二つのベクトル\(\small{ \ \vec{a}=(a_1, \ a_2, \ a_3) \ }\)と\(\small{ \ \vec{b}=(b_1, \ b_2, \ b_3) \ }\)の差について考えてみよう。
成分表示のベクトルの場合\(\small{ \ x \ }\)成分と\(\small{ \ y \ }\)成分をそれぞれ引けばいいから
\(\small{\begin{eqnarray} \ \vec{a}-\vec{b}&=&(a_1, \ a_2, \ a_3)-(b_1, \ b_2, \ b_3)\\
&=&(a_1-b_1, \ a_2-b_2, \ a_3-b_3) \ \end{eqnarray}}\)
になる。
これも単純に\(\small{ \ z \ }\)成分が加わっただけだよね。
\(\small{ \ \vec{a}=(1, \ 2, \ 3) \ }\)、\(\small{ \ \vec{b}=(0, \ 2, \ 5) \ }\)、\(\small{ \ \vec{c}=(1, \ 3, \ 1) \ }\)のとき、\(\small{ \ \vec{p}=(0, \ 3, \ 12) \ }\)を\(\small{ \ \vec{a}, \ \vec{b}, \ \vec{c} \ }\)を用いて表せ。
\(\small{ \ \vec{p}=s\vec{a}+t\vec{b}+u\vec{c} \ }\)とすると
&=&(s+u, \ 2s+2t+3u, \ 3s+5t+u) \ \end{eqnarray}}\)
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
s+u=0 \\
2s+2t+3u=3\\
3s+5t+u=12
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて
\(\small{ \ s=1, \ t=2, \ u=-1 \ }\)
\(\small{ \ \therefore \vec{p}=\vec{a}+2\vec{b}-\vec{c} \ }\)

空間中のベクトルは同一平面上にない三つのベクトルを用いて
\(\small{ \ \overrightarrow{\mathrm{OP}}=s \overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u \overrightarrow{\mathrm{OC}} \ }\)で表すことが出来るからね。
-

空間ベクトルの基本
空間ベクトルの表し方などついて詳しく解説しています。
続きを見る
成分表示されたベクトルの大きさ
成分表示されたベクトル\(\small{ \ \vec{a}=(a_1, \ a_2, \ a_3) \ }\)の大きさについて考えてみよう。
成分表示されたベクトルの大きさは三平方の定理定理を利用すると簡単に求めることができる。
成分表示は\(\small{ \ x \ }\)成分と\(\small{ \ y \ }\)成分と\(\small{ \ z \ }\)成分の移動量を表しているから、それぞれの値を\(\small{ \ 2 \ }\)乗して足せば、そのベクトルの大きさの\(\small{ \ 2 \ }\)乗になる。
\(\small{ \ \vec{a}= {a_1}^2+{a_2}^2+{a_3}^2 \ }\)
\(\small{ \ \therefore | \vec{a}|= \sqrt{{a_1}^2+{a_2}^2+{a_3}^2} \ }\)
\(\small{ \ \vec{a}+\vec{b}=(a_1+b_1, \ a_2+b_2, \ a_3+b_3) \ }\)の大きさは
になる。
\(\small{ \ \vec{a}=(0, \ -4, \ 2) \ }\)、\(\small{ \ \vec{b}=(2, \ 1, \ -1) \ }\)のとき、\(\small{ \ \vec{x}=\vec{a}+t\vec{b} \ }\)(\(\small{ \ t \ }\)は実数)の大きさが最小となる\(\small{ \ \vec{x} \ }\)を求めよ。
\(\small{\vec{x}=\vec{a}+t\vec{b} \ }\)より
\(\small{\begin{eqnarray}\vec{x}&=&(0, \ -4, \ 2)+t(2, \ 1, \ -1)\\
&=&(2t, \ t-4, \ -t+2) \ \end{eqnarray}}\)
\(\small{\begin{eqnarray}|\vec{x}|^2&=&(2t)^2+(t-4)^2+(-t+2)^2\\
&=&6t^2-12t+20\\
&=&6(t-1)^2+14 \ \end{eqnarray}}\)
\(\small{t=1 \ }\)のとき\(\small{ \ \vec{x} \ }\)の大きさは最小
よって\(\small{ \ \vec{x}=(2, \ -3, \ 1) \ }\)

これは\(\small{ \ \vec{x}=(2t, \ t-4, \ -t+2) \ }\)からも媒介変数の軌跡とも言えるよね。
平面ベクトルの場合だと媒介変数を消去して\(\small{ \ ax+by+c=0 \ }\)の直線の形に変形できたよね。

空間だと\(\small{ \ \vec{x}=(x, \ y, \ z)=(2t, \ t-4, \ -t+2) \ }\)から\(\small{ \ t=\displaystyle\frac{x}{2}=\displaystyle\frac{y+4}{1}=\displaystyle\frac{z-2}{-1} \ }\)に変形して
\(\small{ \ \displaystyle\frac{x}{2}=y+4=-z+2 \ }\)を直線の方程式っていうからね。
これについてはまた今度空間ベクトルのベクトル方程式で勉強しよう。
-

媒介変数で表された軌跡の方程式
媒介変数で表された軌跡の求め方について詳しく解説しています。
続きを見る
空間座標と対称点
空間座標の問題は空間ベクトルの成分の問題として考えることが出来るよね。
この空間座標では意外と対称点を利用することがあるから対称点についても考えておこう。
対称と言えば点対称、軸対称、面対称があるかな。
それぞれの対称でどう座標が変化するのか覚えておこう。
原点対称
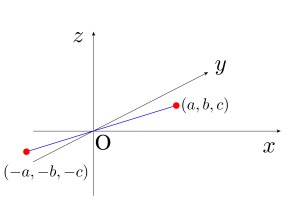
全ての成分の符号が逆になる
点対称
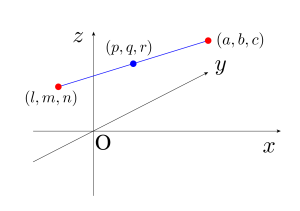
対称点が中点になる
\(\small{ \ (p,q,r)=\left(\displaystyle\frac{a+l}{2},\displaystyle\frac{b+m}{2},\displaystyle\frac{c+n}{2}\right) \ }\)
軸対称
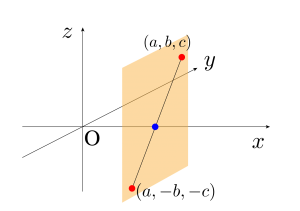
対称軸(この図の場合\(\small{ \ x \ }\)軸)の成分以外の符号が逆になる
面対称
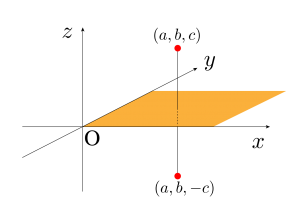
対称面(この図の場合\(\small{ \ xy \ }\)平面)以外の成分(\(\small{ \ z \ }\)成分)の符号が逆になる
点\(\small{ \ \mathrm{P} \ }\)を\(\small{ \ xy \ }\)平面に対称移動し、更に\(\small{ \ y \ }\)軸に対称移動すると、座標が\(\small{ \ (2, \ 3, \ -1) \ }\)になった。点\(\small{ \ \mathrm{P} \ }\)の座標を求めよ。
点\(\small{ \ \mathrm{P} \ }\)の座標を\(\small{ \ (p, \ q, \ r) \ }\)とする
\(\small{ \ xy \ }\)平面に対称移動すると\(\small{ \ (p, \ q, \ -r) \ }\)
更に\(\small{ \ y \ }\)軸に対称移動すると\(\small{ \ (-p, \ q, \ r) \ }\)
\(\small{ \ (-p, \ q, \ r)=(2, \ 3, \ -1) \ }\)より
\(\small{ \ (p, \ q, \ r)=(-2, \ 3, \ -1) \ }\)
空間座標と図形の描画
空間図形を描くときに成分や座標で表示されていると、図のように\(\small{ \ x \ }\)軸\(\small{ \ y \ }\)軸\(\small{ \ z \ }\)軸をきちんと書いて図形を描きたくなるよね。
でも本当に\(\small{ \ x \ }\)軸\(\small{ \ y \ }\)軸\(\small{ \ z \ }\)軸って必要かな?
わざわざ目盛りをとって正確な座標に点を描いても実際はあんまり意味ないよね。だって正確な図が描けないと問題が解けないわけじゃないから。
つまり問題を解く上で考えやすいように図を描いてるだけで、必ず問題を解くのに必要ってわけじゃないんだ。
正確な図が必要じゃないってなると\(\small{ \ x \ }\)軸\(\small{ \ y \ }\)軸\(\small{ \ z \ }\)軸ってわざわざ書かなくても良さそうだよね。基準のベクトルを三つ描いて、それで問題を考えたら良さそうだもんね。
むしろたいして利用しない\(\small{ \ x \ }\)軸\(\small{ \ y \ }\)軸\(\small{ \ z \ }\)軸を書くことで、図が見にくくなって問題が考えにづらくなる可能性だってあるんだ。
だから必ずしも\(\small{ \ x \ }\)軸\(\small{ \ y \ }\)軸\(\small{ \ z \ }\)軸を描かなくてもいいからね。各軸は問題に合わせて必要なときにだけ描くようにしよう。
Point 空間ベクトルの成分表示と空間座標とその解き方
①平面ベクトルも空間ベクトルも成分表示の問題は成分表示のまま解く
②成分表示されたベクトルの和や差、実数倍を丁寧に計算する
③対称な点の求め方を覚える
④図形の描写に各軸はなくてもOK