こんにちは、リンス(@Lins016)です。
今回は空間ベクトルを利用した四面体の体積の求め方(成分表示)について学習していこう。
成分表示の四面体の体積の求め方
前回学習した成分表示じゃない四面体の体積の求め方と同じで、成分表示でも「底面積×高さ×\(\small{ \ \displaystyle\frac{1}{3} \ }\)」を利用するんだ。
ただ、高さにあたる垂線の長さの求め方の計算を少しでも簡単に出来ないか考えていこう。
四面体の体積
\(\small{ \ \mathrm{V}=\displaystyle\frac{1}{3}\times \mathrm{S_{\triangle BCD}}\times \left|\overrightarrow{\mathrm{AH}}\right| \ }\)
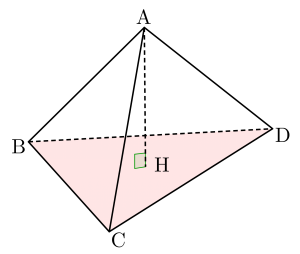
底面積の求め方
成分表示の問題でも底面積の求め方は面積の公式を利用して求めよう。
四面体\(\small{ \ \mathrm{ABCD} \ }\)を求める場合、底面を\(\small{ \ \triangle \mathrm{BCD} \ }\)として、その面積\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{BC}}\vert^2 \ \vert\overrightarrow{\mathrm{BD}}\vert^2-\left(\overrightarrow{\mathrm{BC}}\cdot\overrightarrow{\mathrm{BD}}\right)^2} \ }\)

これを使えばいいから、各ベクトルを成分表示で求めて計算しよう。
垂線の長さの求め方
成分表示でも垂線の長さが高さになるんだけど、この垂線の長さの求め方が成分表示だと色々あるんだ。どの方法で求めてもいいけど、出来るだけ計算が楽な方がいいよね。
四面体\(\small{ \ \mathrm{ABCD} \ }\)を求める場合、頂点\(\small{ \ \mathrm{A} \ }\)から平面\(\small{ \ \mathrm{BCD} \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)として\(\small{ \ \mathrm{AH} \ }\)の長さを求める方法について考えてみよう。
①基本の方法
成分表示じゃない問題と同じで基準のベクトルを\(\small{ \ \overrightarrow{\mathrm{AB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{AC}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{AD}} \ }\)として、
\(\small{ \ \overrightarrow{\mathrm{AH}}=s\overrightarrow{\mathrm{AB}}+t\overrightarrow{\mathrm{AC}}+u\overrightarrow{\mathrm{AD}} \ }\)から
\(\small{ \ \begin{eqnarray}
\left\{
\begin{array}{l}
s+t+u=1\\
\overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BC}}=0\\
\overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{BD}}=0
\end{array}
\right.
\end{eqnarray} \ }\)
の\(\small{ \ 3 \ }\)つの式を連立して\(\small{ \ s, \ t, \ u \ }\)を求める方法ね。
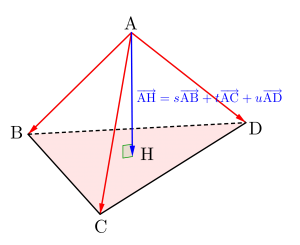
この方法は一番計算量が多くて大変だからあまりオススメしないかな。でも成分表示じゃない問題では使う方法だから覚えておかないといけないよ。
②平面の法線ベクトルを利用する方法
成分表示だと点\(\small{ \ \mathrm{B} \ }\)、点\(\small{ \ \mathrm{C} \ }\)、点\(\small{ \ \mathrm{D} \ }\)の座標が分かっているから、この\(\small{ \ 3 \ }\)点を通る平面の方程式を求めよう。
平面の方程式が求まるとその方程式の係数から法線ベクトルが求まるよね。
これを利用して垂線の足の座標や垂線の長さを求めよう。
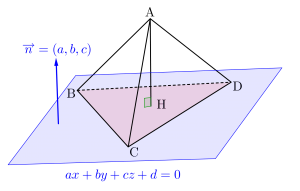
この方法については次の記事で垂線の長さを求める方法を詳しく解説してるから確認しておこう。
③外積を利用する方法
外積を利用して、いきなり垂線の長さがでるわけじゃないからね。
底面をつくる\(\small{ \ 2 \ }\)つのベクトルの外積はその\(\small{ \ 2 \ }\)つのベクトルに垂直なベクトルになるから、②の法線ベクトルを求めることと同じ考え方になるんだ。
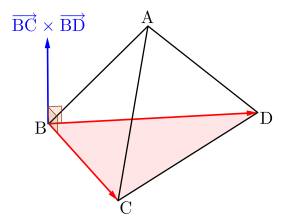
っ言っても外積って記述試験に使えないからあくまで②の法線ベクトルを求めてそれがあっているか確認するための検算に利用しよう。
ただ外積と法線ベクトルは平行だけど同じ大きさのベクトルになるとは限らないから注意しよう。
体積の公式の利用
最後に求めた値から体積の公式
\(\small{ \ \mathrm{V}=\displaystyle\frac{1}{3}\times \mathrm{S_{\triangle BCD}} \times \left|\overrightarrow{\mathrm{AH}}\right| \ }\)
に代入して体積を求めよう。
原点\(\small{ \ \mathrm{O} \ }\)と\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{A}(1, \ -2, \ 3) \ }\)、\(\small{ \ \mathrm{B}(-1, \ 2, \ 3) \ }\)、\(\small{ \ \mathrm{C}(1, \ 2, \ -3) \ }\)を頂点とする四面体\(\small{ \ \mathrm{OABC} \ }\)の体積を求めよ。
原点\(\small{ \ \mathrm{O} \ }\)から平面\(\small{ \ \mathrm{ABC} \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)とすると
&=&s(1, \ -2, \ 3)+t(-1, \ 2, \ 3)+u(1, \ 2, \ -3)\\
&=&(s-t+u, \ -2s+2t+2u, \ 3s+3t-3u) \ \end{eqnarray}}\)
\(\small{ \ \mathrm{H} \ }\)は平面\(\small{ \ \mathrm{ABC} \ }\)より
\(\small{ \ s+t+u=1\cdots① \ }\)
平面\(\small{ \ \mathrm{ABC} \ }\)と\(\small{ \ \overrightarrow{\mathrm{OH}} \ }\)は垂直より
\(\small{ \ \overrightarrow{\mathrm{OH}}\cdot\overrightarrow{\mathrm{AB}}=0 \ }\)
\(\small{ \ -5s+5t+3u=0\cdots② \ }\)
\(\small{ \ \overrightarrow{\mathrm{OH}}\cdot\overrightarrow{\mathrm{AC}}=0 \ }\)
\(\small{ \ -13s-5t+13u=0\cdots③ \ }\)
\(\small{ \ ①, \ ②, \ ③ \ }\)を解いて
\(\small{ \ s=\displaystyle\frac{20}{49}, \ t=\displaystyle\frac{13}{98}, \ u=\displaystyle\frac{45}{98} \ }\)
これより
\(\small{ \ \overrightarrow{\mathrm{OH}}=\left(\displaystyle\frac{36}{49}, \ \displaystyle\frac{18}{49}, \ \displaystyle\frac{12}{49}\right) \ }\)
\(\small{\begin{eqnarray} \ \left|\overrightarrow{\mathrm{OH}}\right|&=&\left|\displaystyle\frac{6}{49}\left(6, \ 3, \ 2\right)\right|\\
&=&\displaystyle\frac{6}{49}\sqrt{6^2+3^2+2^2}\\
&=&\displaystyle\frac{6}{7} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{AB}}=(-2, \ 4, \ 0) \ }\)、\(\small{ \ \overrightarrow{\mathrm{AC}}=(0, \ 4, \ -6) \ }\)より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\left|\overrightarrow{\mathrm{AB}}\right|=\sqrt{2^2+4^2}=2\sqrt{5}\\
\left|\overrightarrow{\mathrm{AC}}\right|=\sqrt{4^2+(-6)^2}=2\sqrt{13}\\
\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}=16
\end{array}
\right.
\end{eqnarray} \ }\)
&=&14 \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \mathrm{V}&=&\displaystyle\frac{1}{3}\times14\times\displaystyle\frac{6}{7}\\
&=&4 \ \end{eqnarray}}\)
点\(\small{ \ \mathrm{A}(1, \ -2, \ 3) \ }\)を通る平面の方程式は
\(\small{ \ a(x-1)+b(y+2)+c(z-3)=0 \ }\)
これは\(\small{ \ \mathrm{B}(-1, \ 2, \ 3) \ }\)、\(\small{ \ \mathrm{C}(1, \ 2, \ -3) \ }\)も通るので
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
-2a+4b=0\\
4b-6c=0
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて\(\small{ \ a=2b=3c \ }\)
よって\(\small{ \ \mathrm{A, \ B, \ C} \ }\)を通る平面の方程式は
\(\small{ \ 6x+3y+2z-6=0 \ }\)
この平面の法線ベクトルは\(\small{ \ (6, \ 3, \ 2) \ }\)
原点を通りこの法線ベクトルに平行な直線と平面\(\small{ \ \mathrm{ABC} \ }\)の交点が垂線の足となる
直線上の点は媒介変数\(\small{ \ t \ }\)を利用して
\(\small{\begin{eqnarray} \ (x, \ y, \ z)&=&t(6, \ 3, \ 2)\\
&=&(6t, \ 3t, \ 2t) \ \end{eqnarray}}\)
これを平面の方程式に代入すると
\(\small{ \ t=\displaystyle\frac{6}{49} \ }\)
よって垂線の長さは
\(\small{ \ \displaystyle\frac{6}{49}\times \vert(6, \ 3, \ 2)\vert=\displaystyle\frac{6}{7} \ }\)
\(\small{ \ \triangle\mathrm{ABC} \ }\)の面積は
\(\small{ \ \overrightarrow{\mathrm{AB}}=(-2, \ 4, \ 0) \ }\)、\(\small{ \ \overrightarrow{\mathrm{AC}}=(0, \ 4, \ -6) \ }\)より
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
\left|\overrightarrow{\mathrm{AB}}\right|=\sqrt{2^2+4^2}=2\sqrt{5}\\
\left|\overrightarrow{\mathrm{AC}}\right|=\sqrt{4^2+(-6)^2}=2\sqrt{13}\\
\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}=16
\end{array}
\right.
\end{eqnarray} \ }\)
&=&14 \ \end{eqnarray}}\)
よって求める体積は
\(\small{\begin{eqnarray} \ \mathrm{V}&=&\displaystyle\frac{1}{3}\times14\times\displaystyle\frac{6}{7}\\
&=&4 \ \end{eqnarray}}\)

\(\small{ \ \left(
\begin{array}{c}
-2 \\
4 \\
0
\end{array}
\right)\times\left(
\begin{array}{c}
0 \\
4 \\
-6
\end{array}
\right)=\left(
\begin{array}{c}
-24 \\
-12 \\
-8
\end{array}
\right) \ }\)
これって平面の方程式から求めた法線ベクトル\(\small{ \ (6, \ 3, \ 2) \ }\)と平行なのが分かるよね。
外積は向きがあるから逆向きになっているけど、平面の方程式を求めてその係数から法線ベクトルを出してそれが合っているか調べるのに外積は十分役に立つからね。
それにこの外積の大きさは\(\small{ \ 2 \ }\)つのベクトルが作る平行四辺形の大きさに等しいから、外積の大きさを半分にした値が底面の三角形の面積になるからね。

