こんにちは、リンス(@Lins016)です。
今回は二次関数のグラフと平方完成について学習していこう。
二次関数のグラフと言えば平方完成
高校生の間で何度もする作業の中で、最も多いのが二次関数の平方完成。
中高一貫校だったら中学のときからやってるよね。これは出来て当たり前。だけど数学のテストは出来るだけじゃダメなんだよね。時間内に出来るってことが重要なんだ。だから平方完成もいつでも素早くできないといけない。
\(\small{ \ y=ax^2+bx+c \ }\)
\(\small{ \ \ \ =a\left(x^2+\displaystyle \frac{b}{a}x\right)+c \ }\)
\(\small{ \ \ \ =a\left\{\left(x+\displaystyle \frac{b}{2a}\right)^2-\left(\displaystyle \frac{b}{2a}\right)^2\right\}+c \ }\)
\(\small{ \ \ \ =a\left(x+\displaystyle \frac{b}{2a}\right)^2-\displaystyle \frac{b^2}{4a}+c \ }\)
\(\small{ \ \ \ =a\left(x+\displaystyle \frac{b}{2a}\right)^2-\displaystyle \frac{b^2-4ac}{4a} \ }\)
上の式の中括弧のある部分を飛ばして計算する方が早いんだけど、ミスする人はこの中括弧を飛ばしているせいでミスすることが多いから、ミスが多い人は中括弧をつけて必ず平方完成するようにしよう。
頭の中で計算して展開するより中括弧をつけた式を一つ多く書いた方が結局は早く計算できるからね。
一般形と標準形
二次関数は二つの式でよく表される。\(\small{ \ y=ax^2+bx+c \ }\)と\(\small{ \ y=a(x-p)^2+q \ }\)の形。
\(\small{ \ y=ax^2+bx+c \ }\)を一般形、\(\small{ \ y=a(x-p)^2+q \ }\)を標準形っていうから覚えておこう。
大抵の二次関数の問題文には一般形で式が与えられてることがほとんどだから、まずは標準形に変形するっていうのが流れだと思う。この一般形を標準形に変形することを平方完成っていうんだよね。じゃあなぜ標準形にするのか、そこら辺を詳しく考えていこう。
二次関数のグラフの頂点の座標と平方完成
なんで平方完成するのかっていうと、グラフの頂点を見つけるためなんだ。
グラフの頂点がわからないとグラフは書けないから頂点を見つけるために平方完成する。平方完成すると頂点の座標がわかるからグラフを書くことが出来るよね。\(\small{ \ y=a(x-p)^2+q \ }\)の頂点の座標は\(\small{ \ (p, \ q) \ }\)になるからね。
例えば\(\small{ \ a\gt0 \ }\)のとき\(\small{ \ a(x-p)^2 \ }\)は常に\(\small{ \ 0 \ }\)以上になるよね。ってことは\(\small{ \ y=a(x-p)^2+q \ }\)だから\(\small{ \ y\geqq q \ }\)になる。\(\small{ \ y=q \ }\)になるとき\(\small{ \ q=a(x-p)^2+q \ }\)より\(\small{ \ x=p \ }\)になる。
だから\(\small{ \ x=p \ }\)のとき最小値\(\small{ \ y=q \ }\)になってグラフの頂点の座標は\(\small{ \ (p, \ q) \ }\)になるんだ。
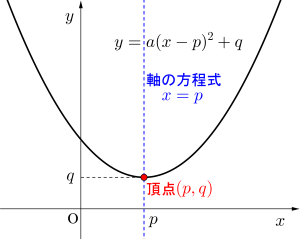
また\(\small{ \ x=p \ }\)を軸の方程式というから覚えておこう。
二次関数のグラフは放物線の形でこの軸に対して対称なグラフになるんだ。

グラフの凸に注意する
なんといっても二次関数で一番大切なのはグラフの凸の向きだよね。これで最大値や最小値が変わってくるからね。
\(\small{ \ y=ax^2+bx+c \ }\)や\(\small{ \ y=a(x-p)^2+q \ }\)のグラフは、\(\small{ \ a\gt0 \ }\)なら下に凸のグラフで頂点が一番下の点になり、\(\small{ \ a\lt0 \ }\)なら上に凸のグラフで頂点が一番上の点になる。
つまり\(\small{ \ x^2 \ }\)の係数の正負でグラフの凸の向きが変わるんだ。元から\(\small{ \ y=2x^2+3x+1 \ }\)のように\(\small{ \ x^2 \ }\)の係数が数字で与えられているグラフは問題ないけど、\(\small{ \ y=ax^2+3x+1 \ }\)のように数字じゃない文字の場合は正負での場合分けが必要だから注意しておこう。
次のグラフの頂点と軸の方程式を答え、グラフを図示せよ。
(1)\(\small{ \ y=\displaystyle \frac{1}{2}x^2-4x+3 \ }\)
(2)\(\small{ \ y=2(x-1)(x-4) \ }\)
(1)グラフを平方完成すると
\(\small{\begin{eqnarray} \ y&=&\displaystyle \frac{1}{2}x^2-4x+3\\
&=&\displaystyle \frac{1}{2}\left(x^2-8x\right)+3\\
&=&\displaystyle \frac{1}{2}\left\{\left(x-4\right)^2-4^2\right\}+3\\
&=&\displaystyle \frac{1}{2}\left(x-4\right)^2-5 \ \end{eqnarray}}\)
よって頂点の座標は\(\small{ \ \left(4, \ -5\right) \ }\)
軸の方程式は\(\small{ \ x=4 \ }\)
グラフは図のようになる。
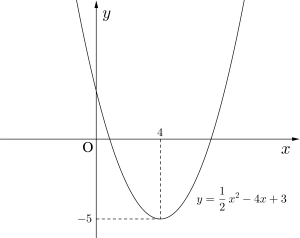
(2)グラフを平方完成すると
\(\small{\begin{eqnarray} \ y&=&2(x-1)(x-4)\\
&=&2\left(x^2-5x+4\right)\\
&=&2\left(x^2-5x\right)+8\\
&=&2\left\{\left(x-\displaystyle \frac{5}{2}\right)^2-\left(\displaystyle \frac{5}{2}\right)^2\right\}+8\\
&=&2\left(x-\displaystyle \frac{5}{2}\right)^2-\displaystyle \frac{9}{2} \ \end{eqnarray}}\)
よって頂点の座標は\(\small{ \ \left(\displaystyle \frac{5}{2}, \ -\displaystyle \frac{9}{2}\right) \ }\)
軸の方程式は\(\small{ \ x=\displaystyle \frac{5}{2} \ }\)
グラフは図のようになる。
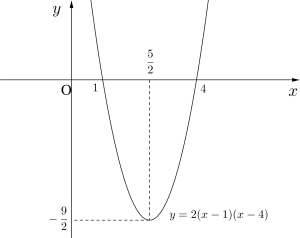

Point 二次関数のグラフと平方完成
①二次関数の頂点を調べるために式を平方完成する
②\(\small{ \ x^2 \ }\)の係数に注意して、必要なら傾きは正負の場合分け
\(\small{ \ y=ax^2+bx+c \ }\)のグラフが第\(\small{ \ 1 \ }\)象限に頂点を持ち、\(\small{\mathrm{A}(1, \ 0) \ }\)、\(\small{\mathrm{B}(-1, \ -2) \ }\)、\(\small{\mathrm{C}(0, \ 1) \ }\)とすると、\(\small{\mathrm{A} \ }\)、\(\small{\mathrm{B} \ }\)を通り、線分\(\small{ \ \mathrm{OC} \ }\)上の点\(\small{ \ \mathrm{D} \ }\)と交わるものとする。ただし、両端の点は含まない。このとき次の各値の符号を答えよ。
(1)\(\small{ \ a \ }\)
(2)\(\small{ \ b \ }\)
(3)\(\small{ \ c \ }\)
(4)\(\small{ \ a+b+c \ }\)
(1)第\(\small{ \ 1 \ }\)象限に頂点があり第\(\small{ \ 3 \ }\)象限の点\(\small{\mathrm{B}(-1, \ -2) \ }\)を通るので、グラフは下に凸のグラフ
よって\(\small{ \ a\lt0 \ }\)
(2)\(\small{\mathrm{A}(1, \ 0) \ }\)、\(\small{\mathrm{B}(-1, \ -2) \ }\)を通ることから頂点の\(\small{ \ x \ }\)座標は正の値になる。頂点の\(\small{ \ x \ }\)座標が正の値のとき\(\small{ \ a \ }\)と\(\small{ \ b \ }\)は異符号になるので\(\small{ \ b\gt0 \ }\)
(3)\(\small{ \ c \ }\)は\(\small{ \ y \ }\)切片の値になるので\(\small{ \ \mathrm{OC} \ }\)上の点\(\small{ \ \mathrm{D} \ }\)と交わることから\(\small{ \ c\gt0 \ }\)
(4)\(\small{ \ a+b+c \ }\)は\(\small{ \ x=1 \ }\)の\(\small{ \ y \ }\)座標を示すので、\(\small{\mathrm{A}(1, \ 0) \ }\)を通ることより\(\small{ \ a+b+c=0 \ }\)


