こんにちは、リンス(@Lins016)です。
今回は関数(グラフ)が固定され、定義域の一端が動く二次関数の最大最小について学習していこう。
二次関数の最大最小の場合分け問題
今回学習するのは関数が\(\small{ \ y=x^2-2x+3 \ }\)のように定められていて定義域が\(\small{ \ 0\leqq x \leqq a \ }\)のような定義域の一端に定数\(\small{ \ a \ }\)が入っているような二次関数の最大最小問題になる。
この形の問題は頂点の\(\small{ \ x \ }\)座標、つまりグラフの軸が固定されているから定義域に「グラフの軸を含まない」「グラフの軸を含んで固定端の方が他端よりグラフの軸から遠い」「グラフの軸を含んで固定端の方が他端よりグラフの軸に近い」で最大値や最小値をとる\(\small{ \ x \ }\)の値が変わってくるから、定義域とグラフの軸の位置関係によって定数\(\small{ \ a \ }\)の範囲を場合分けしていかないといけないんだ。
グラフと定義域をきちんと書いて練習していこう。
下に凸のグラフの場合
・定義域が(固定端)\(\small{\leqq x \leqq a \ }\)
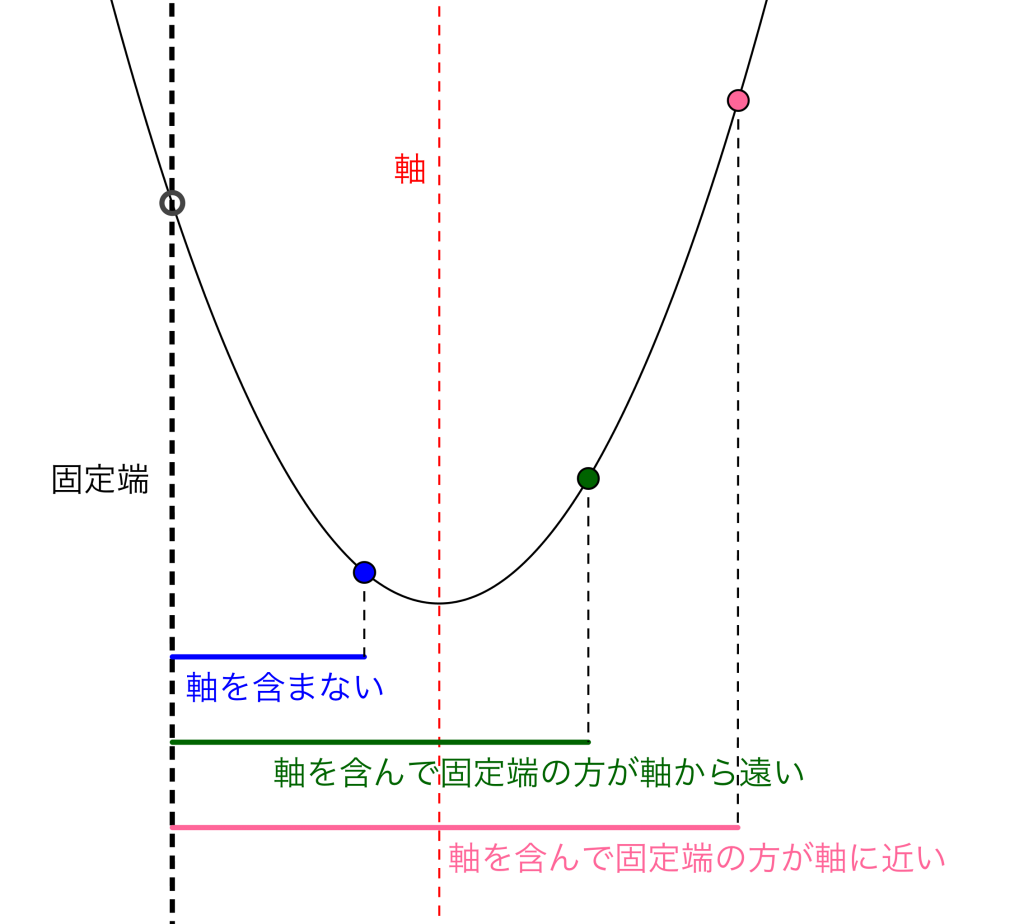
(i)軸を含まないとき
最大値\(\small{ \ f(固定端) \ }\)
最小値\(\small{ \ f(a) \ }\)
(ii)軸を含んで固定端の方が軸から遠いとき
最大値\(\small{ \ f(固定端) \ }\)
最小値\(\small{ \ f(軸) \ }\)
(iii)軸を含んで固定端の方が軸に近いとき
最大値\(\small{ \ f(a) \ }\)
最小値\(\small{ \ f(軸) \ }\)
定義域とグラフの軸の位置関係で場合分け
このタイプの問題は基本的に下の例題のように、固定端は軸を含んでいない場所にあるから、定義域の一端を移動させて最大最小をとる\(\small{ \ x \ }\) の値の変化を場合分けしていこう。
定義域に「軸を含まない」「軸を含んで固定端の方が軸から遠い」「軸を含んで固定端の方が軸に近い」の三つの場合から定数の範囲をきちんと場合分けして、最大値最小値を求めよう。
「軸を含んで固定端の方が軸から遠い」「軸を含んで固定端の方が軸に近い」の場合分けは軸が定義域の中央になる定数の値を求めて、それより大きいか小さいかで場合分けをしよう。
\(\small{ \ 0\leqq x \leqq a \ }\)における\(\small{ \ y=x^2-4x+5 \ }\)の最大値と最小値を求めよ。
まずは平方完成すると
\(\small{\begin{eqnarray}
y&=&x^2-4x+5\\
&=&(x-2)^2+1
\end{eqnarray}}\)
(i)\(\small{ \ a \lt 2 \ }\)のとき
グラフより
最大値\(\small{ \ x=0 \ }\)のとき\(\small{ \ 5 \ }\)
最小値\(\small{ \ x=a \ }\)のとき\(\small{ \ a^2-4a+5 \ }\)

(ii)\(\small{ \ 2 \leqq a \lt 4 \ }\)のとき
グラフより
最大値\(\small{ \ x=0 \ }\)のとき\(\small{ \ 5 \ }\)
最小値\(\small{ \ x=2 \ }\)のとき\(\small{ \ 1\ }\)

(iii)\(\small{ \ a \geqq 4 \ }\)のとき
グラフより
最大値\(\small{ \ x=a \ }\)のとき\(\small{ \ a^2-4a+5 \ }\)
最小値\(\small{ \ x=2 \ }\)のとき\(\small{ \ 1\ }\)
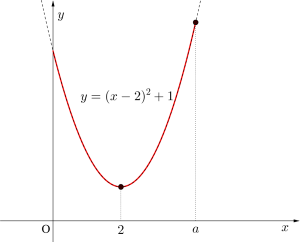

定義域と軸の位置によって最大や最小をとる\(\small{ \ x \ }\)の値が変化するから、各パターンの図を書いて最大値最小値を求めよう。
Point 二次関数の最大最小(グラフが固定で定義域の一端が動く)
①「軸を含まない」「軸を含んで固定端の方が軸から遠い」「軸を含んで固定端の方が軸に近い」に場合分けして最大値最小値を求める

