三角比の方程式と不等式（二次式への変形）

\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)のとき次の方程式、不等式を解け。
(1)\(\small{ \ 4\sin^2 \theta -4\cos \theta-1=0 \ }\)
(2)\(\small{ \ 2\cos^2\theta+3\sin \theta -3\geqq 0 \ }\)
(3)\(\small{ \ \sqrt{3}\tan^2 \theta +(\sqrt{3}-1)\tan \theta -1\leqq 0 \ }\)

(1)\(\small{ \ 4\sin^2 \theta -4\cos \theta-1=0 \ }\)
\(\small{ \ 4(1-\cos^2 \theta)-4\cos \theta -1=0 \ }\)
\(\small{ \ 4\cos^2 \theta +4\cos \theta -3=0 \ }\)
\(\small{ \ (2\cos \theta-1)(2\cos\theta+3)=0 \ }\)
\(\small{ \ \cos \theta =\displaystyle \frac{1}{2}, \ -\displaystyle \frac{3}{2} \ }\)
\(\small{ \ -1 \leqq \cos \theta \leqq 1 \ }\)より
\(\small{ \ \cos \theta =\displaystyle \frac{1}{2} \ }\)
\(\small{ \ \therefore \theta =60^{\circ} \ }\)

(2)\(\small{ \ 2\cos^2\theta+3\sin \theta -3\geqq 0 \ }\)
\(\small{ \ 2(1-\sin^2 \theta)+3\sin\theta-3\geqq 0 \ }\)
\(\small{ \ 2\sin^2\theta-3\sin\theta+1\leqq 0 \ }\)
\(\small{ \ (2\sin\theta-1)(\sin\theta-1)\leqq0 \ }\)
\(\small{ \ \displaystyle \frac{1}{2}\leqq \sin \theta \leqq 1 \ }\)
\(\small{ \ 30^{\circ}\leqq \theta \leqq 150^{\circ} \ }\)

(3)\(\small{ \ \sqrt{3}\tan^2 \theta+ (\sqrt{3}-1)\tan \theta -1\leqq 0 \ }\)
\(\small{ \ (\tan \theta +1)(\sqrt{3}\tan \theta-1)\leqq 0 \ }\)
\(\small{ \ -1\leqq \tan \theta \leqq \displaystyle \frac{1}{\sqrt{3}} \ }\)
\(\small{ \ 0^{\circ}\leqq \theta \leqq 30^{\circ}, \ 135^{\circ}\leqq \theta \leqq 180^{\circ} \ }\)

\(\small{ \ 2\sin^2x-\sin x-a=0 \ }\)の解を判別せよ。

\(\small{ \ 2\sin^2x-\sin x=a \ }\)
\(\small{ \ \sin x=t \ }\)とすると\(\small{ \ (0\leqq t \leqq 1) \ }\)
\(\small{ \ 2t^2-t=a \ }\)より
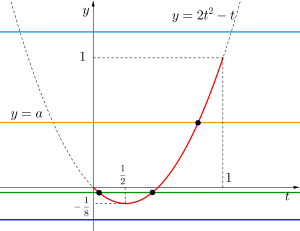
\(\small{ \ 　y=2t^2-t(0\leqq t \leqq 1) \ }\)と\(\small{ \ y=a \ }\)の交点の数について考える
\(\small{\begin{eqnarray} \ y&=&2t^2-t\\
&=&2\left(t-\displaystyle \frac{1}{4}\right)^2-\displaystyle \frac{1}{8} \ \end{eqnarray}}\)

よってグラフより
\(\small{ \ x \ }\)は\(\small{ \ 0 \leqq \sin x \lt 1  \ }\)の範囲で解を二つ持つことに注意すると
\(\small{ \ a \gt 1 \ }\)のとき解なし
\(\small{ \ a=1 \ }\)のとき解\(\small{ \ 1 \ }\)個
\(\small{ \ 0 \lt a \lt 1 \ }\)のとき解\(\small{ \ 2 \ }\)個
\(\small{ \ -\displaystyle\frac{1}{8} \lt a \leqq 0  \ }\)のとき解\(\small{ \ 4 \ }\)個
\(\small{ \ a=-\displaystyle\frac{1}{8} \ }\)のとき解\(\small{ \ 2 \ }\)個
\(\small{ \ a \lt -\displaystyle\frac{1}{8} \ }\)のとき解なし

\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)で\(\small{ \ \sin\theta+\cos\theta=\displaystyle\frac{1}{2} \ }\)のとき、\(\small{ \ \tan\theta\ }\)の値を求めよ。

\(\small{ \ \sin\theta+\cos\theta=\displaystyle\frac{1}{2} \ }\)より
\(\small{ \ \cos\theta=\displaystyle\frac{1}{2}-\sin\theta \ }\)を\(\small{ \ \sin^2 \theta+\cos^2 \theta=1 \ }\)に代入して
\(\small{ \ \sin^2 \theta+\left(\displaystyle\frac{1}{2}-\sin\theta \right)^2=1 \ }\)
これを整理して
\(\small{ \ 8\sin^2 \theta-4\sin\theta-3=0 \ }\)
\(\small{ \ \sin\theta=\displaystyle\frac{1\pm\sqrt{7}}{4} \ }\)
\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)から\(\small{ \ \sin\theta \geqq 0 \ }\)より
\(\small{ \ \sin\theta=\displaystyle\frac{1+\sqrt{7}}{4} \ }\)
\(\small{ \ \cos\theta=\displaystyle\frac{1}{2}-\sin\theta=\displaystyle\frac{1-\sqrt{7}}{4} \ }\)
よって\(\small{ \ \tan\theta=\displaystyle\frac{\displaystyle\frac{1+\sqrt{7}}{4}}{\displaystyle\frac{1-\sqrt{7}}{4}}=-\displaystyle\frac{4+\sqrt{7}}{3} \ }\)

\(\small{ \ \sin\theta+\cos\theta=\displaystyle\frac{1}{2} \ }\)より、両辺\(\small{ \ 2 \ }\)乗すると
\(\small{ \ \left(\sin\theta＋\cos\theta\right)^2=\left(\displaystyle\frac{1}{2}\right)^2 \ }\)
\(\small{ \ 1+2\sin\theta\cos\theta=\displaystyle\frac{1}{4} \ }\)
\(\small{ \ \sin\theta\cos\theta=-\displaystyle\frac{3}{8} \ }\)
ここで解と係数の関係を用いると
\(\small{ \ t^2-\displaystyle\frac{1}{2}t-\displaystyle\frac{3}{8}=0 \ }\)の解は\(\small{ \ \sin\theta \ }\)と\(\small{ \ \cos\theta \ }\)になるので、これを解くと
\(\small{ \ 8t^2-4t-3=0 \ }\)
\(\small{ \ t=\displaystyle\frac{1\pm\sqrt{7}}{4} \ }\)
\(\small{ \ 0^{\circ} \leqq \theta \leqq 180^{\circ} \ }\)と\(\small{ \ \sin\theta\cos\theta=-\displaystyle\frac{3}{8} \ }\)より
\(\small{ \ \sin\theta=\displaystyle\frac{1+\sqrt{7}}{4} \ }\)、\(\small{ \ \cos\theta=\displaystyle\frac{1-\sqrt{7}}{4} \ }\)
よって\(\small{ \ \tan\theta=\displaystyle\frac{\displaystyle\frac{1+\sqrt{7}}{4}}{\displaystyle\frac{1-\sqrt{7}}{4}}=-\displaystyle\frac{4+\sqrt{7}}{3} \ }\)