こんにちは、リンス(@Lins016)です。
今回は絶対値を含む関数について学習していこう。
絶対値とは?
絶対値とは原点からの距離を表したもので、\(\small{ \ |a| \ }\)のように数字を絶対値記号(縦棒)で数を囲むことで表すことができる。
この値は原点からの距離を示すから常に\(\small{ \ 0 \ }\)以上で\(\small{ \ | \ 5 \ |=5, \ |-3 \ |=3 \ }\)ってなる。
これは絶対値記号の中が正の数か\(\small{ \ 0 \ }\)のときは絶対値記号をそのまま外し、絶対値記号の中が負の数のときはマイナスをつけて絶対値記号を外すことで常にその値を正の数にすることができるんだ。
\(\small{ \ |x|=\pm \ x \ }\)ってする人がいるけど、\(\small{ \ x\geqq0 \ }\)のとき、\(\small{ \ |x|=x \ }\)、\(\small{ \ x\lt 0 \ }\)のとき、\(\small{ \ |x|=-x \ }\)になるから注意しよう。
\(\small{ \ \begin{eqnarray}
| x |
=
\begin{cases}
x & ( x \geqq 0 ) \\
-x & ( x \lt 0 )
\end{cases}
\end{eqnarray} \ }\)
絶対値は必ず場合分けをして絶対値記号を外そう
絶対値記号をそのままにした状態で問題を解いていくことなんてないから、必ず絶対値記号の中が\(\small{ \ 0 \ }\)以上の場合と負の場合に範囲を場合分けをして問題を解こう。
絶対値記号の中が二次関数の場合も同じで、絶対値記号の中の二次関数が\(\small{ \ 0 \ }\)以上と負の場合の範囲を求めて場合分けしないといけない。
\(\small{ \ |ax^2+bx+c| \ }\)は\(\small{ \ ax^2+bx+c\geqq0 \ }\)を満たす範囲のとき\(\small{ \ ax^2+bx+c \ }\)に、\(\small{ \ ax^2+bx+c\leqq0 \ }\)を満たす範囲のとき\(\small{ \ -ax^2-bx-c \ }\)になる。
だからまずは絶対値記号の中が\(\small{ \ 0 \ }\)以上や負になる範囲を二次不等式を解いて求めよう。
二次不等式の求め方を忘れている人はもう一度確認しておこう。
-

二次不等式の解き方
2次不等式の解き方について学習します。数字だけのものから定数を含んだ不等式について解説しています。
続きを見る
次の関数のグラフを図示せよ。
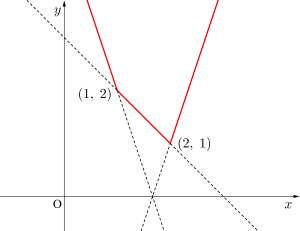
(1)\(\small{ \ y=|x-1|+|2x-4| \ }\)
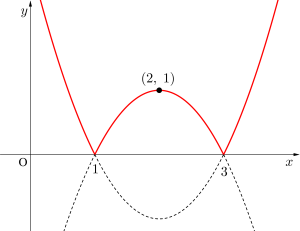
(2)\(\small{ \ y=|x^2-4x+3| \ }\)
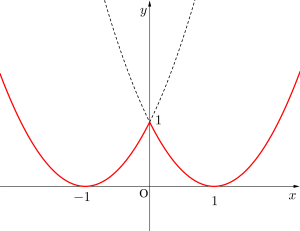
(3)\(\small{ \ y=x^2-2|x|+1 \ }\)
(1)
\(\small{ \ \begin{eqnarray}
| x-1 |
=
\begin{cases}
x-1 & ( x \geqq 1 ) \\
-x+1 & ( x \lt 1 )
\end{cases}
\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}
| 2x-4 |
=
\begin{cases}
2x-4 & ( x \geqq 2 ) \\
-2x+4 & ( x \lt 2 )
\end{cases}
\end{eqnarray} \ }\)
よってこれらをまとめると
\(\small{ \ \begin{eqnarray}
y
=
\begin{cases}
-3x+5 & ( x \lt 1 ) \\
-x+3 & ( 1\leqq x \lt 2 )\\
3x-5 & (x\geqq 2)
\end{cases}
\end{eqnarray} \ }\)
(2)
\(\small{ \ | x^2-4x+3 |\\
=
\begin{cases}
x^2-4x+3 & ( x \leqq 1, \ x\geqq3 ) \\
-x^2+4x-3 & ( 1 \lt x \lt 3 )
\end{cases} \ }\)
(3)
\(\small{ \ \begin{eqnarray}
| x |
=
\begin{cases}
x & ( x \geqq 0 ) \\
-x & ( x \lt 0 )
\end{cases}
\end{eqnarray} \ }\)
\(\small{ \ \begin{eqnarray}
y
=
\begin{cases}
x^2-2x+1 & ( x \geqq 0 ) \\
x^2+2x+1 & ( x \lt 0 )
\end{cases}
\end{eqnarray} \ }\)

Point 絶対値を含む関数のグラフ
①絶対値は絶対値記号の中を正負の範囲に分けて絶対値記号を外そう
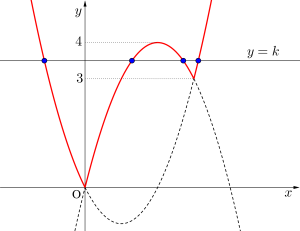
方程式\(\small{ \ |x^2-3x|=-x+k \ }\)の解が\(\small{ \ 4 \ }\)個になるとき、定数\(\small{ \ k \ }\)の値の範囲を求めよ。
\(\small{ \ |x^2-3x|=-x+k \ }\)
\(\small{ \ |x^2-3x|+x=k \ }\)
これを満たす\(\small{ \ x \ }\)の異なる解の個数は
\(\small{\begin{eqnarray}
\left\{
\begin{array}{l}
y=|x^2-3x|+x\\
y=k
\end{array}
\right.
\end{eqnarray} \ }\)
の交点の個数と一致する
\(\small{ \ \begin{eqnarray}
y
=
\begin{cases}
x^2-2x & ( x \leqq 0, \ x\geqq 3 ) \\
-x^2+4x & ( 0\lt x \lt 3 )
\end{cases}
\end{eqnarray} \ }\)
よってグラフより
\(\small{ \ 3\lt k \lt 4 \ }\)

定数が\(\small{ \ x \ }\)の係数にじゃない問題は、この定数を分離する方法を覚えておこう。
\(\small{ \ x \ }\)の係数に定数がある場合は使えないけど、\(\small{ \ x \ }\)の係数じゃなかったら、定数を分離することで答えを簡単に求めることができるからね。


