三角関数の最大最小（二次関数への変形）

こんにちは、リンス(@Lins016)です。
今回は三角関数の最大最小（二次関数への変換）について学習していこう。

三角関数の最大値と最小値

三角関数の最大値と最小値を求める問題は複数あるけど、その中で一番よく出題されるものに二次関数への変形がある。

っていっても二次関数への変換も複数のパターンがあるから今回は各パターンについてしっかりと学習していこう。

置換する三角関数と定義域

三角関数を二次関数に変換する場合、\(\small{ \ t=\sin x \ }\)や\(\small{ \ t=\sin x+\cos x \ }\)とおいて\(\small{ \ t \ }\)を変数とする二次関数の最大最小問題として解くんだ。

このとき注意しないといけないのが、\(\small{ \ t \ }\)には範囲が存在するってこと。

\(\small{ \ x \ }\)に範囲がなくても\(\small{ \ -1\leqq \sin x \leqq 1 \ }\)になるから、\(\small{ \ -1 \leqq t \leqq 1 \ }\)になるよね。

だから三角関数を\(\small{ \ t \ }\)と置換する場合、必ず範囲を考える必要があるから注意しよう。

\(\small{ \ \sin^2 x+\cos^2 x=1 \ }\)を利用する二次関数

\(\small{ \ y=\sin^2 x+\cos x +2 \ }\)のような\(\small{ \ \sin^2x \ }\)や\(\small{ \ \cos^2x \ }\)と\(\small{ \ \sin x \ }\)や\(\small{ \ \cos x \ }\)の一次の項を含む最大最小を求める問題は一次の項を\(\small{ \ t \ }\)とおいて\(\small{ \ t \ }\)の二次関数にしよう。

このとき\(\small{ \ \sin^2 x=1-\cos^2 x \ }\)になるから\(\small{ \ y=\sin^2 x+\cos x +2 \ }\)は、\(\small{ \ y=-t^2+t+3 \ }\)
になるよね。

これは一次の項を\(\small{ \ t \ }\)と置換すれば、二次の項は\(\small{ \ \sin^2 x+\cos^2 x=1 \ }\)が常に成り立つから、\(\small{ \ \sin x \ }\)や\(\small{ \ \cos x \ }\)どちらでも表すことができるよね。

だから常に一次の項を\(\small{ \ t \ }\)とおいて問題を解こう。このとき\(\small{ \ t \ }\)の範囲を求めるのを忘れないようにね。

\(\small{ \ \tan x \ }\)を置換する二次関数

\(\small{ \ \tan x \ }\)を\(\small{ \ t \ }\)と置換する場合、\(\small{ \ t \ }\)の範囲に注意しよう。

\(\small{ \ \sin x \ }\)や\(\small{ \ \cos x \ }\)と違って\(\small{ \ \tan x \ }\)は\(\small{ \ x \ }\)に制限する範囲がなかったら\(\small{ \ \tan x \ }\)は\(\small{ \ -\infty \ }\)から\(\small{ \ \infty \ }\)まで取りうるからね。

\(\small{ \ \cos2x \ }\)を含む三角関数の二次関数への置換

次は\(\small{ \ \cos2x \ }\)を含む\(\small{ \ y=\cos2x+\cos x+3 \ }\)のような問題について考えてみよう。

二倍角の公式を加法定理を利用して覚えている人は\(\small{ \ \cos2x=\cos^2x-\sin^2x \ }\)って覚えていると思うけど、実際この公式はさほど利用しない。

だって\(\small{ \ \cos^2x-\sin^2x \ }\)はどちらも二次に項だから\(\small{ \ \sin^2 x+\cos^2 x=1 \ }\)が成り立つことを考えると\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の両方使ってるのっておかしいよね。

だから二倍角の公式は\(\small{ \ \cos2x=1-2\sin^2x \ }\)か\(\small{ \ \cos2x=2\cos^2x-1 \ }\)として覚えておこう。

つまり\(\small{ \ \cos2x \ }\)は一次の項を\(\small{ \ t \ }\)とおけば\(\small{ \ t \ }\)の二次式で表すことができるから\(\small{ \ y=\cos2x+\cos x+3 \ }\)は\(\small{ \ y=2t^2+t+2 \ }\)って変形することができるよね。

一次の項が\(\small{ \ \sin x \ }\)の\(\small{ \ y=\cos2x+\sin x+3 \ }\)の場合は\(\small{ \ t=\sin x \ }\)として\(\small{ \ y=-2t^2+t+4 \ }\)になる。

つまり\(\small{ \ \cos2x \ }\)を\(\small{ \ \sin x \ }\)か\(\small{ \ \cos x \ }\)のどっちで表すかっていうのは一次の項で判断しよう。

あとはさっきまでと同じで\(\small{ \ t \ }\)の範囲に注意して問題を解こう。

\(\small{ \ \sin x+\cos x \ }\)を置換する二次関数

このタイプが一番よく入試でも出題されるパターンで\(\small{ \ t=\sin x+\cos x \ }\)や\(\small{ \ t=\sqrt{3}\sin x +\cos x \ }\)のように\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の和を\(\small{ \ t \ }\)って置換して二次関数にする問題なんだ。

例えば\(\small{ \ t=\sin x+\cos x \ }\)とすると\(\small{ \ t^2=(\sin x+\cos x)^2=1+2\sin x\cos x \ }\)になるから\(\small{ \ \sin x\cos x \ }\)を\(\small{ \ t \ }\)の二次式で表すことができる。
つまり\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の和を\(\small{ \ t \ }\)って置換すると、\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の積を\(\small{ \ t \ }\)の二次式で表すことができるんだ。

また\(\small{ \ \sin2x=2\sin x\cos x \ }\)だから\(\small{ \ \sin2x \ }\)も\(\small{ \ t \ }\)の二次式で表すことができるからね。

ただ問題を見て何を\(\small{ \ t \ }\)っておけばいいかわかりにくいんだけど、大体の場合は「\(\small{ \ t=\sin x+\cos x \ }\)とする」みたいに問題文に与えられていることが多い。

だけど、何を\(\small{ \ t \ }\)っておけばいいか書いていない場合もあるから、最大最小を求める問題で\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の和と\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の積が式にあったら\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の和を\(\small{ \ t \ }\)っておいてみよう。

このことから\(\small{ \ y=2\sin x \cos x+\sin x +\cos x +3 \ }\)は\(\small{ \ y=t^2+t+2 \ }\)に、\(\small{ \ y=\sin 2x+\sin x +\cos x +3 \ }\)も\(\small{ \ y=t^2+t+2 \ }\)に置換することができるんだ。

ただ\(\small{ \ t \ }\)の二次関数にできたからって終わりじゃないからね。
このとき重要になるのが\(\small{ \ t \ }\)の範囲。

\(\small{ \ t=\sin x+\cos x \ }\)のとき、合成を利用して\(\small{ \ t=\sin x+\cos x=\sqrt{2}\sin\left(x+\displaystyle\frac{\pi}{4}\right) \ }\)ってなるから\(\small{ \ 0 \leqq x \lt 2\pi \ }\)なら\(\small{ \ -\sqrt{2}\leqq t \leqq \sqrt{2} \ }\)になるからね。

\(\small{ \ \sin x \ }\)と\(\small{ \ \cos x \ }\)の偏角が同じ和や差は合成を利用するんだったよね。
三角関数の合成がまだ不完全な人は必ずできるようにしておこう。

二次関数の最大値と最小値

ここまで三角関数を二次関数に変換する方法について話してきたけど、重要なのはこのあと二次関数の最大最小問題として問題を解くことだよね。

三角関数に限らず、指数関数、対数関数も二次関数に置換して問題を解くことって多いから、まずは二次関数の最大最小問題を確実に解けるようにしておく必要がある。

だから二次関数の最大最小問題も必ずチェックしておこう。

問題解答

次の関数の最大値と最小値を求めよ。ただし\(\small{ \ 0\leqq x \lt 2\pi \ }\)とする。
(1)\(\small{ \ y=\cos^2x+\sin x+2 \ }\)
(2)\(\small{ \ y=\tan^2x+2\tan x+3 \ }\)
(3)\(\small{ \ y=\cos2x+2\sin x+1 \ }\)
(4)\(\small{ \ y=\sin x\cos x+\sin x+\cos x+2 \ }\)

(1)
\(\small{\begin{eqnarray} \ y&=&\cos^2x+\sin x+2\\
&=&1-\sin^2x+\sin x+2\\
&=&-\sin^2x+\sin x+3 \ \end{eqnarray}}\)
\(\small{ \ \sin x=t \ }\)とすると\(\small{ \ -1\leqq t \leqq 1 \ }\)
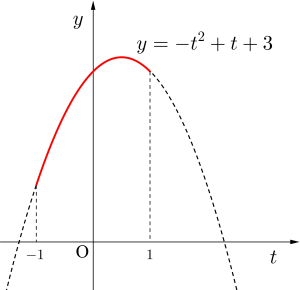
\(\small{\begin{eqnarray} \ y&=&-t^2+t+3\\
&=&-\left(t-\displaystyle\frac{1}{2}\right)^2+\displaystyle\frac{13}{4} \ \end{eqnarray}}\)
\(\small{ \ -1\leqq t \leqq 1 \ }\)より
最大になるのは\(\small{ \ t=\displaystyle\frac{1}{2} \ }\)のとき
最小になるのは\(\small{ \ t=-1 \ }\)のとき
最大値\(\small{ \ \displaystyle\frac{13}{4}\left(x=\displaystyle\frac{\pi}{6}, \ \displaystyle\frac{5}{6}\pi\right) \ }\)
最小値\(\small{ \ 1\left(x=\displaystyle\frac{3}{2}\pi\right) \ }\)

(2)
\(\small{ \ y=\tan^2x+2\tan x+3 \ }\)
\(\small{ \ t=\tan x \ }\)とすると\(\small{ \ t \ }\)は実数全体を動く
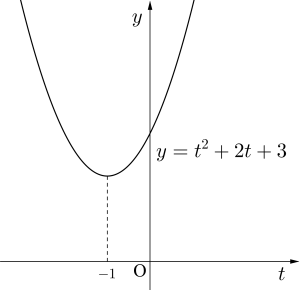
\(\small{\begin{eqnarray} \ y&=&t^2+2t+3\\
&=&\left(t+1\right)^2+2 \ \end{eqnarray}}\)
\(\small{ \ t \ }\)の範囲は実数全体より
最小になるのは\(\small{ \ t=-1 \ }\)のとき
最大値は存在しない
最大値なし
最小値\(\small{ \ 2\left(x=\displaystyle\frac{3}{4}\pi, \ \displaystyle\frac{7}{4}\pi\right) \ }\)

(3)
\(\small{\begin{eqnarray} \ y&=&\cos2x+2\sin x+1\\
&=&1-2\sin^2x+2\sin x+1\\
&=&-2\sin^2x+2\sin x+2 \ \end{eqnarray}}\)
\(\small{ \ \sin x=t \ }\)とすると\(\small{ \ -1\leqq t \leqq 1 \ }\)
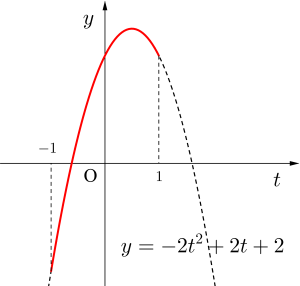
\(\small{\begin{eqnarray} \ y&=&-2t^2+2t+2\\
&=&-2\left(t-\displaystyle\frac{1}{2}\right)^2+\displaystyle\frac{5}{2} \ \end{eqnarray}}\)
\(\small{ \ -1\leqq t \leqq 1 \ }\)より
最大になるのは\(\small{ \ t=\displaystyle\frac{1}{2} \ }\)のとき
最小になるのは\(\small{ \ t=-1 \ }\)のとき
最大値\(\small{ \ \displaystyle\frac{5}{2}\left(x=\displaystyle\frac{\pi}{6}, \ \displaystyle\frac{5}{6}\pi\right) \ }\)
最小値\(\small{ \ -2\left(x=\displaystyle\frac{3}{2}\pi\right) \ }\)

(4)
\(\small{ \ y=\sin x\cos x+\sin x+\cos x +2 \ }\)
\(\small{ \ t=\sin x+\cos x \ }\)とすると\(\small{ \ t^2=1+2\sin x\cos x \ }\)
\(\small{\begin{eqnarray} \ y&=&\sin x\cos x+\sin x+\cos x+2\\
&=&\displaystyle\frac{t^2-1}{2}+t+2\\
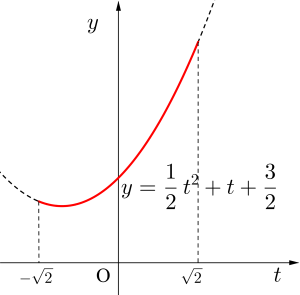
&=&\displaystyle\frac{t^2}{2}+t+\displaystyle\frac{3}{2}\\
&=&\displaystyle\frac{1}{2}\left(t+1\right)^2+1 \ \end{eqnarray}}\)
\(\small{ \ t=\sqrt{2}\sin\left(x+\displaystyle\frac{\pi}{4}\right) \ }\)より
\(\small{ \ -\sqrt{2}\leqq t \leqq \sqrt{2} \ }\)
最大になるのは\(\small{ \ t=\sqrt{2} \ }\)のとき
最小になるのは\(\small{ \ t=-1 \ }\)のとき
最大値\(\small{ \ \displaystyle\frac{5}{2}+\sqrt{2}\left(x=\displaystyle\frac{\pi}{4}\right) \ }\)
最小値\(\small{ \ 1\left(x=\pi, \ \displaystyle\frac{3}{2}\pi\right) \ }\)

実際試験に出題される場合(4)は\(\small{ \ t=\sin x+\cos x \ }\)っておくように誘導があると思うけど、誘導がなくても解けるようにしておこう。

Point　三角関数の合成

①加法定理を利用した合成をマスターしよう
②図形を利用した\(\small{ \ \sin \ }\)型の合成をマスターしよう

問題解答

次の関数について各問いに答えよ。

\(\small{ \ f(x)=a\left(\sqrt{3}\sin x+\cos x\right)+\sin x\left(\sin x+\sqrt{3}\cos x\right) \ }\)

ただし、\(\small{ \ 0\leqq x \leqq \pi \ }\)とする。
(1)\(\small{ \ t=\sqrt{3}\sin x+\cos x \ }\)として\(\small{ \ f(x) \ }\)を\(\small{ \ t \ }\)で表せ。
(2)\(\small{ \ f(x) \ }\)の最小値を求めよ。

(1)
\(\small{ \ t=\sqrt{3}\sin x+\cos x \ }\)より
\(\small{\begin{eqnarray} \ t^2&=&3\sin^2x+2\sqrt{3}\sin x\cos x+\cos^2x\\
&=&2\sin^2x+2\sqrt{3}\sin x\cos x+1 \ \end{eqnarray}}\)
\(\small{ \ \sin x\left(\sin x+\sqrt{3}\cos x\right)=\displaystyle\frac{t^2-1}{2} \ }\)
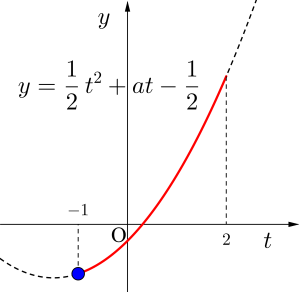
\(\small{ \ f(x)=\displaystyle\frac{t^2}{2}+at-\displaystyle\frac{1}{2} \ }\)

(2)
\(\small{ \ y=\displaystyle\frac{1}{2}t^2+at-\displaystyle\frac{1}{2} \ }\)とする
ここで
\(\small{\begin{eqnarray} \ t&=&\sqrt{3}\sin x+\cos x\\
&=&2\sin\left(x+\displaystyle\frac{\pi}{6}\right) \ \end{eqnarray}}\)
\(\small{ \ 0\leqq x \leqq \pi \ }\)より\(\small{ \ -1\leqq t \leqq 2 \ }\)
\(\small{\begin{eqnarray} \ y&=&\displaystyle\frac{1}{2}t^2+at-\displaystyle\frac{1}{2}\\
&=&\displaystyle\frac{1}{2}\left(t+a\right)^2-\displaystyle\frac{1}{2}a^2-\displaystyle\frac{1}{2} \ \end{eqnarray}}\)

(i)\(\small{ \ -a\lt -1\ }\)のとき
\(\small{ \ \therefore a\gt1 \ }\)のとき
\(\small{ \ t=-1 \ }\)のとき最小になる
最小値\(\small{ \ -a \ }\)

(ii)\(\small{ \ -1 \leqq -a\leqq 2\ }\)のとき
\(\small{ \ \therefore -2 \leqq a \leqq 1 \ }\)のとき
\(\small{ \ t=a \ }\)のとき最小になる
最小値\(\small{ \ -\displaystyle\frac{1}{2}a^2-\displaystyle\frac{1}{2} \ }\)

(iii)\(\small{ \ -a\gt 2\ }\)のとき
\(\small{ \ \therefore a\lt-2 \ }\)のとき
\(\small{ \ t=2 \ }\)のとき最小になる
最小値\(\small{ \ 2a+\displaystyle\frac{3}{2} \ }\)

三角関数を二次関数に変換するとき定義域が存在することがほとんどだから、関数に\(\small{ \ a \ }\)のような定数が含まれているとグラフの軸と定義域の位置関係で場合分けが必要になるから注意しよう。