こんにちは、リンス(@Lins016)です。
今回は分割した四面体の体積の求め方について学習していこう。
分割された四面体の体積の求め方
前回四面体の体積の求め方を学習したけど、今回はその四面体を分割した体積を求めていこう。
求め方は分割した立体の底面積の大きさや高さを直接求めるわけじゃなくて、元の四面体に対して底面積や高さがどんな比になっているか調べて、その値から体積比を求めて体積を求めていくんだ。
四面体を底面や高さが求めやすいように回転
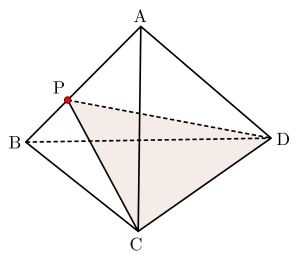
\(\small{ \ 2 \ }\)つの頂点を通る平面で分割した四面体
図のように四面体\(\small{ \ \mathrm{ABCD} \ }\)の\(\small{ \ \mathrm{AB} \ }\)上に点\(\small{ \ \mathrm{P} \ }\)を取り、この点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{C}, \ \mathrm{D} \ }\)を通る平面で分割した体積を求めてみよう。

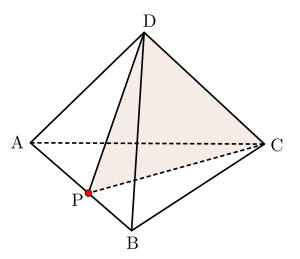
この\(\small{ \ 2 \ }\)つの頂点を通る平面で分割した四面体の場合、上の図だと体積を求めにくいから、四面体を回転させてみよう。
四面体を回転させてみると、分割された\(\small{ \ 2 \ }\)つの立体は底面積が分割されただけで、高さは変わってないのが確認できるよね。

つまり元の体積を\(\small{ \ \triangle\mathrm{APD}:\triangle\mathrm{BPD} \ }\)の比に分割することになるんだ。
\(\small{ \ \triangle\mathrm{APD}:\triangle\mathrm{BPD}=\mathrm{AP}:\mathrm{BP} \ }\)だから 四面体\(\small{ \ \mathrm{ABCD} \ }\)の体積を\(\small{ \ \mathrm{V} \ }\)とすると\(\small{ \ \displaystyle\frac{\mathrm{AP}}{\mathrm{AB}}\mathrm{V} \ }\)と\(\small{ \ \displaystyle\frac{\mathrm{BP}}{\mathrm{AB}}\mathrm{V} \ }\)に分割するってことだからね。
3辺の内分点を通る面で分割した四面体
次に\(\small{ \ 3 \ }\)辺を内分した点を通る平面で分割した四面体の体積を求めてみよう。
図のように\(\small{ \ \mathrm{AB}, \ \mathrm{AC}, \ \mathrm{AD} \ }\)をそれぞれ内分する点を\(\small{ \ \mathrm{P}, \ \mathrm{Q}, \ \mathrm{R} \ }\)として平面\(\small{ \ \mathrm{PQR} \ }\)で分割するってことね。
分割した立体のうち\(\small{ \ \mathrm{A} \ }\)を含む四面体の体積を考えてみよう。

この場合もそのまま体積を考えるのは難しいからまずは回転して考えてみよう。
今回は底面積だけじゃなくて高さも変わっているからそれぞれ考えないといけないからね。
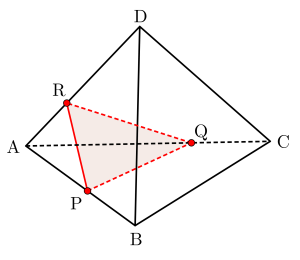
まずは底面について考えてみよう。
底面は\(\small{ \triangle \mathrm{APQ} \ }\)の面積\(\small{ \ \mathrm{S’} \ }\)は
\(\small{ \ \mathrm{S’}=\displaystyle\frac{1}{2}\mathrm{AP}\cdot\mathrm{AQ}\sin \mathrm{A} \ }\)
これは\(\small{ \triangle \mathrm{ABC} \ }\)の面積\(\small{ \ \mathrm{S} \ }\)と比較すると
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\mathrm{AB}\cdot\mathrm{AC}\sin \mathrm{A} \ }\)だから
\(\small{ \ \mathrm{S’}=\displaystyle\frac{\mathrm{AP}}{\mathrm{AB}}\cdot \displaystyle\frac{\mathrm{AQ}}{\mathrm{AC}}\mathrm{S} \ }\)
次に高さを考えてみよう。
図のように底面を平面\(\small{ \ \mathrm{ABC} \ }\)として、点\(\small{ \ \mathrm{D} \ }\)から平面に下ろした垂線の足を\(\small{ \ \mathrm{G} \ }\)とすると四面体\(\small{ \ \mathrm{ABCD} \ }\)の高さは\(\small{ \ \mathrm{DG} \ }\)になる。
同様に点\(\small{ \ \mathrm{R} \ }\)から平面に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)とすると四面体\(\small{ \ \mathrm{APQR} \ }\)の高さは\(\small{ \ \mathrm{RH} \ }\)になる。
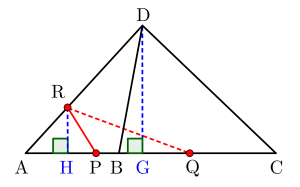
この図から\(\small{ \ \triangle \mathrm{ARH} \ }\)と\(\small{ \ \triangle\mathrm{ADG} \ }\)は相似だから\(\small{ \ \mathrm{RH:DG=AR:AD} \ }\)
つまり\(\small{ \ \mathrm{DG}=h \ }\)とすると\(\small{ \ \mathrm{RH}=\displaystyle\frac{\mathrm{AR}}{\mathrm{AD}}h \ }\)になる。
だから四面体\(\small{ \ \mathrm{ABCD} \ }\)の体積を\(\small{ \ \mathrm{V} \ }\)とすると\(\small{ \ \mathrm{V}=\displaystyle\frac{1}{3}\times \mathrm{S}\times h \ }\)
\(\small{ \ \mathrm{APQR} \ }\)の体積を\(\small{ \ \mathrm{V'} \ }\)とすると
\(\small{\begin{eqnarray} \ \mathrm{V}&=&\displaystyle\frac{1}{3}\times \mathrm{S'}\times \mathrm{RH}\\[6pt]
&=&\displaystyle\frac{1}{3}\times\displaystyle\frac{\mathrm{AP}}{\mathrm{AB}}\cdot \displaystyle\frac{\mathrm{AQ}}{\mathrm{AC}}\mathrm{S}\times\displaystyle\frac{\mathrm{AR}}{\mathrm{AD}}h\\[6pt]
&=&\displaystyle\frac{\mathrm{AP}}{\mathrm{AB}}\cdot \displaystyle\frac{\mathrm{AQ}}{\mathrm{AC}}\cdot\displaystyle\frac{\mathrm{AR}}{\mathrm{AD}}\mathrm{V} \ \end{eqnarray}}\)
になる。
つまりこれは体積が各辺の内分の比をかけたものになってるってことを表してるよね。

回転させない状態のままで考えられなくもないけど、回転させたほうがわかりやすいよね。どちらの場合も線分を内分した比の値が体積に影響しているってのがわかったからね。
もちろんこの考え方を使わずに直接分割する平面に垂線を下ろして垂線の長さや分割する平面の面積を求めてもいい。
だけど計算がすごく大変だから内分の値を使って比で計算するほうが楽だから、この方法で計算するようにしよう。
もちろん分割前の四面体の体積も求められないといけないから、そっちも復習しておこう。
Point 分割した四面体の体積の求め方
①体積を求めやすい底面を定める
②分割前の体積と底面積や高さがどう変化したのか比を求める

