こんにちは、リンス(@Lins016)です。今回は常用対数を利用した桁数問題(完全版)について学習していこう。
桁数・小数第何位・最高位の数・下一桁の数
常用対数を利用する問題といえば桁数を求める問題がある。桁数問題は桁数を求める問題に合わせて最高位の数や上から二桁目の数、下一桁の数とか求める問題があるから、その解き方まで確実に押さえておこう。
\(\small{ \ 10^p\lt n \lt 10^{p+1} \ }\)のとき
\(\small{ \ p\lt \log_{10}n \lt p+1 \ }\)
\(\small{ \ n \ }\)は\(\small{ \ p+1 \ }\)桁
\(\small{ \ 10^{-(p+1)}\lt n \lt 10^{-p} \ }\)のとき
\(\small{ \ -(p+1)\lt \log_{10}n \lt -p \ }\)
\(\small{ \ n \ }\)は小数第\(\small{ \ p+1 \ }\)で初めて\(\small{ \ 0 \ }\)以外の数が現れる
桁数の求め方
桁数問題ではいつも常用対数を利用して考えよう。なんで常用対数を利用するかって言うと、底が\(\small{ \ 10 \ }\)の対数を利用することで桁数を簡単に計算することができるから。
だって僕らが桁数で使うのはだいたい\(\small{ \ 10 \ }\)進法だからね。底が\(\small{ \ 10 \ }\)の常用対数と相性がいいんだ。
\(\small{ \ 10\leqq n \lt 100 \ }\)を満たす整数\(\small{ \ n \ }\)は\(\small{ \ 2 \ }\)桁の数だよね。
\(\small{ \ 100\leqq n \lt 1000 \ }\)を満たす整数\(\small{ \ n \ }\)なら\(\small{ \ 3 \ }\)桁の数になる。
この不等式を常用対数にしてみると
\(\small{ \ 10\leqq n \lt 100 \ }\)は\(\small{ \ \log_{10}10\leqq \log_{10}n \lt \log_{10}100 \ }\)
\(\small{ \ \therefore1\lt \log_{10}n \lt 2 \ }\)
\(\small{ \ 100\leqq n \lt 1000 \ }\)なら\(\small{ \ \log_{10}100\leqq \log_{10}n \lt \log_{10}1000 \ }\)
\(\small{ \ \therefore2\leqq \log_{10}n \lt 3 \ }\)
桁数を求めたい数の常用対数をとって、その値がどんな整数の間にあるか調べれば桁数を求めることができるんだ。
一般的に\(\small{ \ p\leqq \log_{10}n \lt p+1 \ }\)なら\(\small{ \ 10^p\leqq n \lt 10^{p+1} \ }\)になって\(\small{ \ n \ }\)は\(\small{ \ p+1 \ }\)桁の数になる。
ちなみに桁数問題では常用対数を利用するから\(\small{ \ \log_{10}2=0.301 \ }\)や\(\small{ \ \log_{10}3=0.4771 \ }\)が与えられてることが多い。
この値を利用して\(\small{ \ 5^{50} \ }\)の桁数について考えてみよう。
\(\small{\begin{eqnarray} \ \log_{10}5^{50}&=&50\log_{10}5\\
&=&50\times0.6990\\
&=&34.95 \ \end{eqnarray}}\)
つまり\(\small{ \ 34\lt \log_{10}5^{50}\lt35 \ }\)
\(\small{ \ 34\log_{10}10\lt \log_{10}5^{50}\lt35\log_{10} \ }\)
\(\small{ \ \log_{10}10^{34}\lt \log_{10}5^{50}\lt\log_{10}10^{35} \ }\)
\(\small{ \ \therefore 10^{34}\lt5^{50}\lt 10^{35} \ }\)
だから\(\small{ \ 5^{50} \ }\)は\(\small{ \ 35 \ }\)桁の整数になるんだ。
最高位の数の求め方
次に\(\small{ \ 5^{50} \ }\)の最高位の数について求めてみよう。
\(\small{ \ \log_{10}5^{50}=34.95 \ }\)だからこれを変形して\(\small{ \ 5^{50}=10^{34.95} \ }\)ってかけるよね。

\(\small{ \ 34.95 \ }\)の部分を整数部分と小数部分に分けると\(\small{ \ 5^{50}=10^{0.95}\times10^{34} \ }\)ってなるよね。
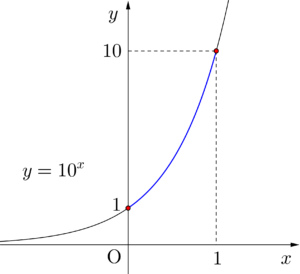
ここで指数関数\(\small{ \ y=10^x \ }\)のグラフを考えると、\(\small{ \ 10^0=1 \ }\)で\(\small{ \ 10^1=10 \ }\)だから\(\small{ \ 0\lt x\lt 1 \ }\)のとき\(\small{ \ 1\lt10^x \lt10 \ }\)だよね。
つまり小数部分をとった\(\small{ \ 10^{0.95} \ }\)は\(\small{ \ 10 \ }\)より小さい数ってことになるよね。
物理や化学を学習したことがある人は\(\small{ \ 1.52\times10^3 \ }\)といった有効数字を利用するような書き方って見たことあると思うけど、これって\(\small{ \ 1 \ }\)桁の整数+小数を\(\small{ \ 10^n \ }\)倍するって記述の方法で\(\small{ \ 1.52\times10^3=1520 \ }\)になって\(\small{ \ 4 \ }\)桁の数になる。\(\small{ \ 1.52\times10^5 \ }\)なら\(\small{ \ 1.52\times10^5=152000 \ }\)ってなって\(\small{ \ 6 \ }\)桁の数になる。
\(\small{ \ 1 \ }\)桁の整数+小数部分を\(\small{ \ a \ }\)とすると\(\small{ \ a\times10^{p} \ }\)は\(\small{ \ p+1 \ }\)桁の数になるんだ。
\(\small{ \ 10^{0.95}\times10^{34} \ }\)もその書き方になっていて\(\small{ \ 1 \ }\)桁の整数+小数部分が\(\small{ \ 10^{0.95} \ }\)、それを\(\small{ \ 10^{34} \ }\)倍して\(\small{ \ 5^{50} \ }\)になる。\(\small{ \ 1 \ }\)桁の整数+小数部分を\(\small{ \ 10^{34} \ }\)倍するから\(\small{ \ 5^{50} \ }\)は\(\small{ \ 35 \ }\)桁の整数になるよね。
さぁここからが本題になるけど、\(\small{ \ 5^{50} \ }\)の最高位の数は\(\small{ \ 5^{50}=10^{0.95}\times10^{34} \ }\)から\(\small{ \ 10^{0.95} \ }\)の整数部分だよね。だから\(\small{ \ 10^{0.95} \ }\)がいくつなのか調べればいいんだけど、この値を調べるのにも常用対数を使うんだ。
\(\small{ \ \log_{10}10^{0.95}=0.95 \ }\)
ここで\(\small{ \ \log_{10}2=0.301 \ }\)と\(\small{ \ \log_{10}3=0.4771 \ }\)が与えられていたら、\(\small{ \ \log_{10}8=3\log_{10}2=0.903 \ }\)、\(\small{ \ \log_{10}9=2\log_{10}3=0.9542 \ }\)になるから
\(\small{ \ \log_{10}8\lt \log_{10}10^{0.95} \lt \log_{10}9 \ }\)
\(\small{ \ \therefore 8\lt 10^{0.95} \lt 9 \ }\)
これから\(\small{ \ 5^{50} \ }\)の最高位は\(\small{ \ 8 \ }\)って言えるんだ。
この考え方は\(\small{ \ \log_{10}2=0.301 \ }\)と\(\small{ \ \log_{10}3=0.4771 \ }\)が与えられているとき解ける方法でこの常用対数の値の求め方は次の記事で確認しておこう。
下一桁の数の求め方
\(\small{ \ 2^n \ }\)の下一桁の数について考えていくと
\(\small{ \ 2^1→2 \ }\)
\(\small{ \ 2^2→4 \ }\)
\(\small{ \ 2^3→8 \ }\)
\(\small{ \ 2^4→6 \ }\)
\(\small{ \ 2^5→2 \ }\)
\(\small{ \ 2^6→4 \ }\)
って\(\small{ \ 2, \ 4, \ 8, \ 6 \ }\)を繰り返していくんだ。
これって\(\small{ \ 2^n \ }\)だけじゃなくて下一桁が\(\small{ \ 2 \ }\)なら一緒だから\(\small{ \ 12^n \ }\)や\(\small{ \ 22^n \ }\)も\(\small{ \ 2, \ 4, \ 8, \ 6 \ }\)を繰り返していくんだ。
\(\small{ \ 3^n \ }\)の下一桁について考えていくと
\(\small{ \ 3^1→3 \ }\)
\(\small{ \ 3^2→9 \ }\)
\(\small{ \ 3^3→7 \ }\)
\(\small{ \ 3^4→1 \ }\)
\(\small{ \ 3^5→3 \ }\)
\(\small{ \ 3^6→9 \ }\)
って\(\small{ \ 3, \ 9, \ 7, \ 1 \ }\)を繰り返していくんだ。
これも\(\small{ \ 3^n \ }\)だけじゃなくて下一桁が\(\small{ \ 3 \ }\)なら一緒だから\(\small{ \ 13^n \ }\)や\(\small{ \ 23^n \ }\)も\(\small{ \ 3, \ 9, \ 7, \ 1 \ }\)を繰り返していくんだ。
\(\small{ \ 4^n \ }\)の下一桁について考えていくと
\(\small{ \ 4^1→4 \ }\)
\(\small{ \ 4^2→6 \ }\)
\(\small{ \ 4^3→4 \ }\)
\(\small{ \ 4^4→6 \ }\)
\(\small{ \ 4^5→4 \ }\)
\(\small{ \ 4^6→6 \ }\)
って\(\small{ \ 4, \ 6 \ }\)を繰り返していくんだ。
これも\(\small{ \ 4^n \ }\)だけじゃなくて下一桁が\(\small{ \ 4 \ }\)なら一緒だから\(\small{ \ 14^n \ }\)や\(\small{ \ 24^n \ }\)も\(\small{ \ 4, \ 6 \ }\)を繰り返していくんだ。
\(\small{ \ 2^n, \ 3^n, \ 4^n \ }\)だけ例に挙げたけど、下一桁問題はどの場合でも規則的に繰り返すから、繰り返して何番目の数になるかキチンと求めよう。
\(\small{ \ 18^{18} \ }\)について答えよ。
ただし、\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)とする。
(1)\(\small{ \ 18^{18} \ }\)は何桁の数か。
(2)\(\small{ \ 18^{18} \ }\)の最高位の数はいくつか。
(3)\(\small{ \ 18^{18} \ }\)の下一桁の数はいくつか。
(1)
\(\small{\begin{eqnarray} \ \log_{10}18^{18}&=&18\log_{10}18\\
&=&18(\log_{10}2+2\log_{10}3)\\
&=&18\times(0.3010+0.4771\times2)\\
&=&22.5936 \ \end{eqnarray}}\)
よって\(\small{ \ 22 \lt \log_{10}18^{18}\lt 23 \ }\)
\(\small{ \ \therefore 10^{22}\lt 18^{18} \lt10^{23} \ }\)
したがって\(\small{ \ 18^{18} \ }\)は\(\small{ \ 23 \ }\)桁の整数である。
(2)
\(\small{ \ \log_{10}18^{18}=22.5936 \ }\)
\(\small{\begin{eqnarray} \ 18^{18}&=&10^{22.5936}\\
&=&10^{0.5936}\times10^{22} \ \end{eqnarray}}\)
\(\small{ \ \log_{10}10^{0.5936}=0.5936 \ }\)
\(\small{ \ \log_{10}3\lt\log_{10}10^{0.5936}\lt\log_{10}4 \ }\)
\(\small{ \ 3\lt10^{0.5936}\lt4 \ }\)
よって最高位の数は\(\small{ \ 3 \ }\)である。
(3)
下一桁だけ考えると
\(\small{ \ 18^1→8 \ }\)
\(\small{ \ 18^2→4 \ }\)
\(\small{ \ 18^3→2 \ }\)
\(\small{ \ 18^4→6 \ }\)
\(\small{ \ 18^5→8 \ }\)
となって\(\small{ \ 8, \ 4, \ 2, \ 6 \ }\)を繰り返す。
よって\(\small{ \ 18^{18} \ }\)の下一桁は\(\small{ \ 4 \ }\)

\(\small{ \ 5^{208} \ }\)の最高位と最高位から\(\small{ \ 2 \ }\)番目の数を求めよ。
ただし、\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)とする。
\(\small{\begin{eqnarray} \ \log_{10}5^{208}&=&208\times0.6990\\&=&145.392 \ \end{eqnarray}}\)
\(\small{ \ 5^{208}=10^{0.392}\times10^{145} \ }\)
\(\small{ \ \log_{10}10^{0.392}=0.392 \ }\)
\(\small{ \ \log_{10}2\lt\log_{10}10^{0.392}\lt\log_{10}3 \ }\)
\(\small{ \ 2 \lt 10^{0.392} \lt 3\ }\)
よって最高位の数は\(\small{ \ 2 \ }\)
\(\small{\begin{eqnarray} \ 5^{208}&=&10^{0.392}\times10^{145}\\
&=&10^{1.392}\times10^{144} \ \end{eqnarray}}\)
\(\small{ \ \log_{10}10^{1.392}=1.392 \ }\)
\(\small{\begin{eqnarray} \ \log_{10}24&=&\log_{10}2^3+\log_{10}3\\
&=&0.3010\times3+0.4771\\
&=&1.3801 \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \log_{10}25&=&\log_{10}5^2\\
&=&0.6990\times2\\
&=&1. 398 \ \end{eqnarray}}\)
\(\small{ \ \log_{10}24\lt \log_{10}10^{1.392}\lt \log_{10}25 \ }\)
\(\small{ \ 24 \lt 10^{1.392} \lt 25 \ }\)
よって最高位から\(\small{ \ 2 \ }\)番目の数は\(\small{ \ 4 \ }\)

最高位から\(\small{ \ 2 \ }\)番目を求める問題も最高位を求める方法を応用すれば思いつくよね。常用対数表を使わずに求めるとなると結構計算が面倒だけどね。
上の解答では\(\small{ \ \log_{10}24 \ }\)と\(\small{ \ \log_{10}25 \ }\)をあっさり計算してるけど、本当は\(\small{ \ \log_{10}20 \ }\)から\(\small{ \ \log_{10}21 \ }\)、\(\small{ \ \log_{10}22 \ }\)って順番に調べていかないといけないからね。
でも\(\small{ \ \log_{10}2 \ }\)と\(\small{ \ \log_{10}3 \ }\)の値しか与えられていないから、きちんと計算出来るのは\(\small{ \ \log_{10}20 \ }\)、\(\small{ \ \log_{10}24 \ }\)、\(\small{ \ \log_{10}25 \ }\)、\(\small{ \ \log_{10}27 \ }\)ぐらいだけどね。
ちなみに常用対数表を使えばもっと簡単に求めることも出来るんだ。常用対数表を利用した解き方も考えてみよう。そうすることでもっと桁数問題を深く理解することができるからね。
常用対数表の見方についても「常用対数とその値」の記事でチェックしておこう。
小数第何位の数求め方
\(\small{ \ a^b \ }\)の\(\small{ \ a \ }\)が整数なら桁数問題だったけど\(\small{ \ 0\lt a \lt1 \ }\)なら\(\small{ \ a^b \ }\)が初めて\(\small{ \ 0 \ }\)じゃない数が現れるの小数第何位かっていう問題になる。
\(\small{ \ 0.01\lt n \lt 0.10 \ }\)を満たす小数\(\small{ \ n \ }\)の初めて\(\small{ \ 0 \ }\)じゃない数が現れるのは小数第\(\small{ \ 2 \ }\)位だよね。
\(\small{ \ 0.001\lt n \lt 0.010 \ }\)を満たす小数\(\small{ \ n \ }\)なら初めて\(\small{ \ 0 \ }\)じゃない数が現れるのは小数第\(\small{ \ 3 \ }\)位になる。
この不等式を常用対数にしてみると
\(\small{ \ 0.01\lt n \lt 0.10 \ }\)は\(\small{ \ \log_{10}10^{-2}\lt \log_{10}n \lt \log_{10}10^{-1} \ }\)
\(\small{ \ \therefore -2\lt \log_{10}n \lt -1 \ }\)
\(\small{ \ 0.001\lt n \lt 0.010 \ }\)なら\(\small{ \ \log_{10}10^{-3}\lt \log_{10}n \lt \log_{10}10^{-2} \ }\)
\(\small{ \ \therefore -3 \lt \log_{10}n \lt -2 \ }\)
初めて\(\small{ \ 0 \ }\)じゃない数が現れるの小数第何位か求めるには、常用対数をとって、その値がどんな負の整数の間にあるか調べれば求めることができるんだ。
一般的に\(\small{ \ -(p+1)\lt \log_{10}n \lt -p \ }\)なら\(\small{ \ 10^{-(p+1)}\lt n \lt 10^{-p} \ }\)になって\(\small{ \ n \ }\)の初めて\(\small{ \ 0 \ }\)じゃない数が現れるのは小数第\(\small{ \ p+1 \ }\)位になる。
ちなみに問題でも常用対数を利用するから桁数問題と同じで\(\small{ \ \log_{10}2=0.301 \ }\)や\(\small{ \ \log_{10}3=0.4771 \ }\)が与えられてることが多い。
この値を利用して\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^{50} \ }\)の桁数について考えてみよう。
\(\small{\begin{eqnarray} \ \log_{10}\left(\displaystyle\frac{1}{2}\right)^{50}&=&-50\log_{10}2\\&=&-50\times0.3010\\&=&-15.05 \ \end{eqnarray}}\)
つまり\(\small{ \ -16\lt \log_{10}\left(\displaystyle\frac{1}{2}\right)^{50} \lt-15 \ }\)
\(\small{ \ -16\log_{10}10\lt \log_{10}\left(\displaystyle\frac{1}{2}\right)^{50} \lt-15\log_{10}10 \ }\)
\(\small{ \ \log_{10}10^{-16}\lt \log_{10}\left(\displaystyle\frac{1}{2}\right)^{50}\lt\log_{10}10^{-15} \ }\)
\(\small{ \ \therefore 10^{-16}\lt \left(\displaystyle\frac{1}{2}\right)^{50} \lt 10^{-15} \ }\)
だから\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^{50} \ }\)の初めて\(\small{ \ 0 \ }\)じゃない数が現れるのは小数第\(\small{ \ 16 \ }\)位になる。
初めて現れる0以外の数字の求め方
これも桁数問題の最高位の数を求めるように解くんだけど、まったく同じではないから注意しておいてほしい。
\(\small{ \ \log_{10}\left(\displaystyle\frac{1}{2}\right)^{50}=-15.05 \ }\)だから\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^{50}=10^{-15.05} \ }\)になるよね。
これを\(\small{ \ 10^{-0.05}\times10^{-15} \ }\)ってやると失敗なんだ。
例えば\(\small{ \ 10^a=2.\cdots \ }\)つまり\(\small{ \ 2\leqq 10^a \lt 3 \ }\)って数だったとするよね。
\(\small{ \ 10^{-a}=\displaystyle\frac{1}{2.\cdots} \ }\)ってなる。これっていくつかな?
\(\small{ \ \displaystyle\frac{1}{2} \ }\)なら\(\small{ \ 0.5 \ }\)、\(\small{ \ \displaystyle\frac{1}{2.5} \ }\)なら\(\small{ \ 0.4 \ }\)、\(\small{ \ \displaystyle\frac{1}{2.8} \ }\)なら\(\small{ \ 0.35\cdots \ }\)ってなるから、\(\small{ \ 0 \ }\)以外の初めて現れる数が\(\small{ \ 3, 4, \ 5 \ }\)のどれかはっきりしない。
だから\(\small{ \ 10^{-15.05} \ }\)は\(\small{ \ 10^{-0.05}\times10^{-15} \ }\)じゃなくて\(\small{ \ 10^{0.95}\times10^{-16} \ }\)って書くようにしよう。
これで\(\small{ \ 1 \ }\)桁の整数+小数を\(\small{ \ 10^{-16} \ }\)倍した値ってことになるから、\(\small{ \ 0 \ }\)じゃない最初の数は\(\small{ \ 10^{0.95} \ }\)を考えたらいいよね。
これは桁数の最高位を考える問題と同じになるから
\(\small{ \ \log_{10}10^{0.95}=0.95 \ }\)
ここで\(\small{ \ \log_{10}2=0.301 \ }\)と\(\small{ \ \log_{10}3=0.4771 \ }\)が与えられていたら、\(\small{ \ \log_{10}8=3\log_{10}2=0.903 \ }\)、\(\small{ \ \log_{10}9=2\log_{10}3=0.9542 \ }\)になるから
\(\small{ \ \log_{10}8\lt \log_{10}10^{0.95} \lt \log_{10}9 \ }\)
\(\small{ \ \therefore 8\lt 10^{0.95} \lt 9 \ }\)
これから\(\small{ \ \left(\displaystyle\frac{1}{2}\right)^{50} \ }\)の初めて\(\small{ \ 0 \ }\)以外の現れる数は\(\small{ \ 8 \ }\)って言えるんだ。
\(\small{ \ \left(\displaystyle\frac{1}{30}\right)^{20} \ }\)を小数で表したとき、小数第何位に初めて\(\small{ \ 0 \ }\)でない数字が現れるか。また、その初めて現れた数字はいくつか。
ただし、\(\small{ \ \log_{10}2=0.3010, \ \log_{10}3=0.4771 \ }\)とする。
\(\small{\begin{eqnarray} \ \log_{10}\left(\displaystyle\frac{1}{30}\right)^{20}&=&\log_{10}30^{-20}\\
&=&-20\log_{10}30\\
&=&-20\left(\log_{10}3+\log_{10}10\right)\\
&=&-20(0.4771+1)\\
&=&-29.542 \ \end{eqnarray}}\)
よって\(\small{ \ -30 \lt \log_{10}\left(\displaystyle\frac{1}{30}\right)^{20}\lt -29 \ }\)
\(\small{ \ \therefore 10^{-30}\lt \left(\displaystyle\frac{1}{30}\right)^{20} \lt 10^{-29} \ }\)
したがって\(\small{ \ \left(\displaystyle\frac{1}{30}\right)^{20} \ }\)は小数第\(\small{ \ 30 \ }\)位で初めて\(\small{ \ 0 \ }\)でない数字が現れる。
\(\small{\begin{eqnarray} \ \left(\displaystyle\frac{1}{30}\right)^{20}&=&10^{-29.542}\\
&=&0^{0.458}\times10^{-30} \ \end{eqnarray}}\)
\(\small{ \ \log_{10}10^{0.458}=0.458 \ }\)
\(\small{ \ \log_{10}2\lt\log_{10}10^{0.458}\lt\log_{10}3 \ }\)
\(\small{ \ 2\lt10^{0.458}\lt3 \ }\)
よって初めて現れる数字は\(\small{ \ 2 \ }\)である。

Point 常用対数を利用した桁数問題(完全版)
①桁数問題は常用対数による不等式から桁数を求める
②最高位の数は常用対数から求めた値の小数部分を利用して求める
③下一桁は規則的な変化を求める
\(\small{ \ 2^n \ }\)(\(\small{ \ n \ }\)は\(\small{ \ 0 \ }\)以上の整数)の最高位の数を\(\small{ \ f(n) \ }\)とする。例えば\(\small{ \ f(2)=4 \ }\)、\(\small{ \ f(5)=3 \ }\)である。\(\small{ \ \log_{10}2=0.30103 \ }\)、\(\small{ \ \log_{10}3=0.47712 \ }\)とするとき、次の問いに答えよ。
(1)\(\small{ \ f(300) \ }\)を求めよ。
(2)\(\small{ \ 0\leqq n \leqq 300 \ }\)の範囲で\(\small{ \ f(n)=4 \ }\)を満たす整数\(\small{ \ n \ }\)はいくつあるか。
(1)
\(\small{\begin{eqnarray} \ \log_{10}2^{300}&=&300\log_{10}2\\
&=&300\times0.30103\\
&=&90.309 \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ 2^{300}&=&10^{90.309}\\
&=&10^{0.309}\times10^{90} \ \end{eqnarray}}\)
\(\small{ \ \log_{10}10^{0.309}=0.309 \ }\)
\(\small{ \ \log_{10}2\lt\log_{10}10^{0.309}\lt\log_{10}3 \ }\)
\(\small{ \ \therefore f(300)=2 \ }\)
(2)
最高位の数が\(\small{ \ 1 \ }\)の数を順次\(\small{ \ 2 \ }\)倍していくと最高位の数は
\(\small{ \ 1→2→4→8 \ }\)
\(\small{ \ 1→2→4→9 \ }\)
\(\small{ \ 1→2→5 \ }\)
\(\small{ \ 1→3→6 \ }\)
\(\small{ \ 1→3→7 \ }\)
と\(\small{ \ 5 \ }\)つのパターンで変化し、いずれも次は\(\small{ \ 1 \ }\)となる。
最高位の数が\(\small{ \ 4 \ }\)となるのは
\(\small{ \ 1→2→4→8 \ }\)
\(\small{ \ 1→2→4→9 \ }\)
のときだけである。
ここでこの\(\small{ \ 2 \ }\)つのパターンは
\(\small{ \ ①→2→4→8→①' \ }\)
\(\small{ \ ①→2→4→9→①' \ }\)
と変化し、\(\small{ \ ① \ }\)のときの数を\(\small{ \ a \ }\)桁とすると\(\small{ \ ①' \ }\)の数は\(\small{ \ a+1 \ }\)桁になる。
\(\small{ \ 2^{0}=1 \ }\)から順次\(\small{ \ 2 \ }\)倍して、最高位の数が\(\small{ \ 2 \ }\)である\(\small{ \ 91 \ }\)桁の\(\small{ \ 2^{300} \ }\)になるまでに各桁の数において最高位の数字が\(\small{ \ 1→2→4→8 \ }\)、\(\small{ \ 1→2→4→9 \ }\)と変化する回数を\(\small{ \ x \ }\)回とすると
\(\small{ \ 4x+3(90-x)+2=301 \ }\)
\(\small{ \ \therefore x=29 \ }\)


