こんにちは、リンス(@Lins016)です。
今回は無限級数について学習していこう。
無限級数
無限級数とは無限に続く数列の和のこと。
この数列が等比数列だったら無限等比級数だったけど、今回は色々な無限級数について考えていこう。
・無限級数
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\lim_{n\to \infty}S_n\\[3pt]
&=&\displaystyle\lim_{n\to \infty}\displaystyle\sum_{k=1}^n a_k\\[3pt]
&=&\displaystyle\sum_{k=1}^{\infty}a_k \ \end{eqnarray}}\)
・無限級数の収束
\(\small{ \ \displaystyle\lim_{n\to \infty} \mathrm{S}_n \ }\)が収束するとき\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)
ただし\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)でも\(\small{ \ \displaystyle\lim_{n\to \infty} \mathrm{S}_n \ }\)が収束するとは限らない。
総和と部分和
無限等比級数のときと同じで、すべての和(総和)を求めるためには、まず\(\small{ \ n \ }\)項目までの和(部分和)を求めて、そして部分和の極限から総和を求めるんだ。
\(\large{ \ \underbrace{\overbrace{ a_1 +a_2+ \cdots + a_n }^{部分和\mathrm{S}_n}+\cdots}_{総和\mathrm{S}} \ }\)
無限級数の極限の極限の求め方はこれが基本になるからね。
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\lim_{n\to \infty}\mathrm{S}_n\\[3pt]
&=&\displaystyle\lim_{n\to \infty}\displaystyle\sum_{k=1}^n a_k\\[3pt]
&=&\displaystyle\sum_{k=1}^{\infty}a_k \ \end{eqnarray}}\)
いろいろな数列の和
部分和を求めることって極限とは関係なくて、単に数列の和を求めることだよね。
数列の和といえば\(\small{ \ \displaystyle\sum \ }\)を利用することが多い。そのためにまず一般項\(\small{ \ a_n \ }\)を求めて、そして和を求めるっていうの基本だよね。
一般項がどんな形なのか、それによって和の求め方が変わってくるんだったよね。
①\(\small{ \ \displaystyle\sum \ }\)の公式がそのまま使える場合 Σの意味から使い方まで詳しく解説しています。 続きを見る
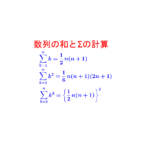
数列の和とΣの計算
②一般項が分数になる場合 部分分数分解を利用した数列の和について詳しく解説しています。 続きを見る

分数の数列の和
③差を利用して和を求める場合 根号を含む数列の和や階乗を含む数列の和について詳しく解説しています。 続きを見る

差を利用する数列の和の求め方
④初項に\(\small{ \ n \ }\)を含む数列の和 k項目を一般項として和を求める方法について詳しく解説しています。 続きを見る
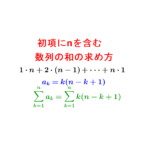
初項にnを含む数列の和の求め方
⑤等差数列×等比数列の和 和の求め方やΣ記号表記について詳しく解説しています。 続きを見る

等差数列と等比数列の積の和の求め方

次の無限級数の極限を調べよ。また、収束するときはその和を求めよ。
(1)
(2)
(3)
\(\small{ \ \displaystyle \sum_{ k= 1 }^{ \infty }(3k-2)x^{k-1}(0\lt x \lt1) \ }\)ただし、\(\small{ \ 0\lt x \lt1 \ }\)のとき\(\small{ \ \displaystyle\lim_{n\to \infty}nx^n=0 \ }\)である
(1)第\(\small{ \ n \ }\)項までの和を\(\small{ \ \mathrm{S}_n \ }\)とすると
よって求める和は
\(\small{ \ \displaystyle\lim_{n\to \infty}\mathrm{S}_n=\displaystyle \frac{5}{24} \ }\)
(2)
第\(\small{ \ n \ }\)項までの和を\(\small{ \ \mathrm{S}_n \ }\)とすると
よって求める和は
\(\small{ \ \displaystyle\lim_{n\to \infty}\mathrm{S}_n=\infty \ }\)
(3)\(\small{ \ \mathrm{S}_n=\displaystyle \sum_{ k = 1 }^{ n } (3k-2)x^{k-1} \ }\)とすると
-)x\mathrm{S}_n&=& & &\hspace{ 4pt }x+4x^2+\cdots&+&(3k-5)x^{n-1}&+&(3n-2)x^n\\
\hline
(1-x)\mathrm{S}_n&=&1&+&3x+3x^2+\cdots&+&3x^{n-1}&-&(3n-2)x^n\\
&=&1&+&\displaystyle \frac{3x(x^{n-1}-1)}{x-1}&-&(3n-2)x^n&&\end{eqnarray} }\)
よって
\(\small{ \ \displaystyle\lim_{n\to \infty}nx^n=0 \ }\)より
\(\small{ \ \displaystyle \sum_{ k = 1 }^{ \infty } (3k-2)x^{k-1}=\displaystyle \frac{1+2x}{(1-x)^2} \ }\)
無限級数が収束する条件
無限級数の和が収束する条件は、\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)じゃないといけないんだ。
例えば\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=2 \ }\)のとき、\(\small{ \ \displaystyle\lim_{n\to \infty}\displaystyle\sum_{k=1}^na_k \ }\)は、項数が大きくなると、ずっと\(\small{ \ 2 \ }\)が足される感じになるから無限大に発散するよね。
だから和が収束するなら\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)じゃないといけないんだ。
ただ、\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)だからと言って和が収束するわけじゃないから注意しよう。
例えば
\(\small{ \ 1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}}+\cdots \ }\)
について考えてみよう。
\(\small{ \ a_n=\displaystyle\frac{1}{\sqrt{n}} \ }\)だから\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)になるよね。
\(\small{ \ \mathrm{S}_n=1+\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{3}}+\cdots+\displaystyle\frac{1}{\sqrt{n}} \ }\)とすると\(\small{ \ 1\gt\displaystyle\frac{1}{\sqrt{2}}\gt\displaystyle\frac{1}{\sqrt{3}}\gt\cdots\gt\displaystyle\frac{1}{\sqrt{n}} \ }\)だから
が言えるよね。
右辺は\(\small{ \ n\cdot \displaystyle\frac{1}{\sqrt{n}}= \sqrt{n} \ }\)になる。
だから右辺の極限は
\(\small{ \ \displaystyle\lim_{n\to \infty}\sqrt{n}= \infty \ }\)になって、左辺は右辺より大きいから左辺の極限も無限大になるよね。
これは\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)のとき\(\small{ \ \displaystyle\lim_{n\to \infty}\mathrm{S}_n \ }\)は収束しなかったってことを示してるんだ。
つまり\(\small{ \ \displaystyle\lim_{n\to \infty} \mathrm{S}_n \ }\)が収束するなら、\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)が言えるけど、\(\small{ \ \displaystyle\lim_{n\to \infty}a_n=0 \ }\)だからといって、\(\small{ \ \displaystyle\lim_{n\to \infty} \mathrm{S}_n \ }\)が収束するとは言えないってこと。
とても大切なことだからしっかりと覚えておこう。
次の無限級数の極限を求めよ。
\(\small{ \ 1+\displaystyle\frac{3}{2}+\displaystyle\frac{5}{3}+\displaystyle\frac{7}{4}+\displaystyle\frac{9}{5}+\cdots \ }\)
第\(\small{ \ n \ }\)項を\(\small{ \ a_n \ }\)とすると
\(\small{ \ a_n= \displaystyle\frac{2n-1}{n} \ }\)
\(\small{\begin{eqnarray} \ \displaystyle\lim_{n\to \infty}a_n&=& \displaystyle\lim_{n\to \infty}\displaystyle\frac{2n-1}{n}\\
&=& \displaystyle\lim_{n\to \infty}\displaystyle\frac{2-\textstyle\frac{1}{n}}{1}\\
&=&2 \end{eqnarray} }\)
\(\small{ \ \displaystyle\lim_{n\to \infty}a_n\neq0 \ }\)より
\(\small{ \ 1+\displaystyle\frac{3}{2}+\displaystyle\frac{5}{3}+\displaystyle\frac{7}{4}+\displaystyle\frac{9}{5}+\cdots \ }\)は発散する

Point 無限級数
①部分和を求めてから総和を求める
②数列の和の求め方をマスターする
③和が収束する条件を覚える

