重複組み合わせ

こんにちは、リンス(@Lins016)です。
今回は重複組み合わせについて学習していこう。

重複組み合わせとは

\(\small{ \ n \ }\)種類のものの中から重複を許して\(\small{ \ r \ }\)個選ぶ組み合わせを重複組み合わせって言って、この総数を\(\small{ \ {}_n\mathrm{H}_r \ }\)って書くんだ。

重複組み合わせの利用

\(\small{ \ n \ }\)種類のものの中から重複を許して\(\small{ \ r \ }\)個選ぶ組み合わせって言われても、そんな風に出題されてる問題ってほとんどないよね。

どんな風に出題されているかっていうと、簡単な問題だと
「スーパーで果物を買うとき、みかん、りんご、なしを全部で\(\small{ \ 9 \ }\)個買うときの組み合わせはいくつあるか」
これだったらどうかな？

\(\small{ \ 3 \ }\)種類の中から重複を許して\(\small{ \ 9 \ }\)個選べばいいから\(\small{ \ {}_3\mathrm{H}_9 \ }\)になるよね。
ここで注意したいのが\(\small{ \ {}_3\mathrm{H}_9 \ }\)通りには、りんごだけ\(\small{ \ 9 \ }\)個買う場合も、みかん\(\small{ \ 6 \ }\)個とりんご\(\small{ \ 3 \ }\)個買う場合も入っているんだ。
買わないものがあってもいいってことね。

重複組み合わせ\(\small{ \ {}_n\mathrm{H}_r \ }\)の計算

この\(\small{ \ {}_n\mathrm{H}_r \ }\)が、どうして\(\small{ \ {}_{n+r-1}\mathrm{C}_r \ }\)になるのか考えてみよう。

一般化のまま考えるのは難しいから、さっきの「みかん、りんご、なしを全部で\(\small{ \ 9 \ }\)個買うときの組み合わせ\(\small{ \ {}_3\mathrm{H}_9 \ }\)」について考えてみよう。
全部で\(\small{ \ 9 \ }\)個あるから\(\small{ \ 9 \ }\)個の「○」と仕切り棒\(\small{ \ 2 \ }\)本「｜」を一列に並べてみよう。

一つ目の仕切り棒の左にあるものをみかん、二つの仕切り棒の間にあるものをりんご、二つ目の仕切り棒の右にあるものをなしとすると、この仕切り棒を\(\small{ \ 9 \ }\)個の「○」のどこに並べるか考えたら、全ての通りがでるよね。

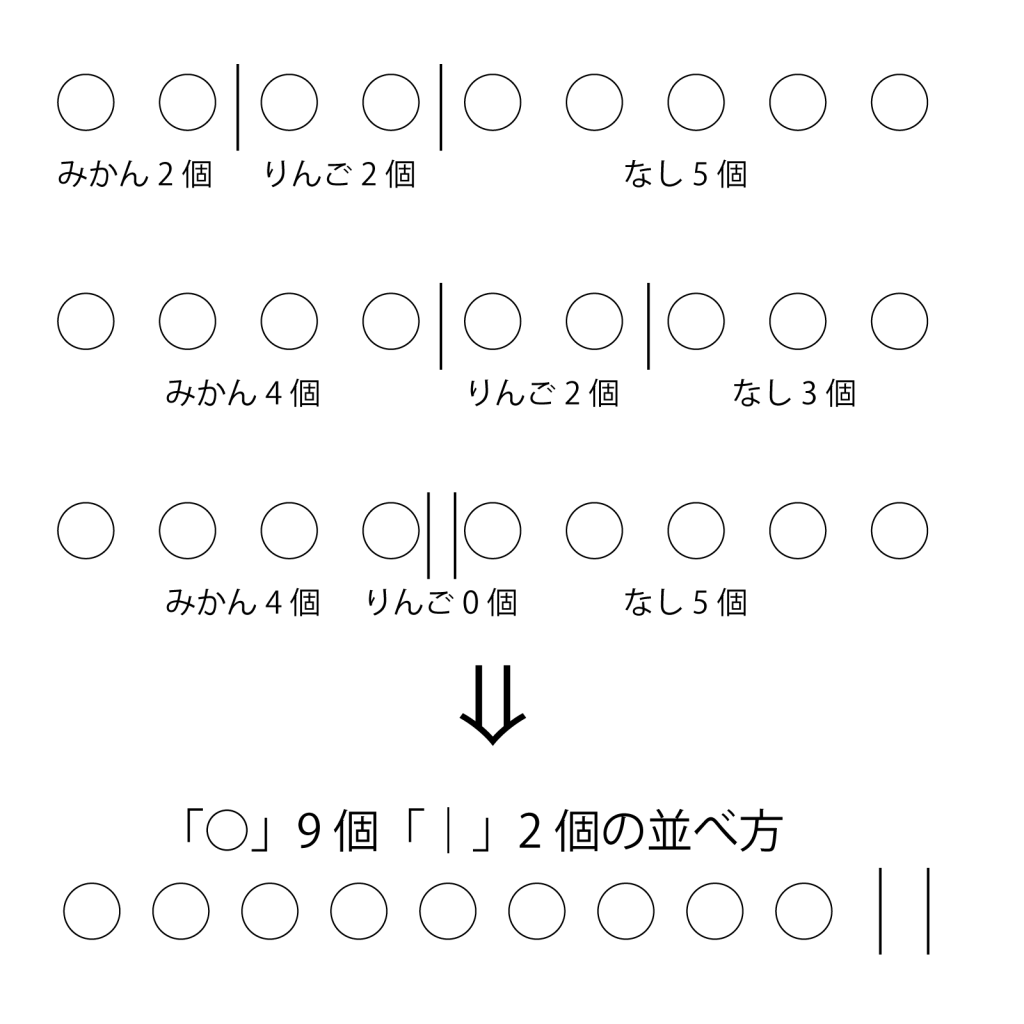
だから\(\small{ \ 9 \ }\)個の「○」と仕切り棒\(\small{ \ 2 \ }\)本「｜」を一列に並べた数が「みかん、りんご、なしを全部で\(\small{ \ 9 \ }\)個買うときの組み合わせ\(\small{ \ {}_3\mathrm{H}_9 \ }\)」になるんだ。
これって同じものを含む順列だから\(\small{ \ \displaystyle\frac{11!}{9!2!} \ }\)通りだよね。
つまり\(\small{ \ {}_{11}\mathrm{C}_9={}_{11}\mathrm{C}_2 \ }\)とも言えるよね。
\(\small{ \ {}_3\mathrm{H}_9={}_{11}\mathrm{C}_9 \ }\)になるんだ。

一般化して考えてみよう。
\(\small{ \ n \ }\)種類のものの中から重複を許して\(\small{ \ r \ }\)個選ぶってことは、「○」を\(\small{ \ r \ }\)個、「｜」は\(\small{ \ n \ }\)種類に分けたいんだから\(\small{ \ n-1 \ }\)本、これらすべてを一列に並べることを考えればいいよね。

だから「○」\(\small{ \ r \ }\)個と「｜」\(\small{ \ n-1 \ }\)本の並べ方は\(\small{ \ \displaystyle\frac{(n-1+r)!}{r!(n-1)!)}={}_{n+r-1}\mathrm{C}_r \ }\)通りになるんだ。

教科書には\(\small{ \ \mathrm{H} \ }\)のことについて記載されていないものも多いから、\(\small{ \ {}_n\mathrm{H}_r \ }\)より\(\small{ \ {}_{n+r-1}\mathrm{C}_r \ }\)として覚えておく方がいいかな。
どっちにしろ\(\small{ \ \mathrm{C} \ }\)じゃないと計算できないしね。

重複組み合わせと整数解・自然数解の個数

重複組み合わせの問題と言えば整数解の個数と自然数解の個数の問題があるからセットで覚えておこう。

その問題っていうのは、

の二つの問題。

最初の整数解の個数の問題はさっきのみかんとりんごとなしを\(\small{ \ 9 \ }\)個選ぶ問題と同じだよね。
だから、\(\small{ \ {}_3\mathrm{H}_9={}_{11}\mathrm{C}_9={}_{11}\mathrm{C}_2=55 \ }\)通りになるよね。

次の自然数解の個数の問題は、みかん、りんご、なしの問題に言い換えると「みかん、りんご、なしを全部で\(\small{ \ 9 \ }\)個選ぶうち、どれも最低\(\small{ \ 1 \ }\)個は選んで」ってことになるよね。

ってことはみかん、りんご、なしをあらかじめ\(\small{ \ 1 \ }\)個ずつ取っておいて、残り\(\small{ \ 6 \ }\)個を選ばないものがあってもいいってことで選べばいいよね。

あらかじめ\(\small{ \ 1 \ }\)個ずつ取っておくと考えると
\(\small{ \ (x-1)+(y-1)+(z-1)=9-3 \ }\)
ここで
\(\small{ \ X=x-1, \ Y=y-1, \ Z=z-1 \ }\)とすると
\(\small{ \ X+Y+Z=6, \ X\geqq0, \ Y\geqq0, \ Z\geqq0 \ }\)
これって残り\(\small{ \ 6 \ }\)個を選ばないものがあってもいいってことだよね。
ってことは
\(\small{ \ {}_3\mathrm{H}_6={}_{8}\mathrm{C}_6={}_{8}\mathrm{C}_2=28 \ }\)通りになるよね。

この\(\small{ \ x+y+z=r \ }\)、\(\small{ \ x\geqq0, \ y\geqq0, \ z\geqq0 \ }\)または\(\small{ \ x\gt0, \ y\gt0, \ z\gt0 \ }\)を満たす\(\small{ \ (x, \ y, \ z) \ }\)の整数解の組の個数、自然数の組の解の個数の問題は合わせて覚えておくようにしよう。

重複組み合わせHの意味

\(\small{ \ \mathrm{H} \ }\)は同次積の\(\small{ \ \mathrm{Homegenous \ Product} \ }\)の頭文字の\(\small{ \ \mathrm{H} \ }\)を意味しているんだ。
同次積って何？って思うかもしれないけど、次の問題を考えてみよう。

展開した一つの項を\(\small{ \ x^py^qz^r \ }\)とすると
\(\small{ \ p+q+r=5, \ p\geqq0, \ q\geqq0, \ r\geqq0 \ }\)になるから、展開式の異なる項の数は、
\(\small{ \ p+q+r=5, \ p\geqq0, \ q\geqq0, \ r\geqq0 \ }\)を満たす\(\small{ \ (p, \ q, \ r) \ }\)の整数の組の個数に等しいよね。
つまり項の数は\(\small{ \ {}_3\mathrm{H}_5={}_7\mathrm{C}_2=21 \ }\)通りになる。

この\(\small{ \ (x+y+z)^5 \ }\)のように同じ式をかけたものが同次積で、その展開式の項の数を重複組み合わせで求めることができるから、\(\small{ \ \mathrm{H} \ }\)は同次積\(\small{ \ \mathrm{Homegenous \ Product} \ }\)からきているんだ。

\(\small{ \ (x_1+x_2+\cdots+x_n)^r \ }\)の展開式の項の数は\(\small{ \ {}_n\mathrm{H}_r \ }\)になるからね。

重複組み合わせがどんな問題で利用できるか、\(\small{ \ \mathrm{H} \ }\)と\(\small{ \ \mathrm{C} \ }\)の関係とかポイントをきちんと押さえておこう！

Point　重複組み合わせ

①\(\small{ \ {}_n\mathrm{H}_r={}_{n+r-1}\mathrm{C}_r \ }\)
②整数解の個数、自然数解の個数を求めるときに利用する