複素数と図形（直線）

こんにちは、リンス(@Lins016)です。
今回は複素数と図形（直線）について学習していこう。

複素数平面上の図形

複素数平面も座標平面と同じようにある条件式を満たす図形、つまり軌跡の問題ってあるんだ。

「軌跡」って聞くとなんか嫌な感じがするかもしれないけど、条件式が何を示しているか理解していけば問題ない。

図形と方程式の軌跡だって同じで、いろんな形があるけど、どんな条件式ならどんな軌跡になるのかをきちんと考えて解けば、答えは必ず導けるからね。

方程式の表す図形

点\(\small{ \ \mathrm{P}\left(z\right) \ }\)の表す図形は\(\small{ \ z \ }\)を含む方程式が満たす点の集まりって考えることができるよね。

これが軌跡の考え方と同じなんだ。その上で複素数平面ではどんな方程式を書けば、どんな図形（軌跡）が描けるのか考える必要がある。

図形と方程式の軌跡っていうと直線、円、放物線だったよね。理系だとさらに楕円、双曲線が軌跡の答えに入ってくる。

今回は直線を表す方程式がどんな式なのか考えていこう。

座標平面だとどんな式になるか、複素数平面に合わせて考えてみると軌跡の復習にもなるから、確認しておこう。

直線を表す方程式

直線と言えば、\(\small{ \ 2 \ }\)点からの距離が等しい直線、つまり\(\small{ \ 2 \ }\)点を結ぶ線分の垂直二等分線。これが複素数平面では一番よく出題される直線になる。

複素数平面では点\(\small{ \ \mathrm{P}\left(z\right) \ }\)と点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)の距離は絶対値を利用して\(\small{ \ |z-\alpha| \ }\)って書くよね。

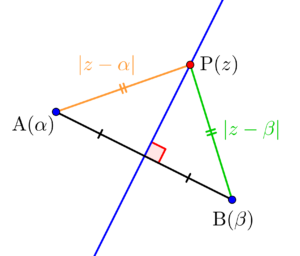
だから点\(\small{ \ \mathrm{A}\left(\alpha\right) \ }\)と点\(\small{ \ \mathrm{B}\left(\beta\right) \ }\)からの距離が等しい点\(\small{ \ \mathrm{P}\left(z\right) \ }\)は、
\(\small{ \ |z-\alpha|=|z-\beta| \ }\)
って書けるんだ。この点\(\small{ \ \mathrm{P}\left(z\right) \ }\)の集合が線分\(\small{ \ \mathrm{AB} \ }\)の垂直二等分線になるんだ。

だから\(\small{ \ |z-\alpha|=|z-\beta| \ }\)は線分\(\small{ \ \mathrm{AB} \ }\)の垂直二等分線を表す方程式になる。この形は確実に覚えておこう。

実軸に平行な直線の方程式

例えば実軸は\(\small{ \ i \ }\)、\(\small{ \ -i \ }\)の垂直二等分線って考えることができるから、実軸を表す方程式は\(\small{ \ |z-i|=|z+i| \ }\)って書くことができる。

でもこれ以外にも絶対値を利用せずに表す方程式もあるんだ。それは\(\small{ \ z-\overline{z}=0 \ }\)。\(\small{ \ z=x+yi \ }\)とすると\(\small{ \ z-\overline{z}=2y \ }\)になるから\(\small{ \ 2y=0 \ }\)から\(\small{ \ y=0 \ }\)。だから\(\small{ \ z \ }\)は実軸上にあるってことになるよね。

ちなみに\(\small{ \ z-\overline{z}=2i \ }\)なら\(\small{ \ y=1 \ }\)になるから、\(\small{ \ i \ }\)を通って実軸に平行な直線ってことになる。

だから「\(\small{ \ z-\overline{z}= \ }\)純虚数または\(\small{ \ 0 \ }\)」のとき、この方程式を満たす\(\small{ \ z \ }\)全体は実軸に平行な直線を描くことになるんだ。

ちなみに\(\small{ \ |z-i|=|z+i| \ }\)を整理すると
\(\small{ \ |z-i|^2=|z+i|^2 \ }\)
\(\small{ \ (z-i)\overline{(z-i)}=(z+i)\overline{(z+i)} \ }\)
\(\small{ \ (z-i)(\overline{z}+i)=(z+i)(\overline{z}-i) \ }\)
\(\small{ \ z\overline{z}+iz-i\overline{z}+1=z\overline{z}-iz+i\overline{z}+1 \ }\)
\(\small{ \ 2i(z-\overline{z})=0 \ }\)
\(\small{ \ \therefore z-\overline{z}=0 \ }\)
ってなって、絶対値を外した式を導くこともできるからね。

実軸に平行ってことは、虚軸に垂直ともいえるからね。逆に虚軸に平行なら実軸に垂直だよね。

虚軸に平行な直線の方程式

次に虚軸は\(\small{ \ 1 \ }\)、\(\small{ \ -1 \ }\)の垂直二等分線って考えることができるから、虚軸を表す方程式は\(\small{ \ |z-1|=|z+1| \ }\)って書くことができる。

でもこれも絶対値を利用しないで表すと\(\small{ \ z+\overline{z}=0 \ }\)になる。\(\small{ \ z=x+yi \ }\)とすると\(\small{ \ z+\overline{z}=2x \ }\)になるから\(\small{ \ 2x=0 \ }\)から\(\small{ \ x=0 \ }\)。だから\(\small{ \ z \ }\)は虚軸上にあるってことになるよね。

さっきの実軸に平行な場合と同じように、実部と虚部を入れ替えて考えたらいいよね。

ちなみに\(\small{ \ z+\overline{z}=2 \ }\)なら\(\small{ \ x=1 \ }\)になるから、\(\small{ \ 1 \ }\)を通って虚軸に平行な直線ってことになる。

だから「\(\small{ \ z+\overline{z}= \ }\)実数」のとき、この方程式を満たす\(\small{ \ z \ }\)全体は虚軸に平行な直線を描くことになる。

ちなみにさっきと同じように\(\small{ \ |z-1|=|z+1| \ }\)を整理すると
\(\small{ \ |z-1|^2=|z+1|^2 \ }\)
\(\small{ \ (z-1)\overline{(z-1)}=(z+1)\overline{(z+1)} \ }\)
\(\small{ \ (z-1)(\overline{z}-1)=(z+1)(\overline{z}+1) \ }\)
\(\small{ \ z\overline{z}-z-\overline{z}+1=z\overline{z}+z+\overline{z}+1 \ }\)
\(\small{ \ 2(z+\overline{z})=0 \ }\)
\(\small{ \ \therefore z+\overline{z}=0 \ }\)
って導くこともできるからね。

(2)は「\(\small{ \ 2 \ }\)点、\(\small{ \ 2-i \ }\)、\(\small{ \ 2+i \ }\)を結ぶ垂直二等分線」って答えたくなるけど、\(\small{ \ \alpha \ }\)と\(\small{ \ \overline{\alpha} \ }\)の垂直二等分線は実軸になるから注意しよう。\(\small{ \ 2-i \ }\)、\(\small{ \ 2+i \ }\)は共役だからね。

Point 複素数と図形（直線）

①\(\small{ \ |z-\alpha|=|z-\beta| \ }\)は垂直二等分線
②\(\small{ \ z-\overline{z}= \ }\)純虚数または\(\small{ \ 0 \ }\)は実軸に平行な直線
③\(\small{ \ z+\overline{z}= \ }\)実数は虚軸に平行な直線