こんにちは、リンス(@Lins016)です。
今回は常用対数表の利用について学習していこう。
常用対数表
常用対数って底が\(\small{ \ 10 \ }\)の対数のことだったよね。
底が\(\small{ \ 10 \ }\)の常用対数はよく使われることもあって、各値を調べて表にしてあるんだ。
このことについては以前の記事でも紹介したよね。
ちなみに常用対数表を作ったのは数学者ヘンリー・ブリッグスでwikipediaには次のように記されている。
数学者ヘンリー・ブリッグスが、ネイピアの対数を発案したジョン・ネイピアと議論をして、この定義のような改良を提案し常用対数表を作成したことによりブリッグスの対数とも呼ばれる。
あとこのあたりも参考になるかな。 続きを見る
対数の発見
常用対数と高校数学
高校の定期試験だと常用対数表を使う問題ってほとんど出題されない。
一応問題集には「常用対数表を使って\(\small{ \ \log_{10}314 \ }\)の値を求めよ。」みたいな問題はあるけど、実際の試験てなると、常用対数表を準備するの大変だから、\(\small{ \ \log_{10}2=0.3010 \ }\)と\(\small{ \ \log_{10}3=0.4771 \ }\)を与えとけば、定期試験の問題は作ることができるからね。
だから常用対数表を使って問題を解くことってほとんどなかったと思うんだけど、そうはいかなくなった。
なぜかというと京都大学の入試に常用対数表が与えられた桁数問題が出題されたんだ。
これ焦った先生も多いと思う。だって常用対数表の使い方や見方をきちんと教えてない先生って結構いるからね。(多分・・・。)
だから今回は常用対数表の見方や使い方について話したいと思う。
常用対数の基本問題
一般的な常用対数の問題といえば、常用対数のうち\(\small{ \ \log_{10}2=0.3010 \ }\)や\(\small{ \ \log_{10}3=0.4771 \ }\)の数値を近似で与えておいて、その数値を使えば解ける問題だった。
まずはこのパターンをきちんと理解しておこう。これきちんと出来てないと先に進めないからね。
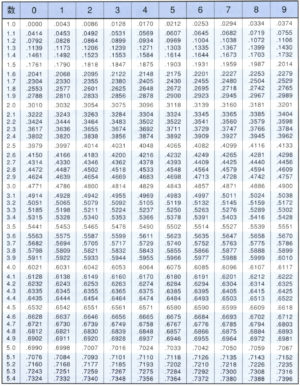
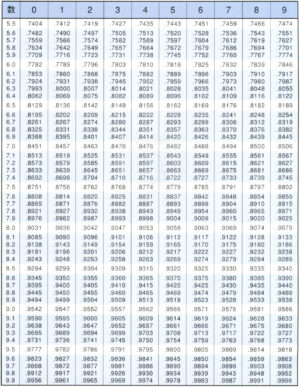
常用対数表の値
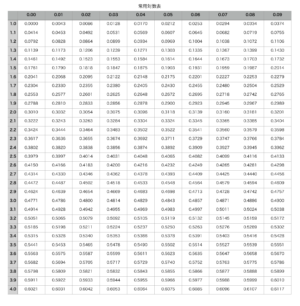
数学の教科書に記載されている常用対数表の値は、大抵の教科書で小数第4位まで載ってる。
\(\small{ \ \log_{10}(2.00) \ }\)の欄を見ると\(\small{ \ 0.3010 \ }\)になってるけど、\(\small{ \ \log_{10}(4.00) \ }\)は\(\small{ \ 0.6021 \ }\)になってるよね。
ん???\(\small{ \ \log_{10}(4.00)=0.6020 \ }\)じゃないの?って思ったよね。
この欄の数値がその対数の値だとすると\(\small{ \ \log_{10}4=2\log_{10}2 \ }\)が成り立たないことになるよね。
これだと対数の性質\(\small{ \ \log_ab^r=r\log_ab \ }\)と矛盾することになる。
でも実際は\(\small{ \ \log_{10}2=0.3010 \ }\)、\(\small{ \ \log_{10}4=0.6021 \ }\)じゃないんだ。
これはあくまで小数第\(\small{ \ 4 \ }\)位まで書いた時の値って話だから、小数第\(\small{ \ 5 \ }\)位で四捨五入してあるんだ。
だから小数第\(\small{ \ 4 \ }\)位まで記載されてる常用対数表からわかるのは
\(\small{ \ 0.30095\leqq \log_{10}2 \lt 0.30105 \ }\)
\(\small{ \ 0.60205\leqq \log_{10}4 \lt 0.60215 \ }\)
ってことなんだ。
もちろん他の値でも同じように、常用対数の値じゃなくて、範囲がわかるっていうのが正しい使い方だからね。
この考え方を利用して実際に出題された入試問題を解いてみよう。
\(\small{ \ 8.94^{18} \ }\)の整数部分は何桁か。また最高位からの\(\small{ \ 2 \ }\)桁の数字を求めよ。例えば、\(\small{ \ 12345.6789 \ }\)の最高位からの\(\small{ \ 2 \ }\)桁は\(\small{ \ 12 \ }\)を指す。


\(\small{ \ 8.94^{18} \ }\)の常用対数を考えると
\(\small{ \ \log_{10}8.94^{18}=18\log_{10}8.94 \ }\)
常用対数表より(\(\small{ \ \log_{10}8.94 \ }\)の欄は\(\small{ \ 0.9513 \ }\))
\(\small{ \ 0.95125 \leqq \log_{10}8.94 \lt 0.95135 \ }\)
\(\small{ \ 0.95125\times18 \leqq \log_{10}8.94^{18} \lt 0.95135\times18 \ }\)
\(\small{ \ 17.1225 \leqq \log_{10}8.94^{18} \lt 17.1243 \ }\)
\(\small{ \ 10^{17.1225}\leqq 8.94^{18} \lt 10^{17.1243} \ }\)
よって\(\small{ \ 8.94^{18} \ }\)の整数部分は\(\small{ \ 18 \ }\)桁である
また
\(\small{ \ 10^{17.1225}\leqq 8.94^{18} \lt 10^{17.1243} \ }\)
\(\small{ \ 10^{0.1225}\times10^{17}\leqq 8.94^{18} \lt 10^{0.1243}\times10^{17} \ }\)
常用対数表より(\(\small{ \ \log_{10}1.32 \ }\)の欄は\(\small{ \ 0.1206 \ }\)、\(\small{ \ \log_{10}1.34 \ }\)の欄は\(\small{ \ 0.1271 \ }\))
\(\small{ \ \log_{10}1.32\lt 0.1225\lt0.1243 \lt \log_{10}1.34 \ }\)
\(\small{ \ 8.94^{18} \ }\)の最高位から\(\small{ \ 2 \ }\)桁の数は\(\small{ \ 13 \ }\)である

\(\small{ \ \log_{10}8.94=\log_{10}2+\log_{10}4.47 \ }\)にして
\(\small{ \ 0.30095\leqq \log_{10}2 \lt 0.30105 \ }\)と
\(\small{ \ 0.65025\leqq \log_{10}4.47 \lt 0.65035 \ }\)にわけて
\(\small{ \ 0.95120\leqq \log_{10}8.94 \lt 0.95140 \ }\)として解くことになるからね。
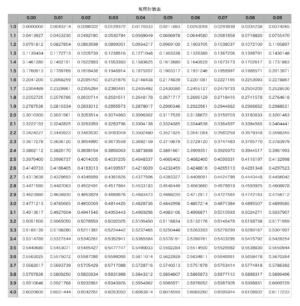
おまけ:常用対数表の作り方
パソコンがあれば簡単に常用対数表を作ることができる。って言っても表計算ソフト(ExcelやNumbersなど)が必要だけどね。
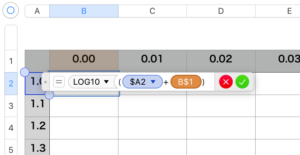
まずは一番左の列に\(\small{ \ 1.0 \ }\)から\(\small{ \ 0.1 \ }\)ずつ増やした値を記入して、一番上の列に\(\small{ \ 0.00 \ }\)から\(\small{ \ 0.09 \ }\)まで\(\small{ \ 0.01 \ }\)ずつ増やした値を記入する。

表計算ソフトには常用対数を求める関数(\(\small{ \ \mathrm{LOG}10 \ }\))が備えてあるから、真数を左の\(\small{ \ \mathrm{A} \ }\)列の値と一番上の行の値を足す式にすればいい。
残りのセルもすべて条件を変えずに、そのセルの一番左の\(\small{ \ \mathrm{A} \ }\)列の値と一番上の\(\small{ \ 1 \ }\)行目の値を足したものを真数として\(\small{ \ \mathrm{LOG}10 \ }\)関数に代入したいから\(\small{ \ \mathrm{$} \ }\)を利用しよう。
\(\small{ \ \mathrm{B}2 \ }\)セルには「\(\small{=\mathrm{LOG}10 \ }\)(\(\small{ \ \mathrm{$A}1+\mathrm{B$}2 \ }\))」って入力しよう。
\(\small{ \ \mathrm{B}2 \ }\)セルをコピーして残りのセルにまとめて貼り付けたら完成。必要に合わせてセルの桁数を変更しよう。

おまけ:常用対数の値と関数電卓
常用対数表がなくても、みんなが持ってるスマートフォンについてる電卓でも常用対数の近似値は簡単に調べることができる。
って言っても関数電卓機能が付いてるやつね。iphoneなら横向きにした電卓ね。調べたい常用対数の真数を入力して\(\small{ \ \log_{10} \ }\)ボタンを押すと表示される。
もちろんスマートフォンじゃなくても関数電卓でも調べることはできるからね。

もちろんこの関数電卓で表示される値も近似値だけどね。

