こんにちは、リンス(@Lins016)です。
今回は三角比について学習していこう。
三角比の定義を確認
今回学習する三角比は数学Iで学習する範囲になるから、角度は\(\small{ \ 0^{\circ}\leqq \theta \leqq 180^{\circ} \ }\)の範囲、つまり三角形で利用できる範囲までってことになるね。
それ以上の角度については数学Ⅱの三角関数で学習するんだけど、数学Ⅰで三角比をきちんと理解しておくことで、三角関数の学習も効率よくできるからしっかりと理解を深めておこう。
三角比とは直角三角形の鋭角に関する辺の比の総称で、数学Iでは下の\(\small{ \ 3 \ }\)つの比の値について学習する。
正弦\(\small{ \ \sin \theta = \displaystyle \frac{a}{c} \ }\)
余弦\(\small{ \ \cos \theta = \displaystyle \frac{b}{c} \ }\)
正接\(\small{ \ \tan \theta = \displaystyle \frac{a}{b} \ }\)

三角形の角は大文字のアルファベットで、辺は小文字のアルファベットで書くから覚えておこう。また角とその対辺のアルファベットの文字は揃えておくことが基本だから注意しよう。
単位円を利用しよう
単位円って半径\(\small{ \ 1 \ }\)の円のことで、\(\small{ \ xy \ }\)平面上に単位円を書くと、単位円の円周上の点の\(\small{ \ x \ }\)座標の値が\(\small{ \ \cos \theta \ }\)、\(\small{ \ y \ }\)座標の値が\(\small{ \ \sin \theta \ }\)になる。
このとき、\(\small{ \ \theta \ }\)は円周上の点と中心を結ぶ線分と\(\small{ \ x \ }\)座標のなす角になるからね。
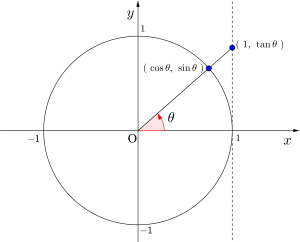
さらに\(\small{ \ \tan \theta \ }\)は円周上の点と中心を結ぶ直線と\(\small{ \ x=1 \ }\)との交点の\(\small{ \ y \ }\)座標になるから覚えておこう。不等式を解くときは特に有効になるからね。
鋭角の三角比は直角三角形を書けば簡単に確認できるけど、鈍角の三角比は単位円を利用して確認しよう。単位円の中に三角形を書いて値を確認することで、失敗しないからね。
また、鈍角の場合、\(\small{ \ \cos \theta \ }\)と\(\small{ \ \tan \theta \ }\)の値が負になるのがわかるよね。
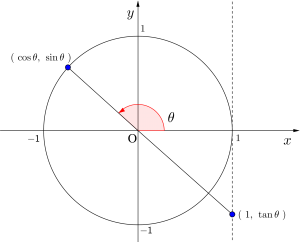
三角比では方程式、不等式を解く問題があるけど、その場合は単位円を利用して問題を解いていくのがベストなやり方だと思うから単位円に慣れておこう。
三角比の値は必ず覚えよう
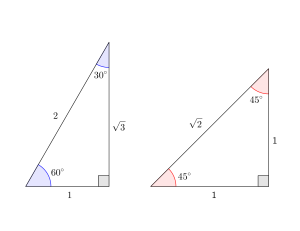
有名な角度の三角比の値はよく使うから覚えておこう。小学生の時に買った三角定規セットの\(\small{ \ 2 \ }\)つの三角形で作られる角が有名角ってことになるからね。
一回一回三角形を書いて調べても答えは求められるけど、そんなに数も多くないから覚えておく方が絶対いいから、覚えてない人は頑張って覚えておこう。
\theta & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ}& 90^{\circ}& 120^{\circ} & 135^{\circ} & 150^{\circ} & 180^{\circ} \\[3pt] \hline
\sin \theta & 0 & \displaystyle \frac{1}{2} & \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{2} & 1 & \displaystyle \frac{\sqrt{3}}{2} & \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{1}{2} & 0 \\[3pt] \hline
\cos \theta & 1 & \displaystyle \frac{\sqrt{3}}{2} & \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{1}{2} & 0 & -\displaystyle \frac{1}{2} & -\displaystyle \frac{\sqrt{2}}{2}& -\displaystyle \frac{\sqrt{3}}{2} & -1 \\[3pt] \hline
\tan \theta & 0 & \displaystyle \frac{1}{\sqrt{3}} & 1 & \sqrt{3} & × & -\sqrt{3} & -1 & -\displaystyle \frac{1}{\sqrt{3}} & 0
\end{array} \ }\)
ちなみに有名角以外の三角比の値は、三角比の表からその表から値を調べるんだけど、その表の値を覚える必要はないからね。その表が必要なときは問題に添付してあるから、覚えなくても問題ないよ。
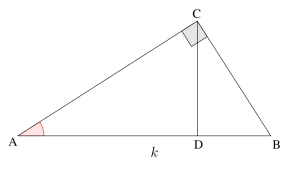
\(\small{ \ \angle \mathrm{C}=90^{\circ} \ }\)である直角三角形\(\small{ \ \mathrm{ABC} \ }\)において、\(\small{ \ \angle \mathrm{A}=\theta \ }\)、\(\small{ \ \mathrm{AB}=k \ }\)とする。頂点\(\small{ \ \mathrm{C} \ }\)から辺\(\small{ \ \mathrm{AB} \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{D} \ }\)とするとき次の値を\(\small{ \ k \ }\)、\(\small{ \ \theta \ }\)を用いて答えよ。
(1)\(\small{ \ \mathrm{BC} \ }\)
(2)\(\small{ \ \mathrm{CD} \ }\)
(3)\(\small{ \ \mathrm{BD} \ }\)
(1)
\(\small{ \begin{eqnarray}\ \mathrm{BC}&=&\mathrm{AB}\sin \theta\\
&=&k\sin \theta \ \end{eqnarray}}\)
(2)
\(\small{\begin{eqnarray} \ \mathrm{CD}&=&\mathrm{AC}\sin \theta\\
&=&\mathrm{AB}\cos \theta \cdot \sin \theta\\
&=&k\sin \theta \cos \theta \ \end{eqnarray}}\)
(3)
\(\small{\begin{eqnarray} \ \mathrm{BD}&=&\mathrm{BC} \sin \theta\\
&=&k \sin^2 \theta \ \end{eqnarray}}\)


Point 三角比
①三角比の有名な値は覚えておく
②単位円の利用に慣れておく

