こんにちは、リンス(@Lins016)です。
今回は三次関数に引ける接線の本数の求め方について学習していこう。
接線の本数の求め方
接線の問題で一番重要なのが接点の座標だよね。これさえわかれば接線の方程式求めることができるからね。
\(\small{ \ y=f(x) \ }\)上にない点\(\small{ \ (a, \ b) \ }\)から接線を引く場合
❶\(\small{ \ y=f(x) \ }\)上の点を\(\small{ \ (t, \ f(t) \ ) \ }\)とおく
❷接線の方程式は
\(\small{ \ y=f'(t)(x-t)+f(t)\cdots① \ }\)
❸\(\small{ \ (a, \ b) \ }\)を通るので、\(\small{①}\)に代入
\(\small{ \ b=f'(t)(a-t)+f(t)\cdots② \ }\)

❹\(\small{ \ ②}\)は\(\small{ \ t \ }\)の方程式より、\(\small{ \ t \ }\)を求めることで、接点の\(\small{ \ x \ }\)座標が求まる
\(\small{ \ t \ }\)の解の数だけ\(\small{ \ (a, \ b) \ }\)から接線を引くことができる
つまり接線の本数を求める問題は接点の個数を求める問題として答えを導いていくんだ。
接線の本数=接点の個数
接線の本数=接点の個数として問題を解いていくわけだけど、これが成り立つのは三次関数までなんだ。
四次以上の関数になると成り立たないから注意しよう。
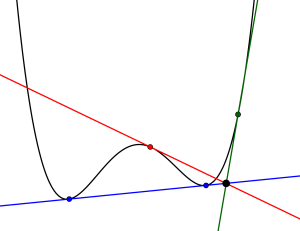
四次以上の関数は、極値を三つ以上持つから、接線が図のように重なる場合がある。
この場合接点の数と接線の本数が一致しないよね。
だから接点の個数=接線の本数が成り立つのは三次以下の関数になるんだけど、基本的に接線の本数を求める問題で四次以上の関数は出てこない。
つまり接線の本数を求めるのは、接点の個数を求めるって覚えておけばいいからね。
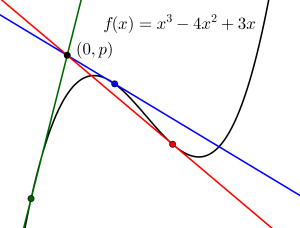
曲線\(\small{ \ f(x)=x^3-4x^2+3x \ }\)に対して、点\(\small{ \ (0, \ p) \ }\)から異なる\(\small{ \ 3 \ }\)本の接線がひけるとき、\(\small{ \ p \ }\)の範囲を求めよ。
\(\small{ \ f(x)=x^3-4x^2+3x \ }\)より
\(\small{ \ f'(x)=3x^2-8x+3 \ }\)
接点の座標を\(\small{ \ (t, \ f(t) \ ) \ }\)とすると
接線の方程式は
\(\small{ \ y=(3t^2-8t+3)(x-t)+t^3-4t^2+3t \ }\)
この直線が点\(\small{ \ (0, \ p) \ }\)を通るので
\(\small{ \ p=(3t^2-8t+3)(-t)+t^3-4t^2+3t \ }\)
これを整理すると
\(\small{ \ p=-2t^3+4t^2 \ }\)
この方程式が\(\small{ \ 3 \ }\)つの異なる解を持てばよいので
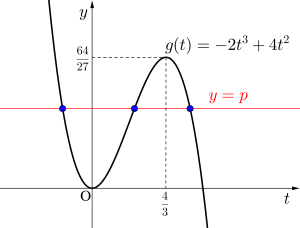
\(\small{ \ g(t)=-2t^3+4t^2 \ }\)とすると
\(\small{ \ y=g(t) \ }\)と\(\small{ \ y=p \ }\)が異なる\(\small{ \ 3 \ }\)つの交点を持てばよい
\(\small{ \ g'(t)=-6t^2+8t=-6t\left(t-\displaystyle \frac{4}{3}\right) \ }\)
増減表を書くと
\(\small{ \ \begin{array}{c|ccccc}
t & \cdots & 0 & \cdots & \displaystyle \frac{4}{3} & \cdots \\
\hline
g’(x) & - & 0 & + & 0 & - \\
\hline
g(x) & \searrow & 0 & \nearrow & \displaystyle \frac{64}{27} & \searrow
\end{array} \ }\)
グラフより求める\(\small{ \ p \ }\)の範囲は
\(\small{ \ 0 \lt p \lt \displaystyle \frac{64}{27} \ }\)

三次方程式の解の個数の求め方(基本)
三次方程式の解の個数の求めた(定数分離)
三次方程式の解の個数の求め方(定数を含む極値の利用)
Point
①接線の本数=接点の個数
②接点の座標を求める方程式をたてる
点\(\small{ \ (a, \ b) \ }\)から曲線\(\small{ \ f(x)=x^3+3x^2-4 \ }\)に異なる\(\small{ \ 3 \ }\)本の接線が引けるとき、\(\small{ \ (a, \ b) \ }\)の存在する範囲を図示せよ。
\(\small{ \ f(x)=x^3+3x^2-4 \ }\)より
\(\small{ \ f'(x)=3x^2+6x \ }\)
接点の座標を\(\small{ \ (t, \ f(t) \ ) \ }\)とすると
接線の方程式は
\(\small{ \ y=(3t^2+6t)(x-t)+t^3+3t^2-4 \ }\)
この直線が点\(\small{ \ (a, \ b) \ }\)を通るので
\(\small{ \ b=(3t^2+6t)(a-t)+t^3+3t^2-4 \ }\)
これを整理すると
\(\small{ \ 2t^3-3(a-1)t^2-6at+b+4=0 \ }\)
この方程式が3つの異なる解を持てばよいので
\(\small{ \ g(t)=2t^3-3(a-1)t^2-6at+b+4 \ }\)とすると
\(\small{ \ y=g(t) \ }\)が極値を持ち、極大値と極小値が異符号であればよい
\(\small{\begin{eqnarray} \ g'(t)&=&6t^2-6(a-1)t-6a\\[ 3pt ]
&=&6(t-a)(t+1) \ \end{eqnarray}}\)
よって\(\small{ \ a \neq 1 \ }\)で\(\small{ \ y=g(t) \ }\)は極値を持つ
さらに\(\small{ \ g(a)g(-1) \lt 0 \ }\)であればよい
\(\small{ \ g(a)=b-a^3-3a^2+4 \ }\)
\(\small{ \ g(-1)=b+3a+5 \ }\)
\(\small{ \ (b+3a+5)(b-a^3-3a^2+4) \lt 0 \ }\)
ここで\(\small{ \ h(a)=a^3+3a^2-4 \ }\)とすると
\(\small{\begin{eqnarray} \ h'(a)&=&3a^2+6a\\[ 3pt ]
&=&3a(a+2) \ \end{eqnarray}}\)
\(\small{ \ \begin{array}{c|ccccc}
a & \cdots & -2 & \cdots & 0 & \cdots \\
\hline
h’(a) & + & 0 & – & 0 & + \\
\hline
h(a) & \nearrow & 0 & \searrow & -4 & \nearrow
\end{array} \ }\)
また\(\small{ \ a^3+3a^2-4=-3a-5 \ }\)とすると
\(\small{ \ a^3+3a^2+3a+1=0 \ }\)
\(\small{ \ (a+1)^3=0 \ }\)
\(\small{ \ \therefore a=-1 \ }\)
よって求める存在範囲は図の斜線部分
ただし、境界線は含まない


