こんにちは、リンス(@Lins016)です。
今回は互いに素な自然数とオイラー関数について学習していこう。
オイラー関数
\(\small{ \ 1 \ }\)から\(\small{ \ n \ }\)までの自然数の中で\(\small{ \ n \ }\)と互いに素な自然数を求めるときに、簡単に求めることが出来るのがオイラー関数なんだ。本当はオイラーの\(\small{ \ \phi \ }\)(ファイ)関数って言うんだけど、高校数学では簡略化してオイラー関数って呼ぶことが多いかな。
でもオイラー関数は教科書に載ってない場合が多いから、ここできちんと理解しておこう。入試で出題されることもあるからね。
\(\small{ \ n \ }\)以下の自然数で\(\small{ \ n \ }\)と互いに素である自然数の個数\(\small{ \ \phi(n) \ }\)は
\(\small{ \ \phi(n)=n\displaystyle \prod_{ i = 1 }^k\left(1-\displaystyle\frac{1}{p_i}\right) \ }\)
ただし\(\small{ \ p_i \ }\)は\(\small{ \ n \ }\)の素因数
\(\small{ \ n=2^a\cdot3^b\cdot5^c \ }\)のとき
\(\small{ \ \phi(n)=n\left(1-\displaystyle\frac{1}{2}\right)\left(1-\displaystyle\frac{1}{3}\right)\left(1-\displaystyle\frac{1}{5}\right) \ }\)
互いに素な数の求め方
まずはオイラー関数を使わないやり方で\(\small{ \ 108 \ }\)と互いに素である\(\small{ \ 108 \ }\)以下の自然数の個数を考えてみよう。
\(\small{ \ 108 \ }\)を素因数分解すると\(\small{ \ 108=2^2\times3^3 \ }\)だからつまり\(\small{ \ 108 \ }\)と互いに素になる自然数は約数に\(\small{ \ 2 \ }\)と\(\small{ \ 3 \ }\)を持たないってことになるよね。
\(\small{ \ 1 \ }\)~\(\small{ \ 108 \ }\)までの自然数のうち\(\small{ \ 2 \ }\)を約数に持つ(つまり\(\small{ \ 2 \ }\)の倍数である)自然数の個数は\(\small{ \ n(\mathrm{A})=\displaystyle\frac{108}{2}=54 \ }\)個。
同様に\(\small{ \ 1 \ }\)~\(\small{ \ 108 \ }\)までの自然数のうち\(\small{ \ 3 \ }\)を約数に持つ(つまり\(\small{ \ 3 \ }\)の倍数である)自然数の個数は\(\small{ \ n(\mathrm{B})=\displaystyle\frac{108}{3}=36 \ }\)個。
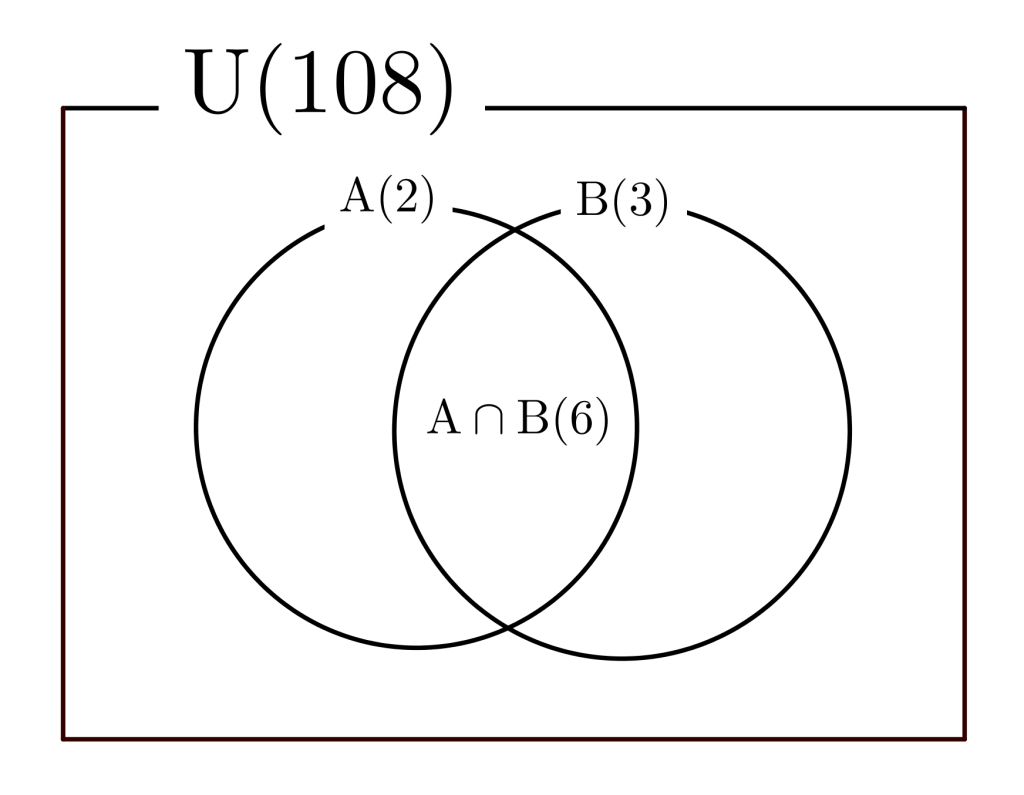
この\(\small{ \ 54 \ }\)個と\(\small{ \ 36 \ }\)個のうち\(\small{ \ 2 \ }\)の倍数かつ\(\small{ \ 3 \ }\)の倍数である共通のものが含まれているよね。それは\(\small{ \ 6 \ }\)を約数にもつ(\(\small{ \ 6 \ }\)の倍数である)自然数になるから\(\small{ \ n(\mathrm{A\cap B})=\displaystyle\frac{108}{6}=18 \ }\)
だから\(\small{ \ 108 \ }\)と互いに素である\(\small{ \ 108 \ }\)以下の自然数の個数は
\(\small{ \ 108-\left(54+36-18\right)=36 \ }\)個になるんだ。
集合の要素の個数については下の記事を復習しておこう。
オイラー関数への変形
\(\small{ \ 108 \ }\)と互いに素である\(\small{ \ 108 \ }\)以下の自然数の個数は\(\small{ \ 36 \ }\)個だったけど、この式をオイラー関数の形に変形してみよう。
\(\small{ \ 108-\left(54+36-18\right)\\[10pt]
=108-\left(\displaystyle\frac{108}{2}+\displaystyle\frac{108}{3}-\displaystyle\frac{108}{6}\right)\\
=108\left\{1-\left(\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{6}\right)\right\}\\
=108\left(1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{6}\right)\\
=108\left(1-\displaystyle\frac{1}{2}\right)\left(1-\displaystyle\frac{1}{3}\right) \ }\)
この式が\(\small{ \ 108 \ }\)のオイラー関数の式になるんだ。
「\(\small{ \ 1-\displaystyle\frac{1}{2} \ }\)」の部分は\(\small{ \ 2 \ }\)を約数に持たないものが半分って考えることができるし、\(\small{ \ 2 \ }\)を約数に持たないものにさらに「\(\small{ \ 1-\displaystyle\frac{1}{3} \ }\)」をかけることによって\(\small{ \ 3 \ }\)を約数に持たないものが\(\small{ \ \displaystyle\frac{2}{3} \ }\)あるって考えることができるよね。
オイラー関数
次にオイラー関数\(\small{ \ \phi(n) \ }\)について考えていこう。
①素数\(\small{ \ p \ }\)に対して\(\small{ \ \phi(p)=p-1 \ }\)
\(\small{ \ p \ }\)が素数なら\(\small{ \ 1 \ }\)から\(\small{ \ p-1 \ }\)のうち\(\small{ \ p \ }\)の素因数である\(\small{ \ p \ }\)を因数に持つものは存在しないから\(\small{ \ \phi(p)=p-1 \ }\)になるよね。
②素数\(\small{ \ p \ }\)、自然数\(\small{ \ n \ }\)に対して\(\small{ \ \phi\left(p^n\right)=p^n-p^{n-1}=p^n\left(1-\displaystyle\frac{1}{p}\right) \ }\)
\(\small{ \ 1 \ }\)から\(\small{ \ p^n \ }\)の中で\(\small{ \ p \ }\)を因数として持つもの(つまり\(\small{ \ p \ }\)の倍数)は\(\small{ \ p^{n-1} \ }\)個あるから互いに素になる数は\(\small{ \ p^n-p^{n-1} \ }\)個ある。
\(\small{ \ 1 \ }\)から\(\small{ \ p^n \ }\)の中で\(\small{ \ p \ }\)を因数として持つもの(つまり\(\small{ \ p \ }\)の倍数)は\(\small{ \ p^{n-1} \ }\)個あるってところがすこしわかりにくいけど、 \(\small{ \ p \ }\)の倍数だけ取り出して書くと
\(\small{ \ p, \ 2p, \ 3p,\cdots, \ p^{n-2}p, \ p^{n-1}p \ }\)ってなるから\(\small{ \ p \ }\)の倍数は\(\small{ \ p^{n-1} \ }\)個あるよね。
③異なる素数\(\small{ \ p, \ q \ }\)に対して\(\small{ \ \phi(pq)=(p-1)(q-1)=pq\left(1-\displaystyle\frac{1}{p}\right)\left(1-\displaystyle\frac{1}{q}\right) \ }\)
この式は合同式を利用した証明とか色々な証明方法があるけど、今回は感覚的にこの式を掴んでみよう。
\(\small{ \ p, \ q \ }\)は素数だから\(\small{ \ pq \ }\)以下の自然数で\(\small{ \ p \ }\)の倍数は\(\small{ \ q \ }\)個、\(\small{ \ q \ }\)の倍数は\(\small{ \ p \ }\)個あるよね。
その内共通なものは\(\small{ \ pq \ }\)の\(\small{ \ 1 \ }\)個しかないから\(\small{ \ p, \ q \ }\)を因数に持つ\(\small{ \ pq \ }\)以下の自然数は\(\small{ \ p+q-1 \ }\)個ある。
だから\(\small{ \ pq \ }\)と互いに素になる数は
\(\small{ \ pq-(p+q-1)=(p-1)(q-1) \ }\)個ってことになるよね。
この①②③を利用することで自然数\(\small{ \ n=2^a3^b5^c \ }\)と互いに素である\(\small{ \ n \ }\)以下の自然数は\(\small{ \ n\left(1-\displaystyle\frac{1}{2}\right)\left(1-\displaystyle\frac{1}{3}\right)\left(1-\displaystyle\frac{1}{5}\right) \ }\)って言えるんだ。
\(\small{ \ 504 \ }\)以下の自然数で\(\small{ \ 504 \ }\)と互いに素な自然数について答えよ。
(1)このような自然数はいくつあるか。
(2)このような自然数の和はいくつになるか。
(1)\(\small{ \ 504=2^3\times3^2\times7 \ }\)より
\(\small{ \ 504\left(1-\displaystyle\frac{1}{2 }\right)\left(1-\displaystyle\frac{1}{3 }\right)\left(1-\displaystyle\frac{1}{7 }\right)\\
=144 \ }\)
(2)自然数\(\small{ \ k \ }\)が\(\small{ \ 504 \ }\)と互いに素なら\(\small{ \ 504-k \ }\)も互いに素である
この\(\small{ \ 2 \ }\)つの数の和は\(\small{ \ 504 \ }\)になる
\(\small{ \ 504 \ }\)と互いに素になる自然数は全部で\(\small{ \ 144 \ }\)個あるから
\(\small{ \ 504\times\displaystyle\frac{144}{2 }=36288 \ }\)

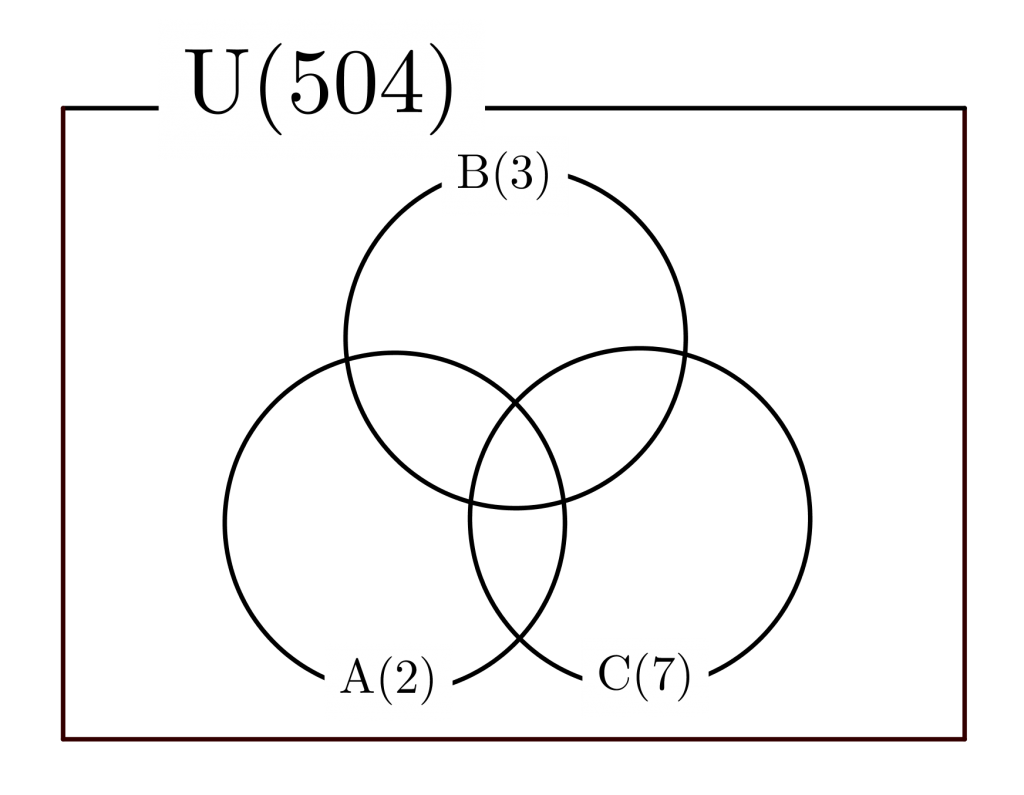
ちなみにこの問題を集合で考えてとくと
\ \ -n(\mathrm{A}\cap\mathrm{B})-n(\mathrm{A}\cap\mathrm{C})-n(\mathrm{B}\cap\mathrm{C})\\
\ \ \ \ +n(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}) }\)
を利用することになるよね。
つまり\(\small{ \ n(\mathrm{U})-n(\mathrm{A}\cup\mathrm{B}\cup\mathrm{C}) \ }\)ってことだからね。
Point 互いに素な自然数とオイラー関数
①互いに素は共通の約数を持たないこと
②オイラー関数の式の原理を理解する
自然数\(\small{ \ n \ }\)に対して、\(\small{ \ n \ }\)以下の自然数で\(\small{ \ n \ }\)との最大公約数が\(\small{ \ 1 \ }\)であるような自然数の個数を\(\small{ \ f(n) \ }\)とする。例えば、\(\small{ \ n=12 \ }\)に対しては、このような自然数は、\(\small{ \ 1, \ 5, \ 7, \ 11 \ }\)の\(\small{ \ 4 \ }\)個なので、\(\small{ \ f(12)=4 \ }\)である。また、\(\small{ \ f(1)=1 \ }\)、素数\(\small{ \ p \ }\)に対しては\(\small{ \ f(p)=p-1 \ }\)である。
(1)\(\small{ \ f(77) \ }\)の値を求めよ。
(2)\(\small{ \ f(pq)=24 \ }\)となる\(\small{ \ 2 \ }\)つの素数\(\small{ \ p, \ q \ }\)(ただし、\(\small{ \ p\lt q \ }\)とする)の組を求めよ。
(3)\(\small{ \ k, \ n \ }\)を自然数とするとき、\(\small{ \ f(2^k3^n) \ }\)の値を\(\small{ \ k \ }\)と\(\small{ \ n \ }\)の式で表せ。
(1)\(\small{ \ 77=7\times11 \ }\)より
\(\small{\begin{eqnarray} \ f(77)&=&77-\left(\displaystyle\frac{77}{7}+\displaystyle\frac{77}{11}-\displaystyle\frac{77}{7\times11 }\right)\\
&=&60 \ \end{eqnarray}}\)
(2)\(\small{ \ p, \ q \ }\)は素数だから
\(\small{\begin{eqnarray} \ f(pq)&=&pq-\left(\displaystyle\frac{pq}{p}+\displaystyle\frac{pq}{q}-\displaystyle\frac{pq}{p\times q }\right)\\
&=&pq-p-q+1\\
&=&(p-1)(q-1) \ \end{eqnarray}}\)
\(\small{ \ f(pq)=24 \ }\)より
\(\small{ \ (p-1)(q-1)=24 \ }\)
\(\small{ \ p, \ q \ }\)は素数かつ\(\small{ \ p\lt q \ }\)より
\(\small{\begin{array}{c|cccc} \ p-1&1&2&3&4\\
\hline
q-1&24&12&8&6 \ \end{array}}\)
\(\small{\begin{array}{c|cccc} \ p&2&3&4&5\\
\hline
q&25&13&9&7 \ \end{array}}\)
\(\small{ \ p, \ q \ }\)は素数より
\(\small{ \ (p, \ q)=(3, \ 13), \ (5, \ 7) \ }\)
(3)
&=&2^k3^n-2^k3^{n-1}-2^{k-1}3^n+2^{k-1}3^{n-1}\\
&=&2^{k-1}3^{n-1}\left(6-2-3+1\right)\\
&=&2^k3^{n-1} \ \end{eqnarray}}\)

ここで気になるのがオイラー関数を入試に使っていいのかってこと。この辺についてはまた別な記事で紹介しようと思う。
学校で教わらないけど入試に使いたい式って結構あるもんね。
ただ使うか使わないかに関わらず便利な式であることは間違いないから、使わないにしても検算用に覚えておくことは重要だよ。

