対数関数の微分とグラフと絶対値

こんにちは、リンス(@Lins016)です。
今回は対数関数の微分とグラフと絶対値について学習していこう。

対数関数の微分と絶対値

今回は知識としての知ってほしいことを書いて行くから、例題とかはないけど、すごく重要なことだからきちんと確認しておこう。

\(\small{ \ y=\log x \ }\)と\(\small{ \ y=\log \vert x\vert \ }\)のグラフを考えながら、対数関数の微分について考えよう。
まずはこの記事を勉強する前に微分の基本的なことを確認しておこう。

対数関数のグラフと真数条件

対数\(\small{ \ \log_a b \ }\)の\(\small{ \ a \ }\)を底、\(\small{ \ b \ }\)を真数っていうんだったよね。
真数は正の数じゃないといけなかったよね。このことを真数条件って言ったよね。

\(\small{ \ y=\log x \ }\)のグラフは真数条件より定義域は\(\small{ \ x\gt 0 \ }\)だからグラフはこうなるよね。

それに対して\(\small{ \ y=\log \vert x\vert \ }\)のグラフは真数条件より\(\small{ \ \vert x\vert\gt 0 \ }\)だから、定義域は\(\small{ \ x\lt0, \ x\gt 0 \ }\)になってグラフはこうなるよね。

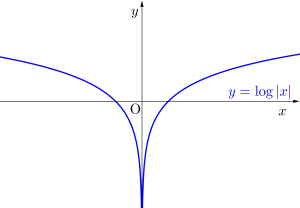
真数に絶対値がある場合は定義域に注意しよう。

対数関数の微分

微分するっていうのは導関数を求めるってことだけど、導関数って接線の傾きを関数にしたものだよね。

\(\small{ \ \log x \ }\)を微分すると\(\small{ \ \displaystyle\frac{1}{x} \ }\)になるんだよね。

それじゃ\(\small{ \ \log \vert x \vert \ }\)を微分すると\(\small{ \ \displaystyle\frac{1}{\vert x\vert } \ }\)になるのかな？
その答えはNOなんだ。

\(\small{ \ y=\log \vert x \vert \ }\)を微分して\(\small{ \ y'=\displaystyle\frac{1}{\vert x\vert } \ }\)になるなら、\(\small{ \ y'\gt0 \ }\)だから\(\small{ \ y=\log \vert x \vert \ }\)は単調増加のグラフじゃないといけないよね。
でも実際のグラフはさっきも確認したけど、\(\small{ \ x\lt0 \ }\)で減少関数、\(\small{ \ x\gt0 \ }\)で増加関数だよね。

グラフで接線の傾きを考えてみよう。
\(\small{ \ x=a \ }\)のとき接線の傾きは\(\small{ \ \displaystyle\frac{1}{a} \ }\)
この\(\small{ \ y=\log \vert x \vert \ }\)は\(\small{ \ y \ }\)軸に関して対称だから
\(\small{ \ x=-a \ }\)のとき接線の傾きは\(\small{ \ -\displaystyle\frac{1}{a} \ }\)になるよね。

だから\(\small{ \ y=\log \vert x \vert \ }\)を微分しても\(\small{ \ y'=\displaystyle\frac{1}{x } \ }\)になって絶対値が必要なくなるんだ。
数学Ⅲは記述式の試験になるから、減点されないよう絶対値の処理をきちんとしよう。

Point 対数関数の微分とグラフと絶対値

①\(\small{ \ y=\log \vert x \vert \ }\)の定義域とグラフを確認
②\(\small{ \ y=\log \vert x \vert \ }\)のとき\(\small{ \ y'=\displaystyle\frac{1}{\vert x \vert} \ }\)は間違い\(\small{ \ y'=\displaystyle\frac{1}{x} \ }\)