こんにちは、リンス(@Lins016)です。今回は対数関数と真数条件について学習していこう。
真数条件とは
対数\(\small{ \ \log_ab \ }\)の\(\small{ \ a \ }\)を底、\(\small{ \ b \ }\)を真数っていうんだけど、底も真数も正の値じゃないといけないんだ。特に真数が正の値になることを真数条件って言うんだ。
\(\small{ \ \log_ab=N \ }\)は\(\small{ \ b=a^N \ }\)って変形できるから、\(\small{ \ a\gt0 \ }\)なら\(\small{ \ b\gt0 \ }\)になるからね。
このことは指数関数のグラフを考えてもわかるよね。
今回はこの真数条件をより深く考えてみよう。
真数条件
\(\small{ \ \log_af(x) \ }\)のとき\(\small{ \ f(x)\gt0 \ }\)
問題文と真数条件
真数条件は真数が正になることだけど、次の\(\small{ \ 2 \ }\)つの式の真数条件を考えてみよう。
①\(\small{ \ \log_2(x-2)+\log_2(x-4) \ }\)
②\(\small{ \ \log_2(x-2)(x-4) \ }\)
底が同じ対数の和は、真数の積の形に変形できたよね。
\(\small{ \ \log_aM+\log_aN=\log_aMN \ }\)
だから①と②は同じ式になるから、真数条件も同じかっていうとそうじゃないんだ。
①の真数条件は『\(\small{ \ x-2\gt0 \ }\)かつ\(\small{ \ x-4\gt0 \ }\)』でこれを満たす\(\small{ \ x\gt4 \ }\)になる。
これに対して②の真数条件は『\(\small{ \ (x-2)(x-4)\gt0 \ }\)』でこれを満たす\(\small{ \ x\lt2 \ }\)または\(\small{ \ x\gt4 \ }\)になるんだ。
たしかに①の式に\(\small{ \ x=1 \ }\)を代入すると真数は負になるからダメだけど、②の式に\(\small{ \ x=1 \ }\)を代入すると真数は正になるからね。
だから真数条件は『問題文で与えられた式を変形する前』に考えないといけないって事になる。
問題文に①の\(\small{ \ \log_2(x-2)+\log_2(x-4) \ }\)って書いてあったら真数条件は\(\small{ \ x\gt 4 \ }\)になるし、②の\(\small{ \ \log_2(x-2)(x-4) \ }\)って書いてあったら、\(\small{ \ x\lt2, \ x\gt4 \ }\)になるからね。
常に真数条件は問題文から考えるようにしよう。
真数条件とグラフ
次に\(\small{ \ y=2\log_2x \ }\)と\(\small{ \ y=\log_2x^2 \ }\)について考えてみよう。
\(\small{ \ y=2\log_2x \ }\)の真数条件は\(\small{ \ x\gt0 \ }\)、\(\small{ \ y=\log_2x^2 \ }\)の真数条件は\(\small{ \ x^2\gt0 \ }\)から\(\small{ \ x\lt0, \ x\gt 0 \ }\)になるよね。
だからグラフは次のようになるんだ。

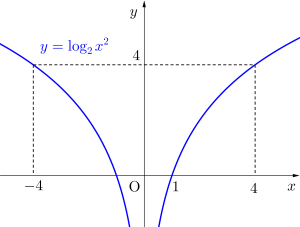
もちろんこの\(\small{ \ 2 \ }\)つのグラフは\(\small{ \ x\gt0 \ }\)の部分は同じグラフだからね。
ここで\(\small{ \ f(x)=\log_2x^2 \ }\)とすると\(\small{ \ f(-x)=\log_2(-x)^2=\log_2x^2=f(x) \ }\)になるから\(\small{ \ y \ }\)軸対称なグラフ、つまり偶関数になる。
だから\(\small{ \ y=\log_2x^2 \ }\)のグラフは\(\small{ \ y=2\log_2x \ }\)のグラフとそれを\(\small{ \ y \ }\)軸に対称移動させたグラフになるんだ。
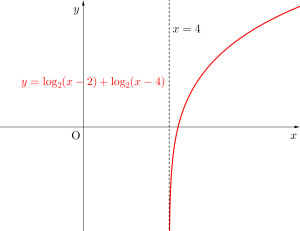
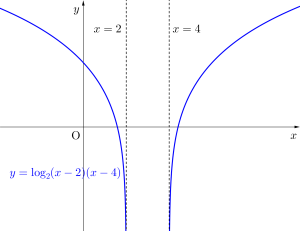
ちなみに\(\small{ \ y=\log_2(x-2)+\log_2(x-4) \ }\)のグラフと\(\small{ \ y=\log_2(x-2)(x-4) \ }\)のグラフは真数条件に注意して書くと下のグラフになって、\(\small{ \ x\gt4 \ }\)の部分は同じグラフになるからね

Point 対数関数と真数条件
①\(\small{ \ \log_af(x) \ }\)のとき\(\small{ \ f(x)\gt0 \ }\)
②真数条件は問題文で考える

