こんにちは、リンス(@Lins016)です。
今回は点対称・線対称・面対称について学習していこう。
対称な点の求め方
平面ベクトルだと対称は点対称と線対称だけだったけど、空間中の対称はこれに加えて面対称があるよね。今回は空間座標中の対称点の求め方を覚えてしまおう。
・点対称
対称点の中点を利用する
・軸対称
軸以外の座標の符号が反転
・線対称
元の点と対称点を結ぶ線分が直線と垂直に交わる
元の点と対称点の中点が直線上にある
・面対称
法線ベクトルを利用する
点対称
点\(\small{ \ \mathrm{A}(a, \ b, \ c) \ }\)に関して点\(\small{ \ \mathrm{P}(p, \ q, \ r) \ }\)と対称な点\(\small{ \ \mathrm{Q}(x_1, \ y_1, \ z_1) \ }\)の座標を求める場合、点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の中点が点\(\small{ \ \mathrm{A} \ }\)になるよね。
つまり
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle\frac{x_1+p}{2}=a \\
\displaystyle\frac{y_1+q}{2}=b\\
\displaystyle\frac{z_1+r}{2}=c
\end{array}
\right.
\end{eqnarray} \ }\)が成り立つってこと。

だから点対称の場合は中点を利用して求めよう。それが簡単だからね。
あと、点対称を求める場合はどの点に関して対称なのか問題文をよく読もう。
「点\(\small{ \ \mathrm{A} \ }\)に関して対称」って言われたら点\(\small{ \ \mathrm{A} \ }\)が中点になるってことだからね。よく問題文を読み間違えて点\(\small{ \ \mathrm{A} \ }\)の対称点を求めようってする人を見かけるから注意しよう。
点\(\small{ \ \mathrm{A}(2, \ 0, \ 3) \ }\)に関して、点\(\small{ \ \mathrm{P}(4, \ -2, \ 5) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標を求めよ。
点\(\small{ \ \mathrm{A} \ }\)に関して、点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)は対称だから点\(\small{ \ \mathrm{A} \ }\)は点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の中点である
\(\small{ \ \mathrm{Q} \ }\)の座標を\(\small{ \ (x, \ y, \ z) \ }\)とすると
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle\frac{x+4}{2}=2 \\
\displaystyle\frac{y-2}{2}=0\\
\displaystyle\frac{z+5}{2}=3
\end{array}
\right.
\end{eqnarray} \ }\)
これを解いて
\(\small{ \ (x, \ y, \ z)=(0, \ 2, \ 1) \ }\)
軸対称
次は線対称について考えていくんだけど、まずは直線の中でも特別な直線になる軸に関して対称な点について考えてみよう。
軸っていうのは\(\small{ \ x \ }\)軸や\(\small{ \ y \ }\)軸、\(\small{ \ z \ }\)軸のことね。この軸に関して対称な点は簡単に求めることができるから、他の直線に関して対称な場合と求め方は違うんだ。
\(\small{ \ z \ }\)軸に関して点\(\small{ \ \mathrm{P}(p, \ q, \ r) \ }\)と対称な点\(\small{ \ \mathrm{Q}(x_1, \ y_1, \ z_1) \ }\)について考えてみよう。
\(\small{ \ z \ }\)軸に関して対称だから点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)は\(\small{ \ z=r \ }\)平面上にある。
つまり\(\small{ \ z_1=r \ }\)ってこと。
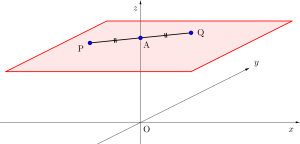
さらに\(\small{ \ z \ }\)軸を上から見たら図のように点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)は\(\small{ \ z=r \ }\)平面上で、原点(\(\small{ \ z \ }\)軸)に関して対称な図形になる。
だから\(\small{ \ x_1=-p \ }\)、\(\small{ \ y_1=-q \ }\)になるんだ。
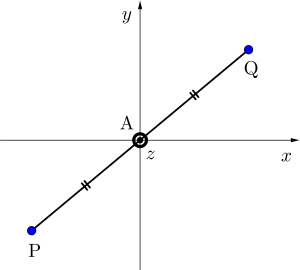
つまり\(\small{ \ z \ }\)軸に関して対称な点を求める場合、\(\small{ \ z \ }\)座標は同じで、\(\small{ \ x \ }\)座標・\(\small{ \ y \ }\)座標ともに符合が変わることになる。
同じように\(\small{ \ x \ }\)軸に関して対称な点なら\(\small{ \ x \ }\)座標が同じで、残りの座標の符号が変わるし、\(\small{ \ y \ }\)軸に関して対称な点なら\(\small{ \ y \ }\)座標が同じで、残りの座標の符号が変わるんだ。
\(\small{ \ z \ }\)軸に関して、点\(\small{ \ \mathrm{P}(4, \ -2, \ 5) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標を求めよ。
また、\(\small{ \ y \ }\)軸に関して、点\(\small{ \ \mathrm{P} \ }\)と対称な点\(\small{ \ \mathrm{R} \ }\)の座標も求めよ。
\(\small{ \ z \ }\)軸に関して、点\(\small{ \ \mathrm{P}(4, \ -2, \ 5) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標は
\(\small{ \ z \ }\)座標以外の符号が変わるので
\(\small{ \ (x, \ y, \ z)=(-4, \ 2, \ 5) \ }\)
同様に\(\small{ \ y \ }\)軸に関して、点\(\small{ \ \mathrm{P}(4, \ -2, \ 5) \ }\)と対称な点\(\small{ \ \mathrm{R} \ }\)の座標は
\(\small{ \ y \ }\)座標以外の符号が変わるので
\(\small{ \ (x, \ y, \ z)=(-4, \ -2, \ -5) \ }\)
線対称
次は空間中の直線に関して対称な点について考えてみよう。
空間中の直線\(\small{ \ l \ }\)に関して点\(\small{ \ \mathrm{P}(p, \ q, \ r) \ }\)と対称な点\(\small{ \ \mathrm{Q}(x_1, \ y_1, \ z_1) \ }\)の関係式を導いてみよう。
平面のときと同じで関係式は次の\(\small{ \ 2 \ }\)つの関係から立てよう。
それは
①線分\(\small{ \ \mathrm{PQ} \ }\)と直線\(\small{ \ l \ }\)は垂直である
② \(\small{ \ \mathrm{PQ} \ }\)の中点は直線\(\small{ \ l \ }\)上にある
ってこと。
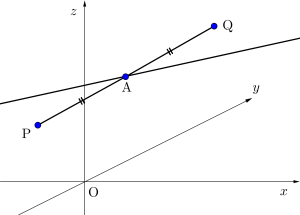
ここで注意しておきたいのは、\(\small{ \ \mathrm{PQ} \ }\)と垂直になるのは直線\(\small{ \ l \ }\)の方向ベクトルだからね。
この\(\small{ \ 2 \ }\)つを頭に入れて例題を解いてみよう。
空間中に直線\(\small{ \ l \ }\)\(\small{ \ \displaystyle\frac{x-1}{-1}=\displaystyle\frac{y-4}{-2}=z-3 \ }\)がある。
直線\(\small{ \ l \ }\)に関して、点\(\small{ \ \mathrm{P}(-1, \ 2, \ 3) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標を求めよ。
点\(\small{ \ \mathrm{Q} \ }\)の座標を\(\small{ \ (a, \ b, \ c) \ }\)とする
\(\small{ \ \mathrm{PQ} \ }\)と直線\(\small{ \ l \ }\)は垂直より
\(\small{ \ \therefore -a-2b+c=0\cdots① \ }\)
直線\(\small{ \ l \ }\)を媒介変数\(\small{ \ t \ }\)を利用して表すと
\(\small{ \ (x, \ y, \ z)=(-t+1, \ -2t+4, \ t+3) \ }\)
点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の中点は\(\small{ \ l \ }\)上にあるので
これを整理して
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
a=-2t+3 \\
b=-4t+6\\
c=2t+3
\end{array}
\right.
\end{eqnarray}\cdots② \ }\)
\(\small{ \ ①, \ ② \ }\)より\(\small{ \ t=1, \ (a, \ b, \ c)=(1, \ 2, \ 5) \ }\)
点\(\small{ \ \mathrm{P} \ }\)から直線\(\small{ \ l \ }\)に下ろした垂線の足を\(\small{ \ \mathrm{H} \ }\)とする
\(\small{ \ \mathrm{H} \ }\)の座標は直線\(\small{ \ l \ }\)上にあるので\(\small{ \ (-t+1, \ -2t+4, \ t+3) \ }\)とおける
\(\small{ \ \mathrm{PH} \ }\)は直線\(\small{ \ l \ }\)に垂直だから
これを解いて\(\small{ \ t=1 \ }\)
よって\(\small{ \ \mathrm{H}(0, \ 2, \ 4) \ }\)
点\(\small{ \ \mathrm{H} \ }\)は点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の中点だから
\(\small{ \ \mathrm{Q} \ }\)の座標を\(\small{ \ (a, \ b, \ c) \ }\)とすると
\(\small{ \ \left(\displaystyle\frac{a-1}{2}, \ \displaystyle\frac{b+2}{2}, \ \displaystyle\frac{c+3}{2}\right)=(0, \ 2, \ 4) \ }\)
これより
\(\small{ \ (a, \ b, \ c)=(1, \ 2, \ 5) \ }\)

面対称(基礎)
次はある平面に関して対称な点を学習していくけど、まずは軸に垂直な平面の場合について考えていこう。
軸に垂直な平面っていうのは、\(\small{ \ ax+by+cz+d=0 \ }\)の形のうち\(\small{ \ x, \ y, \ z \ }\)の係数が\(\small{ \ 2 \ }\)つ\(\small{ \ 0 \ }\)の平面のことね。
例えば\(\small{ \ z \ }\)軸に垂直な平面だと\(\small{ \ z=\alpha \ }\)の形をした平面のこと。
\(\small{ \ z \ }\)軸に垂直な平面に関して対称な点は、\(\small{ \ x \ }\)座標、\(\small{ \ y \ }\)座標ともに変化なしで、\(\small{ \ z \ }\)座標だけ変化するってことね。
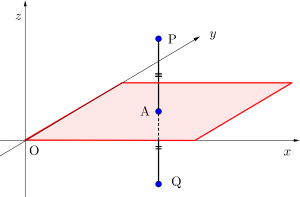
\(\small{ \ xy \ }\)平面に関して、点\(\small{ \ \mathrm{P}(4, \ -2, \ 5) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標を求めよ。
また、平面\(\small{ \ y=4 \ }\)に関して、点\(\small{ \ \mathrm{P} \ }\)と対称な点\(\small{ \ \mathrm{R} \ }\)の座標も求めよ。
\(\small{ \ xy \ }\)平面に関して、点\(\small{ \ \mathrm{P}(4, \ -2, \ 5) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標は
\(\small{ \ z \ }\)座標の符号が変わるので
\(\small{ \ \mathrm{Q}(4, \ -2, \ -5) \ }\)
平面\(\small{ \ y=4 \ }\)に関して、点\(\small{ \ \mathrm{P} \ }\)と対称な点\(\small{ \ \mathrm{R} \ }\)の座標は\(\small{ \ (4, \ a, \ 5) \ }\)とおける
点\(\small{ \ \mathrm{P} \ }\)の\(\small{ \ y \ }\)座標と点\(\small{ \ \mathrm{R} \ }\)の\(\small{ \ y \ }\)座標の中点が平面\(\small{ \ y=4 \ }\)上にあればいいので
\(\small{ \ \displaystyle\frac{a-2}{2}=4 \ }\)
\(\small{ \ a=10 \ }\)
よって求める\(\small{ \ \mathrm{R} \ }\)の座標は\(\small{ \ (4, \ 10, \ 5) \ }\)
面対称
最後に\(\small{ \ ax+by+cz+d=0 \ }\)に関して対称な点について考えてみよう。
平面に関して点\(\small{ \ \mathrm{P} \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)を結ぶ線分は平面に垂直になるんだ。
つまり点\(\small{ \ \mathrm{P} \ }\)から平面に下ろした垂線の足が点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の中点になる。
さらに\(\small{ \ \mathrm{PQ} \ }\)が平面の法線ベクトルに平行ってことにもなるよね。
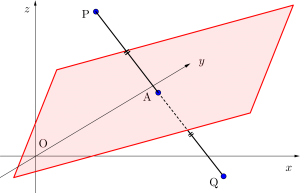
このことを利用して例題を解いてみよう。
\(\small{ \ x+2y-3z-2=0 \ }\)に関して点\(\small{ \ \mathrm{P}(3, \ 6, \ -5) \ }\)と対称な点\(\small{ \ \mathrm{Q} \ }\)の座標を求めよ。
点\(\small{ \ \mathrm{P} \ }\)を通り平面\(\small{ \ x+2y-3z-2=0 \ }\)に垂直な直線上の点は媒介変数\(\small{ \ t \ }\)を用いて
\(\small{\begin{eqnarray} \ (x, \ y, \ z)&=&(3, \ 6, \ -5)+t(1, \ 2, \ -3)\\
&=&(t+3, \ 2t+6, \ -3t-5) \ \end{eqnarray}}\)
直線と平面の交点の座標は
\(\small{ \ t+3+2(2t+6)-3(-3t-5)-2=0 \ }\)
これを解いて
\(\small{ \ t=-2 \ }\)
よって対称な点\(\small{ \ \mathrm{Q} \ }\)の座標は\(\small{ \ t=-4 \ }\)のとき
よって求める座標は\(\small{ \ (-1, \ -2, \ 7) \ }\)
\(\small{ \ \mathrm{Q} \ }\)の座標を\(\small{ \ (a, \ b, \ c) \ }\)とする
\(\small{ \ \mathrm{PQ} \ }\)は平面と垂直に交わるので法線ベクトルに平行
\(\small{ \ (a-3, \ b-6, \ c+5)=k(1, \ 2, \ -3) \ }\)
\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
a=k+3 \\
b=2k+6\\
c=-3k-5
\end{array}
\right.
\end{eqnarray}\cdots① \ }\)
点\(\small{ \ \mathrm{P} \ }\)と点\(\small{ \ \mathrm{Q} \ }\)の中点は平面上にあるので、
\(\small{ \ a+2b-3c+26=0\cdots② \ }\)
\(\small{ \ ①, \ ② \ }\)より
\(\small{ \ k=-4 \ }\)
\(\small{ \ (a, \ b, \ c)=(-1, \ -2, \ 7) \ }\)

Point 点対称・線対称・面対称
①点対称は中点を利用する
②線対称は「中点が直線上」と「線分が直線と垂直に交わる」を利用する
③面対称は「平面の法線ベクトル」を利用する

