空間ベクトル

空間ベクトルと三角形の面積

重要度　難易度

こんにちは、リンス(@Lins016)です。
今回は空間ベクトルと三角形の面積について学習していこう。

スポンサーリンク

空間中の三角形の面積の求め方

空間ベクトルで三角形の面積を求める問題は\(\small{ \ 2 \ }\)つのパターンがある。
それは「成分表示でないベクトルの問題」と「成分表示のベクトルの問題」。
この\(\small{ \ 2 \ }\)つのパターンを確実にできるようにしていこう。

空間ベクトルと三角形の面積

・成分表示でない問題
\(\small{ \ \triangle\mathrm{ABC} \ }\)の面積を\(\small{ \ \mathrm{S} \ }\)とすると
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{AB}}\vert^2\vert\overrightarrow{\mathrm{AC}}\vert^2-\left(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\right)^2} \ }\)

・成分表示の問題
\(\small{ \ \overrightarrow{a}=(a_1, \ a_2, \ a_3) \ }\)
\(\small{ \ \overrightarrow{b}=(b_1, \ b_2, \ b_3) \ }\)
\(\small{ \ \overrightarrow{a} \ }\)、\(\small{ \ \overrightarrow{b} \ }\)の作る三角形の面積\(\small{ \ \mathrm{S} \ }\)は

\(\small{\begin{eqnarray}\mathrm{S}&=&\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{a}\vert^2\vert\overrightarrow{b}\vert^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{\left({a_1}^2+{a_2}^2+{a_3}^2\right)\left({b_1}^2+{b_2}^2+{b_3}^2\right)-(a_1b_1+a_2b_2+a_3b_3)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2} \ \end{eqnarray}}\)

三角形の面積の公式

空間ベクトルでも三角形の面積の公式は平面ベクトルで覚えた式と同じ式を利用するから覚えておこう。
数学Ⅰで勉強した三角形の面積の公式の変形でもあるからね。
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{2}|\overrightarrow{\mathrm{AB}}||\overrightarrow{\mathrm{AC}}|\sin\theta \\
&=&\displaystyle\frac{1}{2}|\overrightarrow{\mathrm{AB}}||\overrightarrow{\mathrm{AC}}|\sqrt{1-\cos^2\theta}\\
&=&\displaystyle\frac{1}{2}|\overrightarrow{\mathrm{AB}}||\overrightarrow{\mathrm{AC}}|\sqrt{1-\left(\displaystyle\frac{\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}}{|\overrightarrow{\mathrm{AB}}||\overrightarrow{\mathrm{AC}}|}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{|\overrightarrow{\mathrm{AB}}|^2|\overrightarrow{\mathrm{AC}}|^2-\left(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\right)^2} \ \end{eqnarray}}\)

\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{AB}}\vert^2\vert\overrightarrow{\mathrm{AC}}\vert^2-\left(\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\right)^2} \ }\)
「成分表示でないベクトルの問題」と「成分表示のベクトルの問題」のどちらの場合でもこの公式を利用して解くから確実に覚えておこう。

面積を求めるために必要なもの

面積を求めるって言っても必要な情報がないと求めることが出来ないんだ。

成分表示でない空間ベクトルでは基準のベクトルが\(\small{ \ 3 \ }\)つ必要だったよね。

CHECK
空間ベクトルの基本-i
空間ベクトルの基本

空間ベクトルの表し方などついて詳しく解説しています。

続きを見る

だからこの基準のベクトルの大きさと内積が必要になるんだ。
これがわかってないと面積を求めることが出来ないからね。

基準のベクトルが\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)のとき
必要になるのは
\(\small{ \ \vert\overrightarrow{\mathrm{OA}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OB}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OC}}\vert \ }\)、\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}} \ }\)の\(\small{ \ 6 \ }\)つ。

これさえ分かっていれば、基準のベクトルで表すことの出来る点を結んだ空間中の三角形の面積は求めることができるんだ。

成分表示の問題の場合、三角形の頂点の成分（座標）がわかっていれば、\(\small{ \ 2 \ }\)辺の大きさも内積もわかるから面積を求めることが出来るよね。

成分表示でない三角形の面積

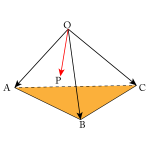
例えば空間中にある\(\small{ \ \triangle\mathrm{PQR} \ }\)の面積\(\small{ \ \mathrm{S} \ }\)を求める場合、
\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{PQ}}\vert^2\vert\overrightarrow{\mathrm{PR}}\vert^2-\left(\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{\mathrm{PR}}\right)^2} \ }\)を計算すればいいんだけど、\(\small{ \ \mathrm{P} \ }\)や\(\small{ \ \mathrm{Q} \ }\)、\(\small{ \ \mathrm{R} \ }\)はどこかの内分点だったりするから、まずは\(\small{ \ \overrightarrow{\mathrm{PQ}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{PR}} \ }\)を基準のベクトルで表す必要がある。

つまり始点が\(\small{ \ \mathrm{O} \ }\)で基準のベクトルが\(\small{ \ \overrightarrow{\mathrm{OA}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OC}} \ }\)だったら、\(\small{ \ \overrightarrow{\mathrm{PQ}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{PR}} \ }\)を\(\small{ \ s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC}} \ }\)の形で表すってこと。

基準のベクトルの\(\small{ \ \vert\overrightarrow{\mathrm{OA}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OB}}\vert \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{OC}}\vert \ }\)、\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}} \ }\)、\(\small{ \ \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}} \ }\)の\(\small{ \ 6 \ }\)つが分かっていると\(\small{ \ \vert\overrightarrow{\mathrm{PQ}\vert} \ }\)、\(\small{ \ \vert\overrightarrow{\mathrm{PR}}\vert \ }\)、\(\small{ \ \overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{\mathrm{PR}} \ }\)をこの\(\small{ \ 6 \ }\)つを利用して計算することが出来るから、計算して\(\small{ \ \mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{PQ}}\vert^2\vert\overrightarrow{\mathrm{PR}}\vert^2-\left(\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{\mathrm{PR}}\right)^2} \ }\)に代入して面積を求めよう。

例題を確認
問題解答

\(\small{ \ 1 \ }\)辺の長さが\(\small{ \ 1 \ }\)の正四面体\(\small{ \ \mathrm{ABCD} \ }\)がある。\(\small{ \ \mathrm{AB} \ }\)の中点を\(\small{ \ \mathrm{P} \ }\)、\(\small{ \ \mathrm{AC} \ }\)を\(\small{ \ 2:1 \ }\)に内分する点を\(\small{ \ \mathrm{Q} \ }\)、\(\small{ \ \mathrm{AD} \ }\)を\(\small{ \ 1:3 \ }\)に内分する点を\(\small{ \ \mathrm{R} \ }\)とするとき、\(\small{ \ \triangle\mathrm{PQR} \ }\)の面積\(\small{ \ \mathrm{S} \ }\)を求めよ。

空間ベクトルと三角形の面積-01

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PQ}}&=&\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AP}}\\
&=&\displaystyle\frac{2}{3}\overrightarrow{\mathrm{AC}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AB}} \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PR}}&=&\overrightarrow{\mathrm{AR}}-\overrightarrow{\mathrm{AP}}\\
&=&\displaystyle\frac{1}{4}\overrightarrow{\mathrm{AD}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AB}} \ \end{eqnarray}}\)
\(\small{ \ 1 \ }\)辺の長さが\(\small{ \ 1 \ }\)の正四面体\(\small{ \ \mathrm{ABCD} \ }\)より
\(\small{ \ \vert\overrightarrow{\mathrm{AB}}\vert=\vert\overrightarrow{\mathrm{AC}}\vert=\vert\overrightarrow{\mathrm{AD}}\vert=1 \ }\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}&=&\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AD}}\\
&=&1\times1\times\cos 60^{\circ}=\displaystyle\frac{1}{2} \ \end{eqnarray}}\)
\(\small{ \ \overrightarrow{\mathrm{PQ}} \ }\)の大きさは

\(\small{\begin{eqnarray} \ \vert\overrightarrow{\mathrm{PQ}}\vert^2&=&\vert\displaystyle\frac{2}{3}\overrightarrow{\mathrm{AC}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AB}}\vert^2\\
&=&\vert\displaystyle\frac{1}{6}\left(4\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}\right)\vert^2\\
&=&\displaystyle\frac{1}{36}\vert4\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}\vert^2\\
&=&\displaystyle\frac{1}{36}\left(16\vert\overrightarrow{\mathrm{AC}}\vert^2-24\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}+9\vert\overrightarrow{\mathrm{AB}}\vert^2\right)\\
&=&\displaystyle\frac{1}{36}(16-12+9)\\
&=&\displaystyle\frac{13}{36} \ \end{eqnarray}}\)

\(\small{ \ \overrightarrow{\mathrm{PR}} \ }\)の大きさは

\(\small{\begin{eqnarray} \ \vert\overrightarrow{\mathrm{PR}}\vert^2&=&\vert\displaystyle\frac{1}{4}\overrightarrow{\mathrm{AD}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AB}}\vert^2\\
&=&\vert\displaystyle\frac{1}{4}\left(\overrightarrow{\mathrm{AD}}-2\overrightarrow{\mathrm{AB}}\right)\vert^2\\
&=&\displaystyle\frac{1}{16}\vert\overrightarrow{\mathrm{AD}}-2\overrightarrow{\mathrm{AB}}\vert^2\\
&=&\displaystyle\frac{1}{16}\left(\vert\overrightarrow{\mathrm{AD}}\vert^2-4\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AD}}+4\vert\overrightarrow{\mathrm{AB}}\vert^2\right)\\
&=&\displaystyle\frac{1}{16}(1-2+4)\\
&=&\displaystyle\frac{3}{16} \ \end{eqnarray}}\)

\(\small{ \ \overrightarrow{\mathrm{PQ}} \ }\)と\(\small{ \ \overrightarrow{\mathrm{PR}} \ }\)の内積は

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{\mathrm{PR}}&=&\left(\displaystyle\frac{2}{3}\overrightarrow{\mathrm{AC}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AB}}\right)\cdot\left(\displaystyle\frac{1}{4}\overrightarrow{\mathrm{AD}}-\displaystyle\frac{1}{2}\overrightarrow{\mathrm{AB}}\right)\\
&=&\displaystyle\frac{1}{6}\left(4\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}\right)\cdot\displaystyle\frac{1}{4}\left(\overrightarrow{\mathrm{AD}}-2\overrightarrow{\mathrm{AB}}\right)\\
&=&\displaystyle\frac{1}{24}\left(4\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}\right)\cdot\left(\overrightarrow{\mathrm{AD}}-2\overrightarrow{\mathrm{AB}}\right)\\
&=&\displaystyle\frac{1}{24}\left(4\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{AD}}-8\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}-3\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AD}}+6\vert\overrightarrow{\mathrm{AB}}\vert^2\right)\\
&=&\displaystyle\frac{1}{24}\left(2-4-\displaystyle\frac{3}{2}+6\right)\\
&=&\displaystyle\frac{5}{48} \ \end{eqnarray}}\)

よって求める面積は

\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{2}\sqrt{\vert\overrightarrow{\mathrm{PQ}}\vert^2\vert\overrightarrow{\mathrm{PR}}\vert^2-\left(\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{\mathrm{PR}}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{\displaystyle\frac{13}{36}\cdot\displaystyle\frac{3}{16}-\left(\displaystyle\frac{5}{48}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{\displaystyle\frac{39\times4-25}{48^2}}\\
&=&\displaystyle\frac{1}{2}\sqrt{\displaystyle\frac{131}{48^2}}\\
&=&\displaystyle\frac{\sqrt{131}}{96} \ \end{eqnarray}}\)

point
係数が分数のベクトルの大きさや内積を計算するのって大変だよね。

だから分数が係数のベクトルは一度係数を通分してくくりだして計算することで、分数のまま計算するよりも簡単に計算することができる。

計算量も減るし、計算ミスも防ぐことができるから覚えておこう。

ちなみにこの例題はベクトルを使わなくても余弦定理を利用して\(\small{ \ \mathrm{PQ} \ }\)、\(\small{ \ \mathrm{QR} \ }\)、\(\small{ \ \mathrm{PR} \ }\)を求めて、さらに\(\small{ \ 3 \ }\)辺の長さから面積を求めることもできる。

だけど下図のような面積だと三角比だけで求めるのはなかなか難しいからベクトルを利用して求めよう。
空間ベクトルと三角形の面積-02

CHECK
三角形の面積-i
三角形の面積

ヘロンの公式や内接円の半径の求め方について詳しく解説しています。

続きを見る

成分表示の三角形の面積

成分表示の場合は、求める三角形の\(\small{ \ 2 \ }\)辺のベクトルを成分で表わそう。

成分がわかったら、大きさや内積を求めて三角形の面積の公式に代入していこう。
\(\small{ \ \overrightarrow{a}=(a_1, \ a_2, \ a_3) \ }\)
\(\small{ \ \overrightarrow{b}=(b_1, \ b_2, \ b_3) \ }\)
\(\small{ \ \overrightarrow{a} \ }\)、\(\small{ \ \overrightarrow{b} \ }\)の作る三角形の面積\(\small{ \ \mathrm{S} \ }\)は

\(\small{\mathrm{S}=\displaystyle\frac{1}{2}\sqrt{\left({a_1}^2+{a_2}^2+{a_3}^2\right)\left({b_1}^2+{b_2}^2+{b_3}^2\right)-(a_1b_1+a_2b_2+a_3b_3)^2} \ }\)

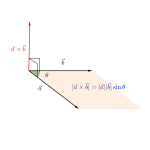
ちなみに外積の大きさは三角形の面積の\(\small{ \ 2 \ }\)倍の値になるから、それを利用して

\(\small{\mathrm{S}=\displaystyle\frac{1}{2}\sqrt{(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2} \ }\)

ってすることも出来るからね。

CHECK
外積-i
空間ベクトルと外積

外積の計算や性質について詳しく解説しています。

続きを見る

例題を確認
問題解答

\(\small{ \ \mathrm{A}(1,\ 2, \ 3) \ }\)、\(\small{ \ \mathrm{B}(2,\ -1, \ 1) \ }\)、\(\small{ \ \mathrm{C}(-1,\ 3, \ -2) \ }\)のとき、\(\small{ \ \triangle \mathrm{ABC} \ }\)の面積\(\small{ \ \mathrm{S} \ }\)を求めよ。

\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AB}}&=&(2,\ -1, \ 1)-(1, \ 2, \ 3)\\
&=&(1, \ -3, \ -2) \ \end{eqnarray}}\)
\(\small{\begin{eqnarray} \ \overrightarrow{\mathrm{AC}}&=&(-1,\ 3, \ -2)-(1, \ 2, \ 3)\\
&=&(-2, \ 1, \ -5) \ \end{eqnarray}}\)
\(\small{ \ \vert \overrightarrow{\mathrm{AB}}\vert=\sqrt{1^2+(-3)^2+(-2)^2}=\sqrt{14} \ }\)
\(\small{ \ \vert \overrightarrow{\mathrm{AC}}\vert=\sqrt{(-2)^2+1^2+(-5)^2}=\sqrt{30} \ }\)
\(\small{ \ \overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=-2-3+10=-5 \ }\)
\(\small{\begin{eqnarray} \ \mathrm{S}&=&\displaystyle\frac{1}{2}\sqrt{\vert \overrightarrow{\mathrm{AB}}\vert^2 \vert \overrightarrow{\mathrm{AC}}\vert^2- \left(\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}\right)^2}\\
&=&\displaystyle\frac{1}{2}\sqrt{14\times30-(-5)^2}\\
&=&\displaystyle\frac{\sqrt{395}}{2} \ \end{eqnarray}}\)

Point 空間ベクトルと三角形の面積

①ベクトルの三角形の面積の公式を覚える
②成分表示された問題とされてない問題の解き方をマスターする

この記事が気に入ったら
いいね ! しよう

シェアする
ツイートする
Twitter で

-空間ベクトル

-,

  • この記事を書いた人
  • 最新記事

リンス

名前：リンス
職業：塾講師/家庭教師
性別：男
趣味：料理・問題研究
好物：ビール・BBQ