複素数の極形式と乗法・除法

こんにちは、リンス(@Lins016)です。
今回は複素数の極形式と乗法・除法について学習していこう。

極形式

複素数では\(\small{ \ z=a+bi \ }\)の標準形と\(\small{ \ z=r(\cos \theta+i\sin \theta) \ }\)の極形式の表し方がよく使われる。今回はこの\(\small{ \ z=r(\cos \theta+i\sin \theta) \ }\)への変形と極形式を利用して、複素数の積や商が複素数平面上でどのような図形を描くのか考えてみよう。

極形式への変形

\(\small{ \ z=a+bi \ }\)の標準形を\(\small{ \ z=r(\cos \theta+i\sin \theta) \ }\)の極形式に変形する方法を覚えよう。

これは図を見れば明らかなんだけど、\(\small{ \ |z|=\sqrt{a^2+b^2}=r \ }\)として、\(\small{ \ x \ }\)軸と\(\small{ \ \mathrm{OP} \ }\)のなす角を\(\small{ \ \theta \ }\)とすれば、\(\small{ \ a=r\cos \theta, \ b=r\sin \theta \ }\)が言えるよね。

だから\(\small{ \ z=r(\cos \theta+i\sin \theta) \ }\)が言えるんだ。

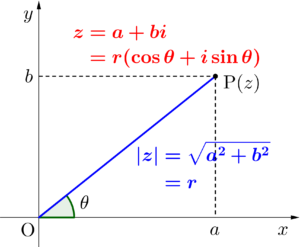
そして極形式への変形のやり方だけど、それは次の手順でやっていこう。
①まずは実部と虚部の二乗の和の平方根でくくりだそう。
\(\small{\begin{eqnarray} \ z&=&a+bi\\[3pt] &=&\sqrt{a^2+b^2}\left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}+\displaystyle\frac{b}{\sqrt{a^2+b^2}}i\right) \ \end{eqnarray}}\)

②くくりだしたことによって括弧内の実部と虚部の二乗の和を考えると
\(\small{ \ \left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\displaystyle\frac{b}{\sqrt{a^2+b^2}}\right)^2=1 \ }\)になるから\(\small{ \ \displaystyle\frac{a}{\sqrt{a^2+b^2}}=\cos\theta, \ \displaystyle\frac{b}{\sqrt{a^2+b^2}}=\sin\theta \ }\)とおける。
これを満たす\(\small{ \ \theta \ }\)を見つけよう。
\(\small{\begin{eqnarray} \ z&=&a+bi\\[3pt] &=&\sqrt{a^2+b^2}\left(\displaystyle\frac{a}{\sqrt{a^2+b^2}}+\displaystyle\frac{b}{\sqrt{a^2+b^2}}i\right)\\[3pt] &=&\sqrt{a^2+b^2}(\cos\theta+i\sin\theta)\\[3pt] &=&r(\cos\theta+i\sin\theta) \ \end{eqnarray}}\)

ちなみにこの\(\small{ \ \theta \ }\)のことを偏角って言って、\(\small{ \ \theta=\mathrm{arg} \ z \ }\)って書く。これは「\(\small{ \ z \ }\)を極形式で書くとその偏角は\(\small{ \ \theta \ }\)です。」って意味になるから覚えておこう。

\(\small{ \ \mathrm{arg} \ }\)は偏角を表す\(\small{ \ \mathrm{argument} \ }\)(アーギュメント)の略で「\(\small{ \ \mathrm{arg} \ z \ }\)」を「アーギュメント　ゼット」や「アーグ　ゼット」って読む。

\(\small{ \ a+bi \ }\)を極形式に変形するとき偏角が有名角（三角比の値を知っている角度のこと）になるためには\(\small{ \ a:b \ }\)が\(\small{ \ 1:1, \ \sqrt{3}:1, \ 1:\sqrt{3}, \ 1:0, \ 0:1 \ }\)にプラスかマイナスがついた形の比になってないと有名角にはならないから覚えておこう。

複素数の積

\(\small{ \ z_1=a+bi, \ z_2=c+di \ }\)のとき、
\(\small{\begin{eqnarray}z_1z_2&=&(a+bi)(c+di)\\[3pt] &=&ac-bd+(ad+bc)i \ \end{eqnarray}}\)
になるよね。
でもこれって式の計算だけで、複素数平面上での動きってわかりづらいよね。
調べてみると
\(\small{\begin{eqnarray}|z_1z_2|^2&=&(ac-bd)^2+(ad+bc)^2\\[3pt] &=&a^2c^2+b^2d^2+a^2d^2+b^2c^2\\[3pt] &=&a^2(c^2+d^2)+b^2(c^2+d^2)\\[3pt] &=&(a^2+b^2)(c^2+d^2)\\[3pt] &=&|z_1|^2|z_2|^2 \ \end{eqnarray}}\)
\(\small{ \ \therefore |z_1z_2|=|z_1||z_2| \ }\)
がわかるよね。

これを極形式で考えてみよう。
\(\small{ \ z_1=r_1(\cos \theta_1+i\sin \theta_1) \ }\)
\(\small{ \ z_2=r_2(\cos \theta_2+i\sin \theta_2) \ }\)
とすると、

これは\(\small{ \ z_1z_2 \ }\)が\(\small{ \ |z_1z_2|=r_1r_2 \ }\)、偏角\(\small{ \ \theta_1+\theta_2 \ }\)の複素数を表してることになるんだ。

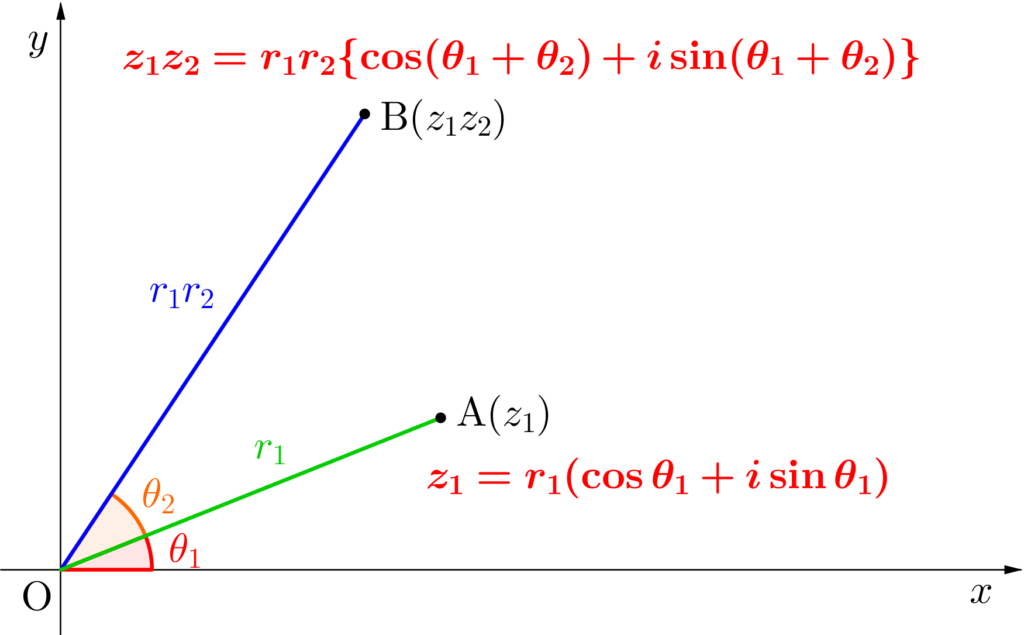
これって複素数平面上では、点\(\small{ \ \mathrm{A}(z_1) \ }\)を原点を中心に\(\small{ \ \theta_2 \ }\)回転させて、原点からの距離を\(\small{ \ r_2 \ }\)倍拡大（または縮小）したものになるよね。

ちなみに

は加法定理による変形だからね。

このことから
\(\small{ \ z_1=r_1(\cos \theta_1+i\sin \theta_1) \ }\)
（\(\small{ \ |z_1|=r_1, \ \mathrm{arg} \ z_1=\theta_1 \ }\)）
\(\small{ \ z_2=r_2(\cos \theta_2+i\sin \theta_2) \ }\)
（\(\small{ \ |z_2|=r_2, \ \mathrm{arg} \ z_2=\theta_2 \ }\)）のとき

\(\small{ \ z_1z_2=r_1r_2\left\{\cos(\theta_1+\theta_2)+i\sin (\theta_1+\theta_2)\right\} \ }\)
\(\small{ \ |z_1z_2|=r_1r_2=|z_1||z_2| \ }\)
\(\small{ \ \mathrm{arg} \ z_1z_2=\theta_1+\theta_2=\mathrm{arg} \ z_1+\mathrm{arg} \ z_2 \ }\)
が言えるんだ。

特に\(\small{ \ r_2=1 \ }\)のとき\(\small{ \ z_1z_2 \ }\)は\(\small{ \ z_1 \ }\)を原点を中心に\(\small{ \ \theta_2 \ }\)回転移動した点ってことになるからね。

複素数の商

複素数の商は極形式を使うと分かりやすい。
\(\small{ \ z_1=r_1(\cos \theta_1+i\sin \theta_1) \ }\)
\(\small{ \ z_2=r_2(\cos \theta_2+i\sin \theta_2) \ }\)のとき
\(\small{ \ \displaystyle\frac{z_1}{z_2} \ }\)を考えてみよう。

これは\(\small{ \ \displaystyle\frac{z_1}{z_2} \ }\)が\(\small{ \ \left|\displaystyle\frac{z_1}{z_2}\right|=\displaystyle\frac{r_1}{r_2} \ }\)、偏角\(\small{ \ \theta_1-\theta_2 \ }\)の複素数を表してることになるんだ。

これって複素数平面上では、点\(\small{ \ \mathrm{A}(z_1) \ }\)を原点を中心に\(\small{ \ -\theta_2 \ }\)回転させて、原点からの距離を\(\small{ \ \displaystyle\frac{1}{r_2} \ }\)倍縮小（または拡大）したものになるよね。

このことから
\(\small{ \ z_1=r_1(\cos \theta_1+i\sin \theta_1) \ }\)
（\(\small{ \ |z_1|=r_1, \ \mathrm{arg} \ z_1=\theta_1 \ }\)）
\(\small{ \ z_2=r_2(\cos \theta_2+i\sin \theta_2) \ }\)
（\(\small{ \ |z_2|=r_2, \ \mathrm{arg} \ z_2=\theta_2 \ }\)）のとき

\(\small{ \ \displaystyle\frac{z_1}{z_2}=\displaystyle\frac{r_1}{r_2}\left\{\cos(\theta_1-\theta_2)+i\sin (\theta_1-\theta_2)\right\} \ }\)
\(\small{ \ \left|\displaystyle\frac{z_1}{z_2}\right|=\displaystyle\frac{r_1}{r_2}=\displaystyle\frac{|z_1|}{|z_2|} \ }\)
\(\small{ \ \mathrm{arg} \ \displaystyle\frac{z_1}{z_2}=\theta_1-\theta_2=\mathrm{arg} \ z_1-\mathrm{arg} \ z_2 \ }\)
が言えるんだ。

問題解答

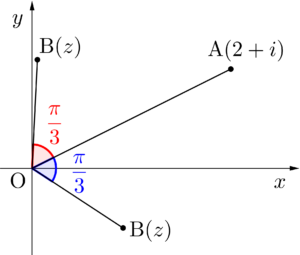
\(\small{ \ 3 \ }\)点\(\small{ \ \mathrm{O}(0) \ }\)と\(\small{ \ \mathrm{A}(2+i) \ }\)と\(\small{ \ \mathrm{B} \ }\)が\(\small{ \ \mathrm{OA}=2\mathrm{OB} \ }\)かつ\(\small{ \ \angle \mathrm{AOB}=\displaystyle\frac{\pi}{3} \ }\)を満たしているとき、点\(\small{ \ \mathrm{B} \ }\)を表す複素数を求めよ。

点\(\small{ \ \mathrm{B}(z) \ }\)とすると

(i)反時計回りに回転
\(\small{\begin{eqnarray} \ z&=&(2+i)\displaystyle\frac{1}{2}\left(\cos \displaystyle\frac{\pi}{3}+i\sin \displaystyle\frac{\pi}{3}\right)\\[3pt] &=&(2+i)\left(\displaystyle\frac{1}{4}+ \displaystyle\frac{\sqrt{3}}{4}i\right)\\[3pt] &=&\displaystyle\frac{2-\sqrt{3}}{4}+ \displaystyle\frac{1+2\sqrt{3}}{4}i \ \end{eqnarray}}\)
(ii)時計回りに回転
\(\small{\begin{eqnarray} \ z&=&(2+i)\displaystyle\frac{1}{2}\left\{\cos \left(-\displaystyle\frac{\pi}{3}\right)+i\sin \left(-\displaystyle\frac{\pi}{3}\right\}\right)\\[3pt] &=&(2+i)\left(\displaystyle\frac{1}{4}-\displaystyle\frac{\sqrt{3}}{4}i\right)\\[3pt] &=&\displaystyle\frac{2+\sqrt{3}}{4}+ \displaystyle\frac{1-2\sqrt{3}}{4}i \ \end{eqnarray}}\)

ちなみに\(\small{ \ z=\cos\theta+i\sin\theta \ }\)のとき

\(\small{\begin{eqnarray} \ \displaystyle\frac{1}{z}&=&\displaystyle\frac{1}{(\cos \theta+i\sin \theta)}\\[3pt] &=&\displaystyle\frac{\cos \theta-i\sin \theta}{(\cos \theta+i\sin \theta)(\cos \theta-i\sin \theta)}\\[3pt] &=&\displaystyle\frac{\cos \theta-i\sin \theta}{\cos^2\theta+\sin^2\theta }\\[3pt] &=&\cos \theta-i\sin \theta\\[3pt] &=&\cos (-\theta)+i\sin (-\theta) \ \end{eqnarray}}\)

つまり\(\small{ \ z=\cos\theta+i\sin\theta \ }\)で割るっていうのは\(\small{ \ \displaystyle\frac{1}{z} \ }\)をかけるってことと同じで、これは極形式から原点まわりに\(\small{ \ -\theta \ }\)回転させるっていうのがわかるよね。

ちなみに\(\small{ \ \cos \theta-i\sin \theta \ }\)は虚部の前の符号がマイナスになってるから極形式じゃないんだ。この場合は\(\small{ \ \cos (-\theta)+i\sin (-\theta) \ }\)って変形して極形式にしよう。

Point 複素数の極形式と乗法・除法

①極形式の変形をマスターする
②反時計回りは掛け算
③時計回りは割り算

問題解答

\(\small{ \ \alpha, \ \beta \ }\)は等式\(\small{ \ 3\alpha^2-6\alpha\beta+4\beta^2=0 \ }\)を満たす\(\small{ \ 0 \ }\)でない複素数とする。次の問いに答えよ。
(1)複素数\(\small{ \ \displaystyle\frac{\alpha}{\beta} \ }\)を極形式で表せ。
(2)複素数平面上で複素数\(\small{ \ 0, \ \alpha, \ \beta \ }\)を表す点をそれぞれ\(\small{ \ \mathrm{O, \ A, \ B} \ }\)とするとき、\(\small{ \ \angle \mathrm{AOB} \ }\)および\(\small{ \ \angle \mathrm{OAB} \ }\)を求めよ。

(1)
\(\small{ \ 3\alpha^2-6\alpha\beta+4\beta^2=0 \ }\)より
両辺を\(\small{ \ \beta^2 \ }\)で割って
\(\small{ \ 3\left(\displaystyle\frac{\alpha}{\beta}\right)^2-6\left(\displaystyle\frac{\alpha}{\beta}\right)+4=0 \ }\)
\(\small{ \ t=\displaystyle\frac{\alpha}{\beta} \ }\)とする
\(\small{ \ 3t^2-6t+4=0 \ }\)
\(\small{\begin{eqnarray} \ t&=&\displaystyle\frac{3\pm \sqrt{9-12}}{3}\\[3pt] &=&\displaystyle\frac{3\pm \sqrt{3}i}{3}\\[3pt] &=&\displaystyle\frac{2\sqrt{3}}{3}\left(\displaystyle\frac{\sqrt{3}}{2}\pm \displaystyle\frac{1}{2}i\right)\\[3pt] &=&\displaystyle\frac{2\sqrt{3}}{3}\left\{\cos \left(\pm\displaystyle\frac{\pi}{6}\right)+i \sin \left(\pm\displaystyle\frac{\pi}{6}\right)\right\} \ \end{eqnarray}}\)
\(\small{ \ \therefore \displaystyle\frac{\alpha}{\beta}=\displaystyle\frac{2\sqrt{3}}{3}\left\{\cos \left(\pm\displaystyle\frac{\pi}{6}\right)+i \sin \left(\displaystyle\frac{\pi}{6}\right)\right\} \ }\)

(2)

(1)より
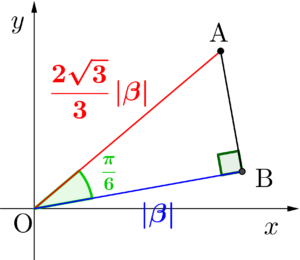
\(\small{ \ \angle \mathrm{AOB}=\displaystyle\frac{\pi}{6} \ }\)
また、\(\small{ \ \mathrm{OA:OB}=2:\sqrt{3} \ }\)かつ\(\small{ \ \angle \mathrm{AOB}=\displaystyle\frac{\pi}{6} \ }\)より\(\small{ \ \triangle\mathrm{OAB} \ }\)は直角三角形である
\(\small{ \ \angle \mathrm{OAB}=\displaystyle\frac{\pi}{3} \ }\)