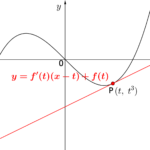こんにちは、リンス(@Lins016)です。
今回は三次関数のグラフと面積について学習していこう。
三次関数のグラフと面積
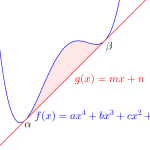
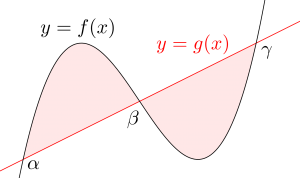
三次関数と直線や放物線で囲まれた面積を求める場合、どちらの関数が上側にあるのか考えて求めよう。
また以前学習した三次関数のグラフの対称性も頭に入れておこう。いざって時に使えるからね。
\(\small{\mathrm{S}=\displaystyle\int_{\alpha}^{\beta}\left\{f(x)-g(x)\right\}+\displaystyle\int_{\beta}^{\gamma}\left\{g(x)-f(x)\right\}}\)
三次関数とx軸で囲まれた面積
三次関数と\(\small{ \ x \ }\)軸で囲まれた面積を求める場合、まずは\(\small{ \ x \ }\)軸との交点を求めよう。
交点の数が三つあれば囲まれる面積は二つあるし、交点が二つの場合は囲まれる面積は一つになるからね。
次にグラフが\(\small{ \ x \ }\)軸より上側にあるか、下側にあるかを考えよう。これは三次関数のグラフの形状(\(\small{ \ x^3 \ }\))の係数が「正か負か」と\(\small{ \ x \ }\)軸との交点の個数と座標で判断しよう。
面積を求めるのに必要なのは「積分区間(\(\small{ \ x \ }\)軸との交点の\(\small{ \ x \ }\)座標)」と「グラフが\(\small{ \ x \ }\)軸より上側にあるか、下側にあるか」のこの二つだけなんだ。
よく三次関数のグラフの極値を求めようと微分する人がいるけど、面積を求めるだけなら極値は必要ないからね。
もちろんわかってるに越したことはないけど、特別必要ないし、それを求める時間がもったいないよね。
\(\small{ \ y=x^3-x \ }\)と\(\small{ \ x \ }\)軸で囲まれた面積を求めよ。
グラフと\(\small{ \ x \ }\)軸との交点の\(\small{ \ x \ }\)座標は
\(\small{ \ x^3-x=0 \ }\)
\(\small{ \ x(x-1)(x+1)=0 \ }\)
\(\small{ \ \therefore x=-1, \ 0, \ 1 \ }\)
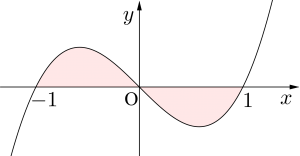
よって求める面積は
\(\small{ \ \displaystyle \int_{-1 }^{0} (x^3-x) dx+\displaystyle \int_{0}^{1} -(x^3-x) dx\\
=\left[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{1}{2}x^2\right]_{-1}^{0}+\left[-\displaystyle\frac{1}{4}x^4+\displaystyle\frac{1}{2}x^2\right]_{0}^{1}\\
=\displaystyle\frac{1}{2} \ }\)

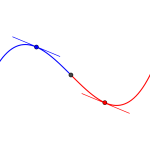
三次関数とその接線で囲まれた面積
次に三次関数とその接線で囲まれた面積について考えていこう。
まずは三次関数の接線を求めよう。
\(\small{ \ y=f(x) \ }\)の\(\small{ \ (t, \ f(t) \ ) \ }\)における接線の方程式は
\(\small{ \ y=f'(t)(x-t)+f(t) \ }\)だったよね。これは公式っていうぐらい大切な式だから確実に覚えておこう。
-

接線の方程式
曲線上の点における接線の求め方や曲線上にない点から引いた接線の方程式の求め方について解説しています。
続きを見る
接線が求まったら、接点以外の接線と三次関数の共有点を求めよう。
このとき方程式\(\small{ \ f(x)=f'(t)(x-t)+f(t) \ }\)を解くんだけど、\(\small{ \ x=t \ }\)は接点だから、この方程式の解に\(\small{ \ x=t \ }\)があるのがわかるよね。
さらに\(\small{ \ x=t \ }\)は接点だから重解になるはず。
だから方程式\(\small{ \ f(x)=f'(t)(x-t)+f(t) \ }\)は\(\small{ \ (x-t)^2(x-\alpha)=0 \ }\)の形に式変形できるんだ。
三次関数のグラフと直線の交点の数で方程式の解の個数が変わるからね。
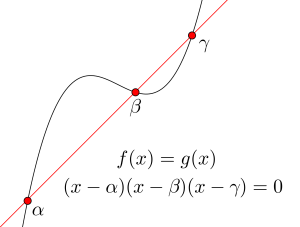
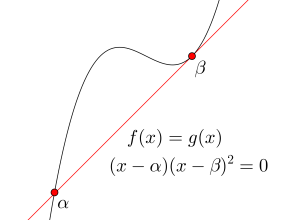
交点の\(\small{ \ x \ }\)座標を求めたら、接線とグラフの位置関係を調べよう。
接線と三次関数のグラフの位置関係を調べるには積分区間内の適当な数値を代入してどっちが上にあるか調べてもいいけど、一番簡単なのは三次関数を二回微分して、接点の\(\small{ \ x \ }\)座標\(\small{ \ t \ }\)を代入しよう。
この値が正ならグラフは下に凸になるから、三次関数の方が接線より上にある。この値が負ならグラフは上に凸になるから三次関数の方が接線より下にあることになるからね。
-

三次関数の対称性と変曲点
変曲点や変曲点を利用する問題について詳しく解説しています。
続きを見る
グラフの位置関係がわかったら面積を求めよう。共有点を積分区間に設定して、上の線から下の線を引いた関数を積分することで面積が求まるからね。
\(\small{ \ y=x^3-x \ }\)上の点\(\small{ \ (1, \ 0) \ }\)における接線とこの曲線で囲まれた面積を求めよ。
\(\small{ \ f(x)=x^3-x \ }\)とすると接線の方程式は
\(\small{\begin{eqnarray} \ f(x)&=&f'(1)(x-1)+f(1)\\
&=&2x-2 \ \end{eqnarray}}\)
接線と曲線の交点\(\small{ \ x \ }\)座標は
\(\small{ \ x^3-x=2x-2 \ }\)
\(\small{ \ x^3-3x+2=0 \ }\)
\(\small{ \ (x-1)^2(x+2)=0 \ }\)
\(\small{ \ \therefore x=1, \ -2 \ }\)
よって求める面積は
\(\small{ \ \displaystyle \int_{-2}^{1} \left\{(x^3-x)-(2x-2)\right\}dx\\
=\displaystyle \int_{-2}^{1}(x^3-3x+2) dx\\
=\left[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{3}{2}x^2+2x\right]_{-2}^{1}\\
=\displaystyle\frac{27}{4} \ }\)
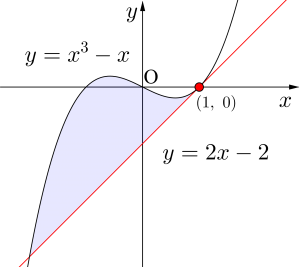

この解答では面積を求めるときそのまま計算したけど、接線と曲線で囲まれた面積は\(\small{ \ \displaystyle \int_{\alpha}^{\beta} (x-\alpha)(x-\beta)^2 dx \ }\)の形になるから
を利用しても構わないからね。
-

第一種オイラー積分・ベータ関数の証明とその利用
第一種オイラー積分の証明から面積の公式の利用について解説しています。
続きを見る
Point 定積分の計算と面積
①グラフの形状と直線の位置関係を確認する
②積分区間を求める
③面積は上の線引く下の線を積分する
\(\small{ \ y=x^3-6x^2+9x \ }\)と\(\small{ \ y=ax \ }\)で囲まれた二つの面積が等しいとき\(\small{ \ a \ }\)の値を求めよ。ただし、\(\small{ \ 0\lt a \lt 9 \ }\)とする。
\(\small{ \ x^3-6x^2+9x=ax \ }\)
\(\small{ \ x\left\{x^2-6x+(9-a)\right\}=0 \ }\)
この方程式の解を
\(\small{ \ x=0, \ \alpha, \ \beta(\alpha \lt \beta) \ }\)とすると
二つの面積は
\(\small{ \ \mathrm{S_1}=\displaystyle\int_{0}^{\alpha}\left\{x^3-6x^2+(9-a)x\right\} \ }\)
\(\small{ \ \mathrm{S_2}=\displaystyle\int_{\alpha}^{\beta}\left\{-x^3+6x^2-(9-a)x\right\} \ }\)
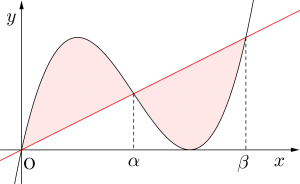
この二つの面積が等しいので
\(\small{ \ \mathrm{S_1}=\mathrm{S_2} \ }\)
\displaystyle\int_{0}^{\alpha}\left\{x^3-6x^2+(9-a)x\right\}-\displaystyle\int_{\alpha}^{\beta}\left\{-x^3+6x^2-(9-a)x\right\}=0\\
\displaystyle\int_{0}^{\alpha}\left\{x^3-6x^2+(9-a)x\right\}+\displaystyle\int_{\alpha}^{\beta}\left\{x^3-6x^2+(9-a)x\right\}=0 \ }\)
\(\small{ \ \displaystyle\int_{0}^{\beta}\left\{x^3-6x^2+(9-a)x\right\}=0 \ }\)
\(\small{ \ \left[\displaystyle\frac{1}{4}x^4-2x^3+\displaystyle\frac{9-a}{2}x^2\right]_{0}^{\beta}=0 \ }\)
\(\small{ \ \displaystyle\frac{1}{4}\beta^4-2\beta^3+\displaystyle\frac{9-a}{2}\beta^2=0 \ }\)
\(\small{ \ \beta \neq 0 \ }\)より
\(\small{ \ \beta^2-8\beta+2(9-a)=0\cdots① \ }\)
ここで\(\small{ \ \beta \ }\)は\(\small{ \ x^2-6x+(9-a)=0 \ }\)の大きいほうの解より
\(\small{ \ \beta=3+\sqrt{a} \ }\)
\(\small{ \ a=(\beta-3)^2 \ }\)を\(\small{ ① }\)に代入して
\(\small{ \ \beta^2-8\beta+18-2(\beta-3)^2=0 \ }\)
\(\small{ \ -\beta(\beta-4)=0 \ }\)
\(\small{ \ \beta\neq0 \ }\)より\(\small{ \ \beta=4 \ }\)
\(\small{ \ \therefore a=1 \ }\)

今回はきちんと計算立てて解いたけど、三次関数のグラフは変曲点について対称だから変曲点を通るときがその答えになるよね。変曲点は数学Ⅲで教わる内容だけど、知っておくと便利だから、覚えておこう。