こんにちは、リンス(@Lins016)です。
今回は対数関数を含む方程式・不等式と領域について学習していこう。
対数関数を含む方程式・不等式と領域
本来「不等式と領域」は数学Ⅱの「図形と方程式」で学習する範囲だけど、対数関数でも領域を図示する問題ってあるんだ。
対数関数が試験範囲の中間テストや期末テストにはそう出題されることはないかもしれないけど、実力テストや入試には出題されるから確実に押さえておこう。
その前にまずは「不等式と領域」を再度確認しておこう。
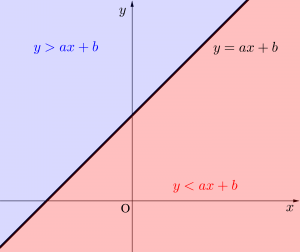
図示の問題
「次の条件を満たす点\(\small{ \ \left(x, \ y\right) \ }\)を図示せよ。」って問題があるよね。
図示せよってことで図を書くことに注目しがちだけど、図を書く前に\(\small{ \ x, \ y \ }\)の関係式を求めることが重要なんだ。
\(\small{ \ x, \ y \ }\)の関係式が等式なら円や直線、放物線といった図形になるし、関係式が不等式なら領域になるからね。
つまり「図示せよ」って問題は「関係式を求めよ」って言ってるのと同じだからね。
対数関数を含む方程式・不等式
以前学習した対数関数を含む方程式・不等式の解き方では\(\small{ \ x=2 \ }\)や\(\small{ \ x\leqq2 \ }\)のように\(\small{ \ x \ }\)の値や範囲を求めるものだったけど、今回は\(\small{ \ x \ }\)だけじゃなくて\(\small{ \ y \ }\)も含めた方程式・不等式になっているから\(\small{ \ x+y=2 \ }\)や\(\small{ \ x+y\leqq2 \ }\)のような関係式ができる。
この関係式を図示すればいいんだ。
図示するとき必ず境界線について言及しよう。図を見ただけじゃ境界線上の点が含まれるのか含まれないのかわからないからね。
注意する点
対数関数を含む方程式・不等式のままだと図示できないから、対数を含まない形にしないといけない。つまり\(\small{ \ \log_af(x, \ y)\geqq \log_ag(x, \ y) \ }\)のような形を\(\small{ \ f(x, \ y)\geqq g(x, \ y) \ }\)にするってこと。
このとき注意しないといけないのが、底の大きさ。不等式の場合、底の大きさによって不等号の向きが変化するんだったよね。特に底が\(\small{ \ x \ }\)や\(\small{ \ y \ }\)の場合は、\(\small{ \ 1 \ }\)より大きい・小さいで場合分けが必要になるからね。
もちろん真数条件も必要だから忘れないようにしよう。
あと忘れがちなのが対数の底は正かつ\(\small{ \ 1 \ }\)じゃないってこと。忘れないように注意しよう。
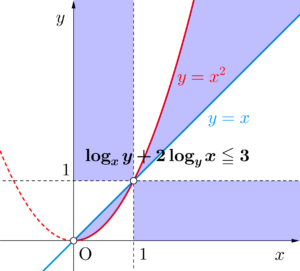
次の不等式を表す領域を図示せよ。
\(\small{ \ \log_xy+2\log_yx\leqq3 \ }\)
真数と底の条件より
\(\small{ \ 0\lt x \lt 1, \ x\gt1 \ }\)
\(\small{ \ 0\lt y \lt 1, \ y\gt1 \ }\)
\(\small{ \ \log_xy=t \ }\)とすると\(\small{ \ \log_yx=\displaystyle\frac{1}{\log_xy}=\displaystyle\frac{1}{t} \ }\)
\(\small{ \ \log_xy+2\log_yx\leqq3 \ }\)
\(\small{ \ t+\displaystyle\frac{2}{t}\leqq3 \ }\)
両辺\(\small{ \ t^2 \ }\)倍すると
\(\small{ \ t^3+2\leqq 3t^2 \ }\)
\(\small{ \ t(t-1)(t-2)\leqq0 \ }\)
\(\small{ \ t\leqq0, \ 1\leqq t\leqq2 \ }\)
\(\small{ \ \log_xy\leqq0, \ 1\leqq \log_xy\leqq2 \ }\)
\(\small{ \ \log_xy\leqq\log_x1, \ \log_xx\leqq \log_xy\leqq\log_xx^2 \ }\)
(i)\(\small{ \ 0\lt x \lt 1 \ }\)のとき
\(\small{ \ y\geqq1, \ x^2\leqq y \leqq x \ }\)
(ii)\(\small{ \ x \gt 1 \ }\)のとき
\(\small{ \ y\leqq1, \ x\leqq y \leqq x^2 \ }\)
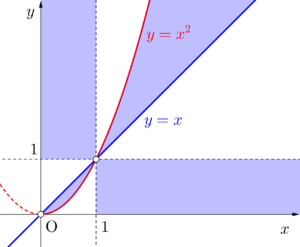
上図の色の部分
ただし、境界線のうち\(\small{ \ x=0, \ x=1, \ y=0, \ y=1 \ }\)は除く

\(\small{ \ t \ }\)の値(正負)で場合分けして、さらに底の大きさでも場合分けすると大変だから場合分けしなくていいように\(\small{ \ t^2 \ }\)倍してるんだ。\(\small{ \ t^2 \ }\)は正の数だから不等号の向きが変わらないからね。
Point 対数関数を含む方程式・不等式と領域
①図示の問題は図を考える前にまずは関係式を導く
②定義域に注意して関係式をきれいに整理する
(1)不等式\(\small{ \ \log_xy-\log_yx^3-2\lt0 \ }\)を満たす点\(\small{ \ (x, \ y) \ }\)が存在する範囲を図示せよ。
(2)連立方程式\(\small{ \ \log_xy-\log_yx^3-2=0, \ x-y+k=0 \ }\)の解の個数が、\(\small{ \ k \ }\)の値によりどう変わるか調べよ。
(1)真数と底の条件より
\(\small{ \ 0\lt x \lt 1, \ x\gt1 \ }\)
\(\small{ \ 0\lt y \lt 1, \ y\gt1 \ }\)
\(\small{ \ \log_xy=t \ }\)とすると
\(\small{ \ \log_yx^3=\displaystyle\frac{3}{\log_xy}=\displaystyle\frac{3}{t} \ }\)
\(\small{ \ \log_xy-\log_yx^3-2\lt0 \ }\)
\(\small{ \ t-\displaystyle\frac{3}{t}-2\lt0 \ }\)
両辺に\(\small{ \ t^2 \ }\)をかけて
\(\small{ \ t^3-2t^2-3t\lt0 \ }\)
\(\small{ \ t(t+1)(t-3)\lt0 \ }\)
\(\small{ \ t\lt-1, \ 0 \lt t \lt 3 \ }\)
\(\small{ \ \log_xy\lt-1, \ 0 \lt \log_xy \lt 3 \ }\)
\(\small{ \ \log_xy\lt-1, \ 0 \lt \log_xy \lt 3 \ }\)
\(\small{ \ \log_xy\lt\log_x\displaystyle\frac{1}{x}, \ \log_x1 \lt \log_xy \lt \log_xx^3 \ }\)
(i)\(\small{ \ 0 \lt x \lt1 \ }\)のとき
\(\small{ \ y\gt\displaystyle\frac{1}{x} \ }\)または\(\small{ \ x^3\lt y \lt1 \ }\)
(ii)\(\small{ \ x \gt1 \ }\)のとき
\(\small{ \ y\lt\displaystyle\frac{1}{x} \ }\)または\(\small{ \ 1\lt y \lt x^3 \ }\)
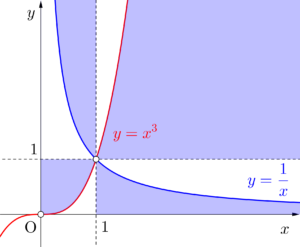
ただし境界線は含まない
(2)\(\small{ \ \log_xy-\log_yx^3-2=0 \ }\)を解くと
\(\small{ \ y=\displaystyle\frac{1}{x}, \ y=x^3 \ }\)
\(\small{ \ xy \ }\)平面に図示したこれらの曲線と\(\small{ \ x-y+k=0 \ }\)の共有点を考える
\(\small{ \ x-y+k=0\Leftrightarrow y=x+k \ }\)
この直線の傾きは\(\small{ \ 1 \ }\)である
この直線と\(\small{ \ y=x^3 \ }\) が接するとき、接点の座標を\(\small{ \ a \ }\)とすると、\(\small{ \ x=a \ }\)における接線の傾きは
\(\small{ \ y'=3a^2 \ }\)
\(\small{ \ 3a^2=1 \ }\)より\(\small{ \ a=\displaystyle\frac{\sqrt{3}}{3} \ (a\gt0) \ }\)
よって接点の座標は\(\small{ \ \left(\displaystyle\frac{\sqrt{3}}{3}, \ \displaystyle\frac{\sqrt{3}}{9}\right) \ }\)
このとき\(\small{ \ k=\displaystyle\frac{\sqrt{3}}{9}-\displaystyle\frac{\sqrt{3}}{3}0=-\displaystyle\frac{2\sqrt{3}}{9} \ }\)
また\(\small{ \ y=x+k \ }\)が\(\small{ \ (x, \ y)=(1, \ 1) \ }\)を通るとき\(\small{ \ k=0 \ }\)
このとき原点も通る
よって求める解の個数は
\(\small{ \ k\lt -\displaystyle\frac{2\sqrt{3}}{9} \ }\)のとき\(\small{ \ 1 \ }\)個
\(\small{ \ k=-\displaystyle\frac{2\sqrt{3}}{9} \ }\)のとき\(\small{ \ 2 \ }\)個
\(\small{ \ -\displaystyle\frac{2\sqrt{3}}{9}\lt k\lt 0 \ }\)のとき\(\small{ \ 3 \ }\)個
\(\small{ \ k=0 \ }\)のとき \(\small{ \ 0 \ }\)個
\(\small{ \ k\lt0 \ }\)のとき\(\small{ \ 2 \ }\)個



