こんにちは、リンス(@Lins016)です。
今回は微分の公式について確認しておこう。
微分の公式
数学Ⅲの微分でも数学Ⅱと同じように接線や増減表、最大最小の問題とかいろいろな問題があるんだけど、その前にまずは微分の公式を覚えることから始めないといけないんだ。
数学Ⅱでは\(\small{ \ 3 \ }\)次関数の微分しかなかったから\(\small{ \ (x^3)'=3x^2 \ }\)とかって簡単だったけど、数学Ⅲでは三角関数や指数関数、対数関数、無理関数も微分していくことになる。
だからまずはきちんと微分の公式を覚えておかないといけない。確実に覚えるようにしよう。
・整関数
\(\small{ \ \left(x^n\right)'=nx^{n-1} \ }\)
・積の微分
\(\small{ \ \left(f(x)g(x)\right)'=f'(x)g(x)+f(x)g'(x) \ }\)
・商の微分
\(\small{ \ \left(\displaystyle\frac{f(x)}{g(x)}\right)'=\displaystyle\frac{f'(x)g(x)-f(x)g'(x)}{\left\{g(x)\right\}^2 } \ }\)
・三角関数
\(\small{ \ \left(\sin x\right)'=\cos x \ }\)
\(\small{ \ \left(\cos x\right)'=-\sin x \ }\)
\(\small{ \ \left(\tan x\right)'=\displaystyle\frac{1}{\cos^2 x} \ }\)
・指数関数
\(\small{ \ \left(e^x\right)'=e^x \ }\)
\(\small{ \ \left(a^x\right)=a^x \log a \ }\)
・対数関数
\(\small{ \ \left(\log x\right)'=\displaystyle\frac{1}{x} \ }\)
\(\small{ \ \left(\log_a x\right)'=\displaystyle\frac{1}{x\log a} \ }\)
微分の定義
公式って言っても実際は微分の定義を利用して計算した結果を公式として覚える必要がある。
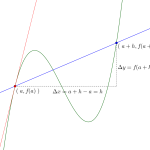
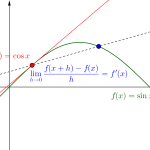
微分の定義って\(\small{ \ f'(x)=\displaystyle \lim_{h\to0}\displaystyle\frac{f(x+h)-f(x)}{h} \ }\)だから、これに代入することで導関数(微分)を求めることができるんだ。
微分の定義についてはこの記事で確認しておこう。
-

微分係数と導関数
平均変化率、微分係数、導関数の違いについて詳しく解説しています。
続きを見る
積と商の微分
\(\small{ \ \left(f(x)g(x)\right)'=f'(x)g(x)+f(x)g'(x) \ }\)
\(\small{ \ \left(\displaystyle\frac{f(x)}{g(x)}\right)'=\displaystyle\frac{f'(x)g(x)-f(x)g'(x)}{\left\{g(x)\right\}^2 } \ }\)
定義を利用した証明も確認しておこう。
-

積と商の導関数(微分)の定義
微分の公式の求め方について詳しく解説しています。
続きを見る
三角関数の微分
\(\small{ \ \left(\sin x\right)'=\cos x \ }\)
\(\small{ \ \left(\cos x\right)'=-\sin x \ }\)
\(\small{ \ \left(\tan x\right)'=\displaystyle\frac{1}{\cos^2 x} \ }\)
定義を利用した証明も確認しておこう。
-

三角関数の微分(導関数)
正弦・余弦・正接の微分について解説しています。
続きを見る
指数関数・対数関数の微分
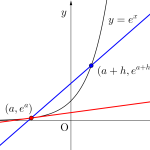
\(\small{ \ \left(e^x\right)'=e^x \ }\)
\(\small{ \ \left(a^x\right)=a^x \log a \ }\)
\(\small{ \ \left(\log x\right)'=\displaystyle\frac{1}{x} \ }\)
\(\small{ \ \left(\log_a x\right)'=\displaystyle\frac{1}{x\log a} \ }\)
定義を利用した証明も確認しておこう。
-

指数関数・対数関数の微分(導関数)
指数関数・対数関数の微分の証明について解説しています。
続きを見る
Point 微分の公式まとめ
①公式を確実に覚える
②定義を利用して求められるようにする