比例式

こんにちは、リンス(@Lins016)です。
今回は比例式について学習していこう。

比例式とは

比例式って聞いたことあるかな？

中学の時に教わる式だけど、高校数学でもよく見かける。\(\small{ \ a:b=x:y \ }\)のように比が等しい式のことを比例式って言うんだ。

これを分数にして\(\small{ \ \displaystyle\frac{a}{b}=\displaystyle\frac{x}{y} \ }\)や\(\small{ \ \displaystyle\frac{a}{x}=\displaystyle\frac{b}{y} \ }\)のように表記する場合もある。

今回はこの比例式について学習していこう。

比例式の内項の積と外項の積

比例式\(\small{ \ a:b=x:y \ }\)は「\(\small{ \ b \ }\)に対する\(\small{ \ a \ }\)の割合と\(\small{ \ y \ }\)に対する\(\small{ \ x \ }\)の割合が等しい」ってことだから、\(\small{ \ \displaystyle\frac{a}{b}=\displaystyle\frac{x}{y} \ }\)が成り立つよね。

両辺を\(\small{ \ by \ }\)倍すると、\(\small{ \ ay=bx \ }\)が言える。

これって中学で教わった、「比例式\(\small{ \ a:b=x:y \ }\)が成り立つとき、内項の積\(\small{ \ bx \ }\)と外項の積\(\small{ \ ay \ }\)が等しい」って式のことだよね。

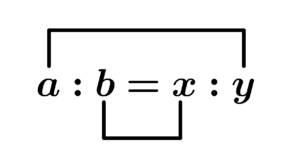
分数型の比例式

比例式\(\small{ \ x:a_1=b_1:b_2 \ }\)が成り立つとき、\(\small{ \ xb_2=a_1b_1 \ }\)から\(\small{ \ x=\displaystyle\frac{a_1b_1}{b_2} \ }\)になるよね。

でもこの式って分数だから計算が複雑になりがち。まぁ、分数のまま計算してもいいんだけど、できるだけ計算が簡単なほうがいいよね。

\(\small{ \ x:a_1=b_1:b_2 \ }\)を\(\small{ \ \displaystyle\frac{x}{a_1}=\displaystyle\frac{b_1}{b_2} \ }\)にして、\(\small{ \ \displaystyle\frac{x}{a_1}=\displaystyle\frac{b_1}{b_2}=k \ }\)とすると、
\(\small{ \ x=ka_1, \ b_1=kb_2 \ }\)になるから、比例式を分数型にして\(\small{ \ k \ }\)とおくことで、分数の計算をなくすことができるんだ。

次の例題を見てみよう。

これを見てわかるけど、解答1では\(\small{ \ a \ }\)を消去して\(\small{ \ b, \ c, \ d \ }\)の三つの文字を利用して解いてるのに対して、解答2では\(\small{ \ b, \ d, \ k \ }\)の三つの文字を利用して解いてるよね。

どちらの解答も三つの文字を利用してるってところは同じだけど、解答1では\(\small{ \ a=\displaystyle\frac{bc}{d} \ }\)って分数の式を代入するから、分母に分数が含まれてる連分数が出てきて計算が大変だよね。

つまり比例式を\(\small{ \ k \ }\)とおくことで計算をなるべく簡単にすることができるってメリットがあるんだ。

だから計算を少しでも少なくするために比例式は分数式にして\(\small{ \ k \ }\)とおこう。

比例式\(\small{ \ a:b=c:d \ }\)は分数式に\(\small{ \ \displaystyle\frac{a}{b}=\displaystyle\frac{c}{d} \ }\)
\(\small{ \ \displaystyle\frac{a}{b}=\displaystyle\frac{c}{d}=k \ }\)とおいて、分母をなくして、\(\small{ \ a=bk, \ c=dk \ }\)を利用しよう。

有名な比例式

高校数学で有名な比例式には正弦定理がある。

正弦定理は分数式\(\small{ \ =k \ }\)じゃなく、 分数式\(\small{ \ =2\mathrm{R} \ }\)ってなってるから気付きにくいし、有名な公式で比例式とは教わっていないかもしれないけど、比例式だよね。

この式も分数型だけど変形すれば
\(\small{ \ a:b:c=\sin \mathrm{A}:\sin\mathrm{B}:\sin \mathrm{C} \ }\)って書くことができるからね。

「\(\small{ \ \sin \mathrm{A}:\sin\mathrm{B}:\sin \mathrm{C}=3:5:7 \ }\)のとき」って言われると「\(\small{ \ a:b:c=3:5:7 \ }\)」から「\(\small{ \ a=3k, \ b=5k, \ c=7k \ }\)」って言えるんだ。

ちなみに三つ以上の比を表したものを連比って言うんだけど、連比は分数型の比例式を\(\small{ \ =k \ }\)とおくとだいぶ計算が楽になる。
だから「連比を見たら\(\small{ \ =k \ }\)とおく」って覚えおこう。

試験に出題される比例式

定期試験でよく出題されるのが、「\(\small{ \ 3^x=4^y=6^z \ (x\neq0) \ }\)のとき、等式\(\small{ \ \displaystyle\frac{1}{x}+\displaystyle\frac{2}{y}=\displaystyle\frac{1}{z} \ }\)を証明せよ」って対数を利用する問題もあるよね。
この場合も\(\small{ \ 3^x=4^y=6^z=k \ }\)とおくと、\(\small{ \ x=\log_3k, \ y=\log_4k, \ z=\log_6k \ }\)ってなるから、一つの文字\(\small{ \ k \ }\)だけで\(\small{ \ x, \ y, \ z \ }\)を表すことができるから、\(\small{ \ k \ }\)を使って証明すればいいよね。

比例式と分数式の値

他にも比例式を使った問題ってある。それは分数型の比例式の値を求めさせる問題。

次の例題を確認して、このタイプの問題を確実に解けるようにしておこう。

定期試験に出題されるような問題だけど、単純に計算するんじゃなくて、どうして\(\small{ \ k \ }\)とおくのか、計算式を楽にする方法は何か？ってことを理解しておかないと、いざ入試で出題されたときに解けないってことになるからね。

\(\small{ \begin{eqnarray}
\left\{
\begin{array}{l}
x+y=zk \\
y+z=xk\\
z+x=yk
\end{array}
\right.
\end{eqnarray} \ }\)
のように循環してる(\(\small{ \ x\to y\to z\to x \ }\))式は辺をそれぞれ加えることで式が対称式になることが多い。
単に文字を消去して計算するのはなかなか大変だから、この方法を知っておくことは大事なことなんだ。

それと\(\small{ \ 2(x+y+z)=k(x+y+z) \ }\)から\(\small{ \ k=2 \ }\)ってやったらまずいよね。\(\small{ \ x+y+z=0 \ }\)なら\(\small{ \ k \ }\)はどんな数でも成り立つからね。

文字で両辺を割る場合は、割る文字が\(\small{ \ 0 \ }\)か\(\small{ \ 0 \ }\)じゃないかで場合分けするか、解答のように移行して因数分解しよう。

Point 比例式

①比例式は分数型にして\(\small{ \ k \ }\)とおく